2022苏科版数学八年级上册 5.2平面直角坐标系课件 (共41张PPT)
文档属性
| 名称 | 2022苏科版数学八年级上册 5.2平面直角坐标系课件 (共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 10:50:44 | ||
图片预览











文档简介
(共41张PPT)
平面直角坐标系
平面直角坐标系与点坐标
目录
1
2
3
用割补法求面积
坐标系中点的变换
平面直角坐标系与点坐标
目录
1
2
3
坐标系中点的变换
用割补法求面积
讲解
引入
例题
练习
总结
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
实数和数轴
一个数确定点的位置
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
两个数确定点的位置
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
有序数对
(a, b)
(b, a)
电影院的2排3座—(2,3)
电影院的3排2座—(3,2)
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
y
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y轴或纵轴
原点
①两条数轴
②互相垂直
③公共原点
平面直角坐标系
平面内两条互相垂直、原点重合的数轴
平面直角坐标系与点坐标
x轴或横轴
讲解
引入
例题
练习
总结
象限
y
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
第二象限
第一象限
第三象限
第四象限
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
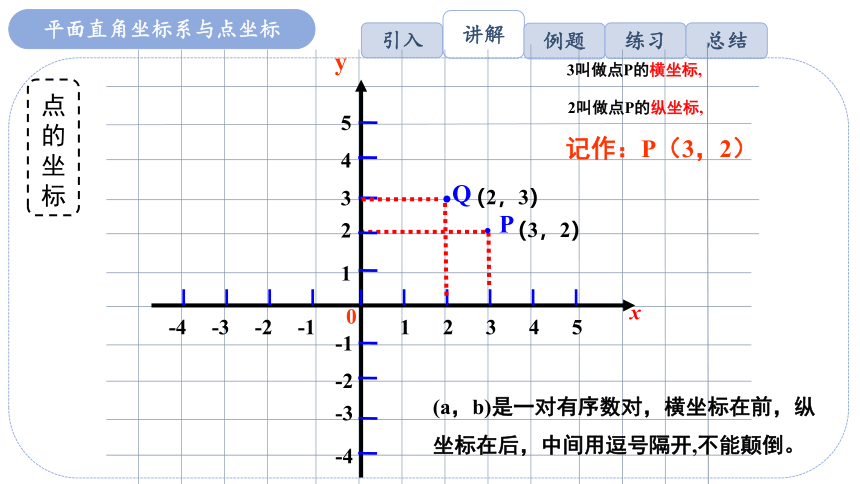
(3,2)
P
y
3叫做点P的横坐标,
2叫做点P的纵坐标,
x
记作:P(3,2)
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
.Q
(2,3)
(a,b)是一对有序数对,横坐标在前,纵
坐标在后,中间用逗号隔开,不能颠倒。
点的坐标
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
点的坐标
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
·
平面直角坐标系与点坐标
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
讲解
引入
例题
练习
总结
·
B
x
横轴
y
纵轴
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -3,- 3 )
( 1,- 2 )
·
(-,+)
(-,-)
象限内点的坐标特点
·
·
·
平面直角坐标系与点坐标
( + ,- )
( + ,+)
讲解
引入
例题
练习
总结
象限内点的坐标特点
第一象限(正,正) 第二象限(负,正)
第三象限(负,负)
第四象限(正,负)
横轴(x轴)上的点:y=0
纵轴(y轴)上的点:x=0
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
79
讲解
引入
练习
例题
总结
79
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
79
讲解
引入
练习
例题
总结
79
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
80
讲解
引入
练习
例题
总结
80
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
80
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
80
讲解
引入
例题
练习
总结
坐标系中点的变换
1
2
3
4
-3
-2
-1
O
1
2
3
y
-3
-2
-1
x
P (1, -3)
A (2, 3)
●
●
A到x轴的距离为3
到y轴的距离为2
P到x轴的距离为3
到y轴的距离为1
P(x,y)到x轴的距离为|y|
到y轴的距离为|x|
点坐标的几何意义
讲解
引入
例题
练习
总结
坐标系中点的变换
补充
平面直角坐标系与点坐标
目录
1
2
3
坐标系中点的变换
用割补法求面积
讲解
引入
例题
练习
总结
坐标系中点的变换
1
2
3
4
-3
-2
-1
O
1
2
3
y
-3
-2
-1
x
●
●
●
●
●
A (1, 2)
(1+2, 2)
(1, 2+2)
(1-3, 2)
(1, 2-3)
讲解
引入
例题
练习
总结
坐标系中点的变换
讲解
引入
例题
练习
总结
坐标系中点的变换
82
讲解
引入
练习
例题
总结
82
坐标系中点的变换
讲解
引入
例题
练习
总结
坐标系中点的变换
82
讲解
引入
练习
例题
总结
82
坐标系中点的变换
讲解
引入
例题
练习
总结
坐标系中点的变换
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
( 2,3 )
A1(2,-3)
A2(-2,3)
A3(-2,-3)
讲解
引入
例题
练习
总结
坐标系中点的变换
总结
已知点A(m,n)
则A点关于x轴的对称点为(m,-n)
则A点关于y轴的对称点为(-m,n)
则A点关于原点的对称点为(-m,-n)
讲解
引入
例题
练习
总结
坐标系中点的变换
83
讲解
引入
练习
例题
总结
83
坐标系中点的变换
讲解
引入
例题
练习
总结
83
坐标系中点的变换
讲解
引入
例题
练习
总结
84
坐标系中点的变换
平面直角坐标系与点坐标
目录
1
2
3
用割补法求面积
坐标系中点的变换
讲解
引入
例题
练习
总结
用割补法求面积
86
讲解
引入
练习
例题
总结
86
用割补法求面积
讲解
引入
例题
练习
总结
86
用割补法求面积
讲解
引入
例题
练习
总结
87
用割补法求面积
明天见!
平面直角坐标系
平面直角坐标系与点坐标
目录
1
2
3
用割补法求面积
坐标系中点的变换
平面直角坐标系与点坐标
目录
1
2
3
坐标系中点的变换
用割补法求面积
讲解
引入
例题
练习
总结
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
实数和数轴
一个数确定点的位置
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
两个数确定点的位置
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
有序数对
(a, b)
(b, a)
电影院的2排3座—(2,3)
电影院的3排2座—(3,2)
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
y
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y轴或纵轴
原点
①两条数轴
②互相垂直
③公共原点
平面直角坐标系
平面内两条互相垂直、原点重合的数轴
平面直角坐标系与点坐标
x轴或横轴
讲解
引入
例题
练习
总结
象限
y
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
第二象限
第一象限
第三象限
第四象限
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
(3,2)
P
y
3叫做点P的横坐标,
2叫做点P的纵坐标,
x
记作:P(3,2)
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
.Q
(2,3)
(a,b)是一对有序数对,横坐标在前,纵
坐标在后,中间用逗号隔开,不能颠倒。
点的坐标
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
点的坐标
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
·
平面直角坐标系与点坐标
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
讲解
引入
例题
练习
总结
·
B
x
横轴
y
纵轴
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -3,- 3 )
( 1,- 2 )
·
(-,+)
(-,-)
象限内点的坐标特点
·
·
·
平面直角坐标系与点坐标
( + ,- )
( + ,+)
讲解
引入
例题
练习
总结
象限内点的坐标特点
第一象限(正,正) 第二象限(负,正)
第三象限(负,负)
第四象限(正,负)
横轴(x轴)上的点:y=0
纵轴(y轴)上的点:x=0
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
79
讲解
引入
练习
例题
总结
79
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
79
讲解
引入
练习
例题
总结
79
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
80
讲解
引入
练习
例题
总结
80
平面直角坐标系与点坐标
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
80
讲解
引入
例题
练习
总结
平面直角坐标系与点坐标
80
讲解
引入
例题
练习
总结
坐标系中点的变换
1
2
3
4
-3
-2
-1
O
1
2
3
y
-3
-2
-1
x
P (1, -3)
A (2, 3)
●
●
A到x轴的距离为3
到y轴的距离为2
P到x轴的距离为3
到y轴的距离为1
P(x,y)到x轴的距离为|y|
到y轴的距离为|x|
点坐标的几何意义
讲解
引入
例题
练习
总结
坐标系中点的变换
补充
平面直角坐标系与点坐标
目录
1
2
3
坐标系中点的变换
用割补法求面积
讲解
引入
例题
练习
总结
坐标系中点的变换
1
2
3
4
-3
-2
-1
O
1
2
3
y
-3
-2
-1
x
●
●
●
●
●
A (1, 2)
(1+2, 2)
(1, 2+2)
(1-3, 2)
(1, 2-3)
讲解
引入
例题
练习
总结
坐标系中点的变换
讲解
引入
例题
练习
总结
坐标系中点的变换
82
讲解
引入
练习
例题
总结
82
坐标系中点的变换
讲解
引入
例题
练习
总结
坐标系中点的变换
82
讲解
引入
练习
例题
总结
82
坐标系中点的变换
讲解
引入
例题
练习
总结
坐标系中点的变换
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
( 2,3 )
A1(2,-3)
A2(-2,3)
A3(-2,-3)
讲解
引入
例题
练习
总结
坐标系中点的变换
总结
已知点A(m,n)
则A点关于x轴的对称点为(m,-n)
则A点关于y轴的对称点为(-m,n)
则A点关于原点的对称点为(-m,-n)
讲解
引入
例题
练习
总结
坐标系中点的变换
83
讲解
引入
练习
例题
总结
83
坐标系中点的变换
讲解
引入
例题
练习
总结
83
坐标系中点的变换
讲解
引入
例题
练习
总结
84
坐标系中点的变换
平面直角坐标系与点坐标
目录
1
2
3
用割补法求面积
坐标系中点的变换
讲解
引入
例题
练习
总结
用割补法求面积
86
讲解
引入
练习
例题
总结
86
用割补法求面积
讲解
引入
例题
练习
总结
86
用割补法求面积
讲解
引入
例题
练习
总结
87
用割补法求面积
明天见!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
