人教版八年级上册13.3等腰三角形 课件(共21张PPT)
文档属性
| 名称 | 人教版八年级上册13.3等腰三角形 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 08:32:27 | ||
图片预览







文档简介
(共21张PPT)
13.3 等腰三角形
等腰三角形
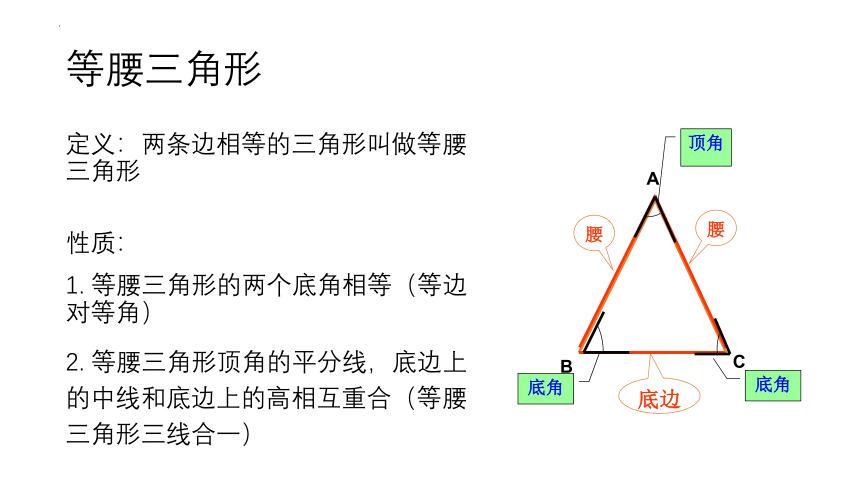
定义:两条边相等的三角形叫做等腰三角形
性质:
1. 等腰三角形的两个底角相等(等边对等角)
2. 等腰三角形顶角的平分线,底边上的中线和底边上的高相互重合(等腰三角形三线合一)
A
B
C
腰
腰
底边
顶角
底角
底角
等腰三角形性质数学表示
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD ,AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD ,AD为顶角平分线
C
A
B
D
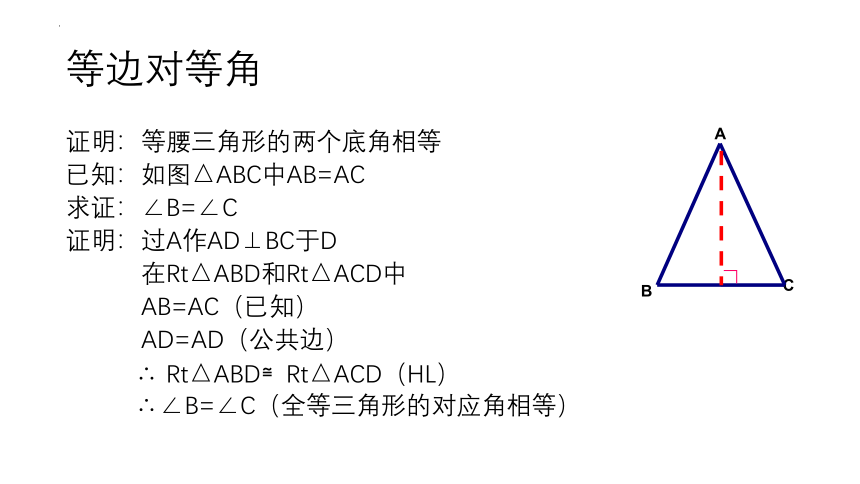
等边对等角
证明:等腰三角形的两个底角相等
已知:如图△ABC中AB=AC
求证:∠B=∠C
证明:过A作AD⊥BC于D
在Rt△ABD和Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ABD≌Rt△ACD(HL)
∴∠B=∠C(全等三角形的对应角相等)
C
A
B
∟
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
等边三角形
定义:三条边都相等的三角形叫做等边三角形
性质:
边的性质:三边都相等
角的性质: 三个内角都相等,并且每一个角都等于60°.
对称性:等边三角形是轴对称图形,它有三条对称轴。
“三线合一”:等边三角形一个角的平分线与对边上的高线、中线互相重合。
等边三角形的判定
判定1: 三个角都相等的三角形是等边三角形。
判定2: 有一个角是 60°的等腰三角形是等边三角形。
判定3:三边相等的三角形是等边三角形。
等边三角形与等腰三角形活动
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
用法归纳
等腰三角形的判定方法有下列几种:1定义 2判定定理
等边三角形的判定方法有以下几种:1定义 2判定1 3判定2
等腰三角形的判定定理与性质定理的区别是条件和结论刚好相反
运用等腰三角形的判定定理时,应注意在同一个三角形中
含30 °直角三角形定理
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
小结
1. 判断
(1)等腰三角形的角平分线、中线和高互相重合( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°( )
(3)等腰三角形的底角都是锐角 ( )
(4)钝角三角形不可能是等腰三角形 ( )
2.三边都相等的三角形叫做____三角形.
3.等边三角形的每个内角都等于____度.
4.等边三角形有____条对称轴.
5.等边三角形的对称轴的交点叫___.
等边三角形绕中心至少旋转___度.才能和原来的三角形重合.
6. 如图1,正方形ABCD的边BC、CD上取E、F两点,使∠EAF=45°,AG⊥EF于G.
7. 如图2,在△ABC中,AB=AC,P是三角形内任意一点,∠APB=∠APC.
8. 等腰三角形的一边等于5,一边等于12,则它的周长为( )
A.22 B.29 C.22或29 D.17
9. 在△ABC中,∠A和∠B的度数如下,其中能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
10. 如图14-111所示,在△ABC中,AB=AC,BD是角平分线,若∠BDC=69°,则∠A等于( )
A.32° B.36° C.48° D.52°
11. 等腰三角形的一个内角等于130°,则其余两个角分别为 ;
12. 等腰三角形的一个内角等于70°,则其余两个角分别为 .
13. 如图14-112所示,△ABC是等边三角形,∠1=∠2=∠3,求∠BEC的度数.
14.如图14-113所示,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.
15. 如图14-114所示,在△ABC中,点E在AC上,点N在BC上,在AB上找一点F,使△ENF的周长最小,试说明理由.
16. 等腰三角形的两边长分别为4cm和9cm,则它的周长为 .
17. 等腰三角形一腰上的高与底边的夹角为35°,则这个三角形的顶角为 .
18. 在△ABC中,AB=AC,∠A+∠B=140°,则∠A= .
19. 如果等腰三角形的两个角的比是2∶5,那么底角的度数=?
20. 如图14-117所示,在△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=3,BD=5,则点D到AB的距离为 .
21. 如图14-118所示,在△ABC中,AB=AC,∠A=60°,BE⊥AC于E,延长BC到D,使CD=CE,连接DE,若△ABC的周长是24,BE=a,则△BDE的周长是 .
22. 如图14-119所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.
23. 如图14-120所示,在△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到E点,使BE=BD,过点D,E引直线交AC于点F,则有AF=FC,为什么?
13.3 等腰三角形
等腰三角形
定义:两条边相等的三角形叫做等腰三角形
性质:
1. 等腰三角形的两个底角相等(等边对等角)
2. 等腰三角形顶角的平分线,底边上的中线和底边上的高相互重合(等腰三角形三线合一)
A
B
C
腰
腰
底边
顶角
底角
底角
等腰三角形性质数学表示
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD ,AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD ,AD为顶角平分线
C
A
B
D
等边对等角
证明:等腰三角形的两个底角相等
已知:如图△ABC中AB=AC
求证:∠B=∠C
证明:过A作AD⊥BC于D
在Rt△ABD和Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ABD≌Rt△ACD(HL)
∴∠B=∠C(全等三角形的对应角相等)
C
A
B
∟
等腰三角形的判定定理
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简写成:等角对等边
等边三角形
定义:三条边都相等的三角形叫做等边三角形
性质:
边的性质:三边都相等
角的性质: 三个内角都相等,并且每一个角都等于60°.
对称性:等边三角形是轴对称图形,它有三条对称轴。
“三线合一”:等边三角形一个角的平分线与对边上的高线、中线互相重合。
等边三角形的判定
判定1: 三个角都相等的三角形是等边三角形。
判定2: 有一个角是 60°的等腰三角形是等边三角形。
判定3:三边相等的三角形是等边三角形。
等边三角形与等腰三角形活动
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
用法归纳
等腰三角形的判定方法有下列几种:1定义 2判定定理
等边三角形的判定方法有以下几种:1定义 2判定1 3判定2
等腰三角形的判定定理与性质定理的区别是条件和结论刚好相反
运用等腰三角形的判定定理时,应注意在同一个三角形中
含30 °直角三角形定理
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
小结
1. 判断
(1)等腰三角形的角平分线、中线和高互相重合( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°( )
(3)等腰三角形的底角都是锐角 ( )
(4)钝角三角形不可能是等腰三角形 ( )
2.三边都相等的三角形叫做____三角形.
3.等边三角形的每个内角都等于____度.
4.等边三角形有____条对称轴.
5.等边三角形的对称轴的交点叫___.
等边三角形绕中心至少旋转___度.才能和原来的三角形重合.
6. 如图1,正方形ABCD的边BC、CD上取E、F两点,使∠EAF=45°,AG⊥EF于G.
7. 如图2,在△ABC中,AB=AC,P是三角形内任意一点,∠APB=∠APC.
8. 等腰三角形的一边等于5,一边等于12,则它的周长为( )
A.22 B.29 C.22或29 D.17
9. 在△ABC中,∠A和∠B的度数如下,其中能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
10. 如图14-111所示,在△ABC中,AB=AC,BD是角平分线,若∠BDC=69°,则∠A等于( )
A.32° B.36° C.48° D.52°
11. 等腰三角形的一个内角等于130°,则其余两个角分别为 ;
12. 等腰三角形的一个内角等于70°,则其余两个角分别为 .
13. 如图14-112所示,△ABC是等边三角形,∠1=∠2=∠3,求∠BEC的度数.
14.如图14-113所示,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.
15. 如图14-114所示,在△ABC中,点E在AC上,点N在BC上,在AB上找一点F,使△ENF的周长最小,试说明理由.
16. 等腰三角形的两边长分别为4cm和9cm,则它的周长为 .
17. 等腰三角形一腰上的高与底边的夹角为35°,则这个三角形的顶角为 .
18. 在△ABC中,AB=AC,∠A+∠B=140°,则∠A= .
19. 如果等腰三角形的两个角的比是2∶5,那么底角的度数=?
20. 如图14-117所示,在△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=3,BD=5,则点D到AB的距离为 .
21. 如图14-118所示,在△ABC中,AB=AC,∠A=60°,BE⊥AC于E,延长BC到D,使CD=CE,连接DE,若△ABC的周长是24,BE=a,则△BDE的周长是 .
22. 如图14-119所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.
23. 如图14-120所示,在△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到E点,使BE=BD,过点D,E引直线交AC于点F,则有AF=FC,为什么?
