2022苏科版初中数学八年级上册 3勾股定理提升课件(共79张PPT)
文档属性
| 名称 | 2022苏科版初中数学八年级上册 3勾股定理提升课件(共79张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 07:22:58 | ||
图片预览









文档简介
(共79张PPT)
勾股定理
目录
1
2
3
探究与验证
勾股定理的计算
勾股定理逆定理
勾股定理的应用
4
目录
1
探究与验证
引入
讲解
例题
练习
总结
1.菱形的性质
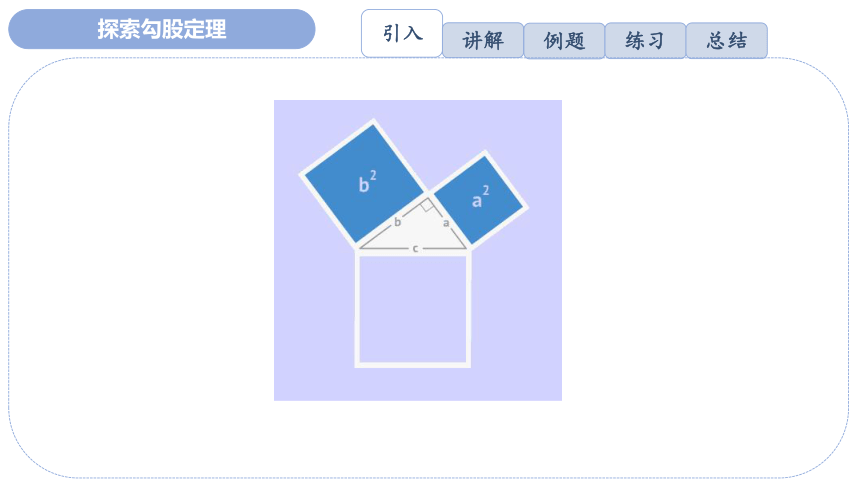
探索勾股定理
引入
讲解
例题
练习
总结
探索勾股定理
引入
讲解
例题
练习
总结
勾股定理的发现
在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯,他用演绎法证明了勾股定理
引入
讲解
例题
练习
总结
勾股定理的发现
在中国,公元前1000年商朝的商高提出了“勾三股四玄五”的勾股定理的特例.
公元前1世纪,《周髀算经》记载了商高所提供的测量方法是
“勾股术”:“故折矩,以为勾广三,股修四,径隅五。”什么意思呢?
引入
讲解
例题
练习
总结
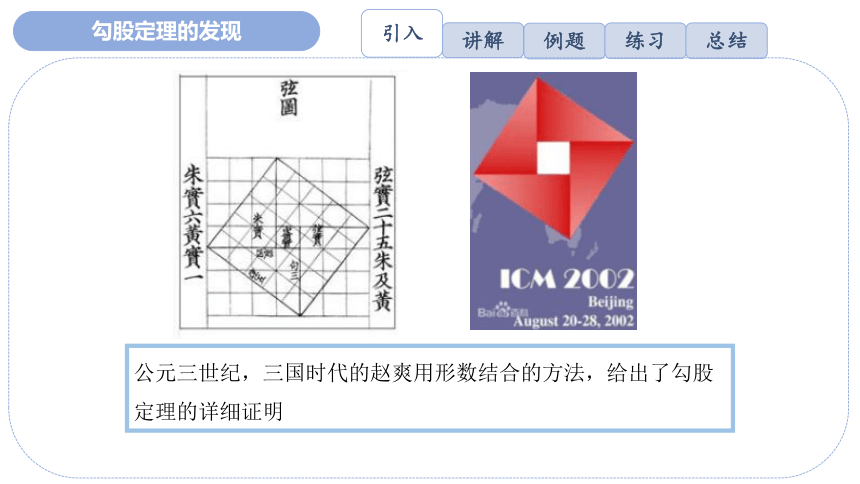
勾股定理的发现
公元三世纪,三国时代的赵爽用形数结合的方法,给出了勾股定理的详细证明
引入
讲解
例题
练习
总结
勾股定理的定义
勾股定理内容:
直角三角形中,两直角边平方之和等于斜边的平方。
数学语言: 在直角三角形中,∠C=90°
引入
讲解
例题
练习
总结
勾股定理的验证
1.1 网格图中验证
1.2 图形分割验证
引入
讲解
例题
练习
总结
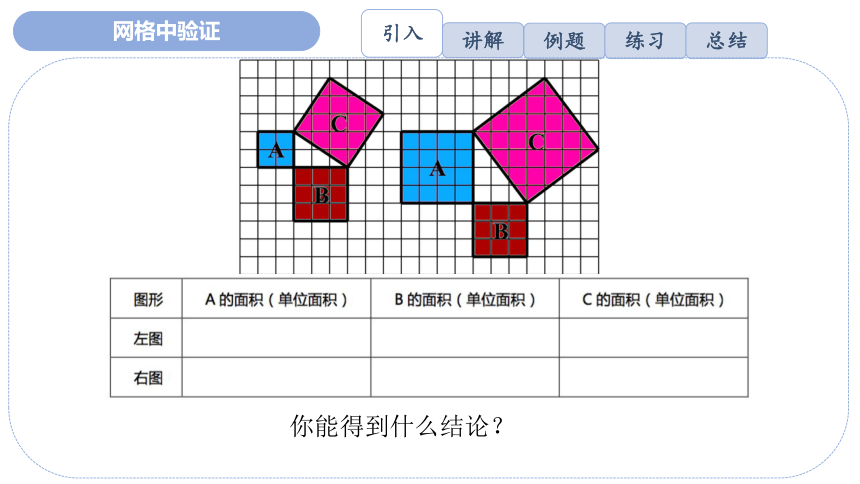
网格中验证
你能得到什么结论?
引入
讲解
例题
练习
总结
勾股定理的验证
1.1 网格图中验证
1.2 图形分割验证
引入
讲解
例题
练习
总结
图形分割验证
毕达哥拉斯图
赵爽弦图
总统图
引入
讲解
例题
练习
总结
图形分割验证
毕达哥拉斯图
整体:正方形
等量关系:
a
a
a
a
b
b
b
b
c
c
c
c
部分:四个三角形
+
一个正方形
引入
讲解
例题
练习
总结
图形分割验证
赵爽弦图
整体:正方形
部分:四个三角形
+
一个正方形
等量关系:
引入
讲解
例题
练习
总结
图形分割验证
b
c
a
b
c
a
整体:梯形
部分:三个直角三角形的和
等量关系:
引入
讲解
例题
练习
总结
勾股定理的定义
总结:图形分割验证的步骤
①表示整体面积
②表示部分面积
③建立等量关系:整体面积=部分面积之和
引入
讲解
例题
练习
总结
勾股树
引入
讲解
例题
练习
总结
勾股树
勾股树:又称毕达哥拉斯树,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形,因为重复数次后的形状好似一棵树而得名.
目录
2
勾股定理逆定理
讲解
引入
例题
练习
总结
逆定理
若 或
△ABC仍然是直角三角形吗?
直角是哪个角呢?
讲解
引入
例题
练习
总结
逆定理
勾股定理的逆定理
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对角为直角.
特别说明:
A
C
B
a
b
c
数学语言:在△ABC中,如果 a2+b2=c2 ,那么,∠C=90°
讲解
引入
例题
练习
总结
勾股定理逆定理
1
2
根据三边长判断三角形形状
勾股数
根据数量关系判断三角形形状
综合
3
4
讲解
引入
例题
练习
总结
综合应用
1
2
3
4
根据三边长判断三角形形状
讲解
引入
例题
练习
总结
根据三边长判断三角形形状
72
讲解
引入
练习
例题
总结
根据三边长判断三角形形状
72
讲解
引入
例题
练习
总结
根据数量关系判断三角形形状
2
2
3
4
根据数量关系判断三角形形状
讲解
引入
例题
练习
总结
根据数量关系判断三角形形状
73
讲解
引入
练习
例题
总结
根据数量关系判断三角形形状
73
讲解
引入
思考
例题
总结
根据数量关系判断三角形形状
77
若出现a2+b2<c2及a2+b2>c2,则分别为什么三角形呢?
A
B
C
b
c
B
a2+b2<c2,为钝角三角形
a
讲解
引入
思考
例题
总结
根据数量关系判断三角形形状
77
若出现a2+b2<c2及a2+b2>c2,则分别为什么三角形呢?
B
C
a
b
a2+b2>c2为锐角三角形
B
a
A
讲解
引入
例题
练习
总结
勾股数
3
2
3
4
勾股数
讲解
引入
例题
练习
总结
勾股数
72
讲解
引入
练习
例题
总结
勾股数
73
讲解
引入
例题
练习
总结
综合应用
4
2
3
4
综合
讲解
引入
例题
练习
总结
计算图形的面积
74
求一个不规则四边形的面积
已知:一个直角+四条边
做法:1.利用直角构造直角三角形
2.根据勾股定理逆定理确定直角三角形
3.再利用面积间关系求出四边形面积
讲解
引入
练习
例题
总结
计算图形的面积
74
目录
3
勾股定理的应用
讲解
引入
例题
练习
总结
勾股定理的应用
1
2
利用勾股定理解决实际问题
立方体表面最短路径问题
方程思想(折叠问题)
全等三角形与勾股定理综合
3
4
讲解
引入
例题
练习
总结
勾股定理的应用
1
2
利用勾股定理解决实际问题
3
4
讲解
引入
例题
练习
总结
76
讲解
引入
练习
例题
总结
76
讲解
引入
例题
练习
总结
勾股定理的应用
2
2
3
4
方程思想(折叠问题)
讲解
引入
例题
练习
总结
方程思想
应用:1.生活:(旗杆、芦苇、猴子爬树)
2.折叠问题:(三角形中、长方形中)
在一个直角三角形中,已知一边与另外两边的数量关系,可设其中
一边为x,利用勾股定理列方程求解.
讲解
引入
例题
练习
总结
方程思想
76
讲解
引入
练习
例题
总结
方程思想
77
讲解
引入
练习
例题
总结
方程思想
补
【旗杆问题】
讲解
引入
例题
练习
总结
方程思想
折叠问题中的基本结论:
对应边相等
对应角相等
折痕所在的直线相当于角平分线
折痕所在的直线相当于对称轴
折痕所在直线是对应点连线的垂直平分线
讲解
引入
例题
练习
总结
方程思想
77
讲解
引入
练习
例题
总结
方程思想
77
讲解
引入
练习
例题
总结
方程思想
77
讲解
引入
例题
练习
总结
方程思想
补
讲解
引入
例题
练习
总结
方程思想
补
讲解
引入
例题
练习
总结
勾股定理的应用
3
2
3
4
立方体表面最短路径问题
讲解
引入
例题
练习
总结
圆柱体表面的最短路径
78
【经典例题】
讲解
引入
例题
练习
总结
立方体表面的最短距离
78
1.如图,在棱长为1的正方体的表面上,求从顶点A到顶点C’的最短距离的平方.
【经典例题】
A
C’
C
D
B
B’
C’
D’
A’
B
A
B’
A
C’
B
C
B’
A’
前+右
前+上
右+下
画立体图形的平面展开图,在展开图中标示字母
讲解
引入
例题
练习
总结
78
讲解
引入
练习
例题
总结
补
A
G
4
4
D
C
D’
E
讲解
引入
总结
例题
练习
最短路径原理和方法
求最短路径的原理:
①两点之间线段最短;②垂线段最短.
具体方法:
(1)画平面展开图(长方体为三种展开图:①前(后)+左(右);②前(后)+上(下);③左(右)+上(下));
(2)正确标示字母;
(3)找直角列勾股(长方体找最小值可以用“和同差大积小”).
讲解
引入
例题
练习
总结
综合应用
4
2
3
4
全等三角形与勾股定理综合
讲解
引入
例题
练习
总结
综合
79
讲解
引入
例题
练习
总结
综合
79
讲解
引入
例题
练习
总结
综合
79
讲解
引入
练习
例题
总结
综合
80
目录
4
计算
讲解
引入
例题
练习
总结
概念表述
直角三角形两直角边的平方和等于斜边的平方。
a
A
C
B
b
c
如图所示,a,b,c分别表示直角三角形的两直角边和斜边,那么:
讲解
引入
例题
练习
总结
概念表述
a
C
A
B
b
c
a
C
A
B
b
c
1.前提必须是在直角三角形中;
2.斜边和直角必须说明白
讲解
引入
例题
练习
总结
常见的勾股数
勾股数:需满足 ①a2+b2=c2 ②正整数
讲解
引入
例题
练习
总结
计算
66
讲解
引入
练习
例题
总结
计算
66
讲解
引入
练习
例题
总结
计算
66
讲解
引入
练习
例题
总结
计算
补
讲解
引入
例题
练习
总结
利用勾股定理解决实际问题
67
Rt
讲解
引入
练习
例题
总结
含特殊角的三角形
67
讲解
引入
例题
练习
总结
含特殊角的三角形
67
讲解
引入
练习
例题
总结
含特殊角的三角形
68
讲解
引入
例题
练习
总结
68
讲解
引入
练习
例题
总结
68
明天见!
勾股定理
目录
1
2
3
探究与验证
勾股定理的计算
勾股定理逆定理
勾股定理的应用
4
目录
1
探究与验证
引入
讲解
例题
练习
总结
1.菱形的性质
探索勾股定理
引入
讲解
例题
练习
总结
探索勾股定理
引入
讲解
例题
练习
总结
勾股定理的发现
在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯,他用演绎法证明了勾股定理
引入
讲解
例题
练习
总结
勾股定理的发现
在中国,公元前1000年商朝的商高提出了“勾三股四玄五”的勾股定理的特例.
公元前1世纪,《周髀算经》记载了商高所提供的测量方法是
“勾股术”:“故折矩,以为勾广三,股修四,径隅五。”什么意思呢?
引入
讲解
例题
练习
总结
勾股定理的发现
公元三世纪,三国时代的赵爽用形数结合的方法,给出了勾股定理的详细证明
引入
讲解
例题
练习
总结
勾股定理的定义
勾股定理内容:
直角三角形中,两直角边平方之和等于斜边的平方。
数学语言: 在直角三角形中,∠C=90°
引入
讲解
例题
练习
总结
勾股定理的验证
1.1 网格图中验证
1.2 图形分割验证
引入
讲解
例题
练习
总结
网格中验证
你能得到什么结论?
引入
讲解
例题
练习
总结
勾股定理的验证
1.1 网格图中验证
1.2 图形分割验证
引入
讲解
例题
练习
总结
图形分割验证
毕达哥拉斯图
赵爽弦图
总统图
引入
讲解
例题
练习
总结
图形分割验证
毕达哥拉斯图
整体:正方形
等量关系:
a
a
a
a
b
b
b
b
c
c
c
c
部分:四个三角形
+
一个正方形
引入
讲解
例题
练习
总结
图形分割验证
赵爽弦图
整体:正方形
部分:四个三角形
+
一个正方形
等量关系:
引入
讲解
例题
练习
总结
图形分割验证
b
c
a
b
c
a
整体:梯形
部分:三个直角三角形的和
等量关系:
引入
讲解
例题
练习
总结
勾股定理的定义
总结:图形分割验证的步骤
①表示整体面积
②表示部分面积
③建立等量关系:整体面积=部分面积之和
引入
讲解
例题
练习
总结
勾股树
引入
讲解
例题
练习
总结
勾股树
勾股树:又称毕达哥拉斯树,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形,因为重复数次后的形状好似一棵树而得名.
目录
2
勾股定理逆定理
讲解
引入
例题
练习
总结
逆定理
若 或
△ABC仍然是直角三角形吗?
直角是哪个角呢?
讲解
引入
例题
练习
总结
逆定理
勾股定理的逆定理
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对角为直角.
特别说明:
A
C
B
a
b
c
数学语言:在△ABC中,如果 a2+b2=c2 ,那么,∠C=90°
讲解
引入
例题
练习
总结
勾股定理逆定理
1
2
根据三边长判断三角形形状
勾股数
根据数量关系判断三角形形状
综合
3
4
讲解
引入
例题
练习
总结
综合应用
1
2
3
4
根据三边长判断三角形形状
讲解
引入
例题
练习
总结
根据三边长判断三角形形状
72
讲解
引入
练习
例题
总结
根据三边长判断三角形形状
72
讲解
引入
例题
练习
总结
根据数量关系判断三角形形状
2
2
3
4
根据数量关系判断三角形形状
讲解
引入
例题
练习
总结
根据数量关系判断三角形形状
73
讲解
引入
练习
例题
总结
根据数量关系判断三角形形状
73
讲解
引入
思考
例题
总结
根据数量关系判断三角形形状
77
若出现a2+b2<c2及a2+b2>c2,则分别为什么三角形呢?
A
B
C
b
c
B
a2+b2<c2,为钝角三角形
a
讲解
引入
思考
例题
总结
根据数量关系判断三角形形状
77
若出现a2+b2<c2及a2+b2>c2,则分别为什么三角形呢?
B
C
a
b
a2+b2>c2为锐角三角形
B
a
A
讲解
引入
例题
练习
总结
勾股数
3
2
3
4
勾股数
讲解
引入
例题
练习
总结
勾股数
72
讲解
引入
练习
例题
总结
勾股数
73
讲解
引入
例题
练习
总结
综合应用
4
2
3
4
综合
讲解
引入
例题
练习
总结
计算图形的面积
74
求一个不规则四边形的面积
已知:一个直角+四条边
做法:1.利用直角构造直角三角形
2.根据勾股定理逆定理确定直角三角形
3.再利用面积间关系求出四边形面积
讲解
引入
练习
例题
总结
计算图形的面积
74
目录
3
勾股定理的应用
讲解
引入
例题
练习
总结
勾股定理的应用
1
2
利用勾股定理解决实际问题
立方体表面最短路径问题
方程思想(折叠问题)
全等三角形与勾股定理综合
3
4
讲解
引入
例题
练习
总结
勾股定理的应用
1
2
利用勾股定理解决实际问题
3
4
讲解
引入
例题
练习
总结
76
讲解
引入
练习
例题
总结
76
讲解
引入
例题
练习
总结
勾股定理的应用
2
2
3
4
方程思想(折叠问题)
讲解
引入
例题
练习
总结
方程思想
应用:1.生活:(旗杆、芦苇、猴子爬树)
2.折叠问题:(三角形中、长方形中)
在一个直角三角形中,已知一边与另外两边的数量关系,可设其中
一边为x,利用勾股定理列方程求解.
讲解
引入
例题
练习
总结
方程思想
76
讲解
引入
练习
例题
总结
方程思想
77
讲解
引入
练习
例题
总结
方程思想
补
【旗杆问题】
讲解
引入
例题
练习
总结
方程思想
折叠问题中的基本结论:
对应边相等
对应角相等
折痕所在的直线相当于角平分线
折痕所在的直线相当于对称轴
折痕所在直线是对应点连线的垂直平分线
讲解
引入
例题
练习
总结
方程思想
77
讲解
引入
练习
例题
总结
方程思想
77
讲解
引入
练习
例题
总结
方程思想
77
讲解
引入
例题
练习
总结
方程思想
补
讲解
引入
例题
练习
总结
方程思想
补
讲解
引入
例题
练习
总结
勾股定理的应用
3
2
3
4
立方体表面最短路径问题
讲解
引入
例题
练习
总结
圆柱体表面的最短路径
78
【经典例题】
讲解
引入
例题
练习
总结
立方体表面的最短距离
78
1.如图,在棱长为1的正方体的表面上,求从顶点A到顶点C’的最短距离的平方.
【经典例题】
A
C’
C
D
B
B’
C’
D’
A’
B
A
B’
A
C’
B
C
B’
A’
前+右
前+上
右+下
画立体图形的平面展开图,在展开图中标示字母
讲解
引入
例题
练习
总结
78
讲解
引入
练习
例题
总结
补
A
G
4
4
D
C
D’
E
讲解
引入
总结
例题
练习
最短路径原理和方法
求最短路径的原理:
①两点之间线段最短;②垂线段最短.
具体方法:
(1)画平面展开图(长方体为三种展开图:①前(后)+左(右);②前(后)+上(下);③左(右)+上(下));
(2)正确标示字母;
(3)找直角列勾股(长方体找最小值可以用“和同差大积小”).
讲解
引入
例题
练习
总结
综合应用
4
2
3
4
全等三角形与勾股定理综合
讲解
引入
例题
练习
总结
综合
79
讲解
引入
例题
练习
总结
综合
79
讲解
引入
例题
练习
总结
综合
79
讲解
引入
练习
例题
总结
综合
80
目录
4
计算
讲解
引入
例题
练习
总结
概念表述
直角三角形两直角边的平方和等于斜边的平方。
a
A
C
B
b
c
如图所示,a,b,c分别表示直角三角形的两直角边和斜边,那么:
讲解
引入
例题
练习
总结
概念表述
a
C
A
B
b
c
a
C
A
B
b
c
1.前提必须是在直角三角形中;
2.斜边和直角必须说明白
讲解
引入
例题
练习
总结
常见的勾股数
勾股数:需满足 ①a2+b2=c2 ②正整数
讲解
引入
例题
练习
总结
计算
66
讲解
引入
练习
例题
总结
计算
66
讲解
引入
练习
例题
总结
计算
66
讲解
引入
练习
例题
总结
计算
补
讲解
引入
例题
练习
总结
利用勾股定理解决实际问题
67
Rt
讲解
引入
练习
例题
总结
含特殊角的三角形
67
讲解
引入
例题
练习
总结
含特殊角的三角形
67
讲解
引入
练习
例题
总结
含特殊角的三角形
68
讲解
引入
例题
练习
总结
68
讲解
引入
练习
例题
总结
68
明天见!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
