反比例函数复习课件[上学期]

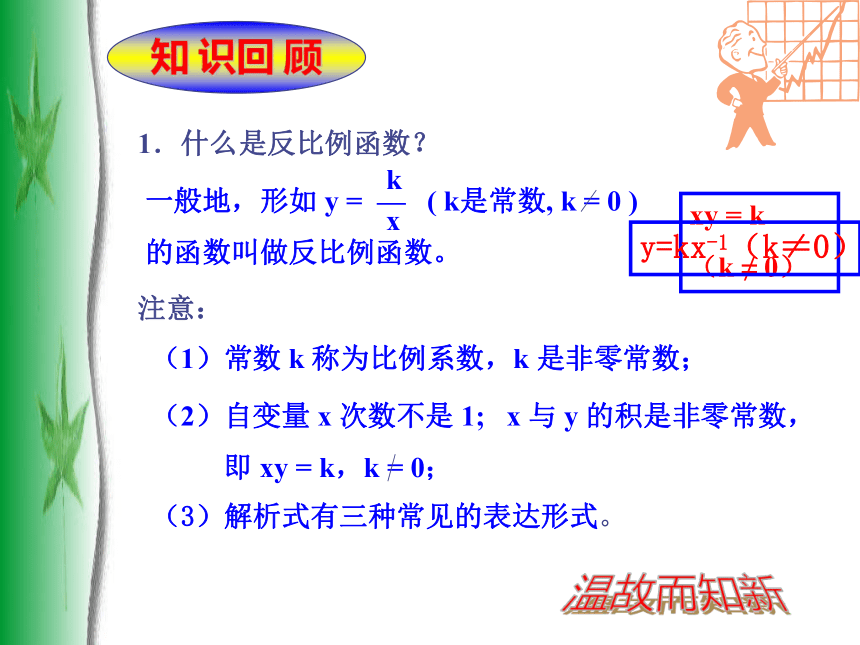
课件19张PPT。第五章 反比例函数复习课杨再成温故而知新1．什么是反比例函数？ 注意：（1）常数 k 称为比例系数，k 是非零常数；知 识回 顾（3）解析式有三种常见的表达形式。xy = k
（k ≠ 0）y=kx-1（k≠0）2.你能回顾总结一下反比例函数的图象性质特征吗? 与同伴进行交流. 图象是双曲线 当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内 当k>0时,在每一象限内,y随x的增大而减小

当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远不会与
坐标轴相交 双曲线既是轴对称图形又是中心对称图形.任意一组变量的乘积是一个定值,即xy=k形状
位置
增减性
变化趋势
对称性形 状位 置增减性变化趋势对称性思考;在叙述反比例函数性质时，要注意强调“在每一象限内”，谁能利用图象来说明为什么要加这个条件？位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
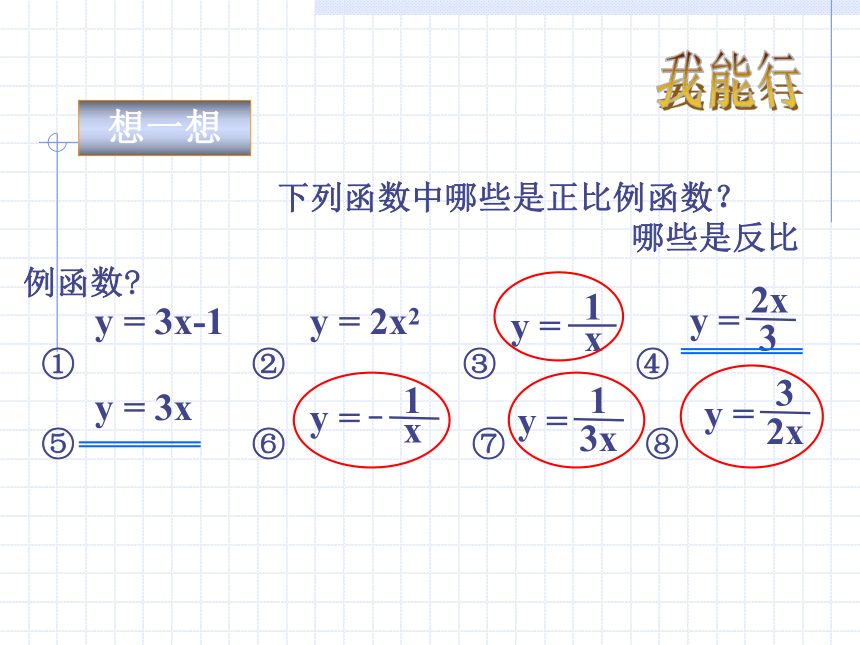
3、比较正、反比例函数的区别你知道？想一想 下列函数中哪些是正比例函数？
哪些是反比例函数?

① ② ③ ④

⑤ ⑥ ⑦ ⑧
y = 3x-1y = 2x2y = 3x我能行赋予反比例函数 一个现实生活中的实际意义。二、利用图象说明反比例函数和一次函数的关系写出这两个函数的相同点和不同点（至少两条）1、点（23，-3）在反比例函数 的图象
上，那么K= ，该反比例函数的图象位于第
象限。
-69二、四2、当M= 时，反比例函数 的图象在每个象限内Y随X的增大而增大。
-1问 题 探 讨y3< y1< y2问 题 探 讨 在平面直角坐标系内，从反比例函数y=k/x（k＞0））的图象上的一点分别作坐标轴的垂线段，与坐标轴围成的矩形的面积是12，请你求出该函数的解析式。探究无止境S1S2S1、S2有什么关系？为什么？反比例函数4、如图、一次函数的图象分别与x轴y轴交于A、B两点，与反比例函数图象交于C、D两点，如果A点坐标为（2，0），点C、D分别在第一、三象限内，且OA=OB=AC=BD，试求一次函数和反比例的表达式。实际应用 如图， 函数 和y=－kx+1(k≠0)在同一坐标系内的图
象大致是 （ ）BACDD先假设某个函数图象已经画好，
再确定另外一个是否符合条件.考察函数 的图象,
当x=-2时,y= ,
当x<-2时,y的取值范围是 ;
当y≥-1时,x的取值范围是 .-1y>-1x>0或x<-2谢谢各位老师光临指导!