人教版九年级上册数学22.3实际问题与二次函数——拱桥问题同步训练(含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数——拱桥问题同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 741.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 18:52:37 | ||
图片预览


文档简介
人教版九年级上册数学22.3实际问题与二次函数——拱桥问题同步训练
一、单选题
1.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为20m,此时水面到桥拱的距离是16m,则抛物线的函数关系式为( )
A. B. C. D.
2.如图,某拱形门建筑的形状时抛物线,拱形门地面上两点的跨度为192米,高度也为192米,若取拱形门地面上两点的连线作x轴,可用函数表示,则a的值为( )
A. B. C. D.
3.如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.4米 B.10米 C.4米 D.12米
4.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段AB上离中心M处5米的地方,桥的高度是( )
A.12米 B.13米 C.14米 D.15米
5.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
6.如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.
A.5 B.2 C.4 D.8
7.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度米,顶点距水面米(即米),小孔顶点距水面米(即米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度长为( )
A.米 B. C.米 D.米
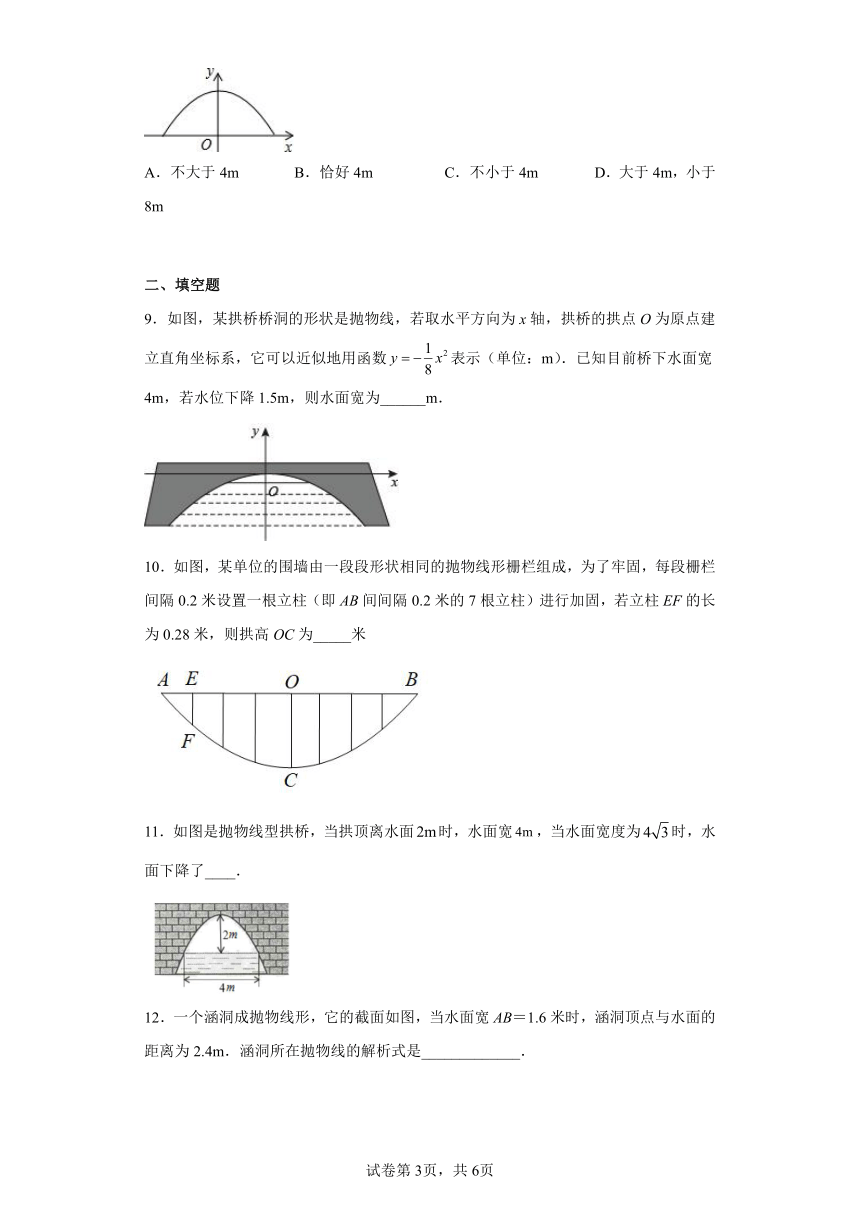
8.如图,隧道的截面是抛物线,可以用y= 表示,该隧道内设双行道,限高为3m,那么每条行道宽是( )
A.不大于4m B.恰好4m C.不小于4m D.大于4m,小于8m
二、填空题
9.如图,某拱桥桥洞的形状是抛物线,若取水平方向为x轴,拱桥的拱点O为原点建立直角坐标系,它可以近似地用函数表示(单位:m).已知目前桥下水面宽4m,若水位下降1.5m,则水面宽为______m.
10.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
11.如图是抛物线型拱桥,当拱顶离水面时,水面宽,当水面宽度为时,水面下降了____.
12.一个涵洞成抛物线形,它的截面如图,当水面宽AB=1.6米时,涵洞顶点与水面的距离为2.4m.涵洞所在抛物线的解析式是_____________.
13.某抛物线型拱桥的示意图如图,桥长 AB=48 米,拱桥最高处点 C 到水面 AB 的距离为 12 米,在该抛物线上的点 E、F 处要安装两盏警示灯(点 E、F 关于 y 轴对称),警示灯 F 距水面 AB 的高度是9米,则这两盏灯的水平距离EF是___米.
14.如图,一座悬索桥的桥面OA与主悬钢索MN之间用垂直钢索连接,主悬钢索是抛物线形状,两端到桥面的距离OM与AN相等.小强骑自行车从桥的一端0沿直线匀速穿过桥面到达另一端A,当他行驶18秒时和28秒时所在地方的主悬钢索的高度相同,那么他通过整个桥面OA共需_____________秒.
15.如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于,两点,拱桥最高点到的距离为,,,为拱桥底部的两点,且,若的长为,则点到直线的距离为______.
16.如图,平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣x2,桥下的水面宽AB为6m,当水位上涨2m时,水面宽CD为_____m(结果保留根号).
三、解答题
17.某公路有一个抛物线形状的隧道ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣x2+c且过顶点C(0,5).(长度单位:m)
(1)直接写出c= ;
(2)求该隧道截面的最大跨度(即AB的长度)是多少米?
(3)该隧道为双向车道,现有一辆运货卡车高4米、宽3米,问这辆卡车能否顺利通过隧道?请说明理由.
18.如图,隧道的截面由抛物线和矩形构成,矩形的长为,宽为,以所在的直线为轴,线段的中垂线为轴,建立平面直角坐标系.轴是抛物线的对称轴,最高点到地面距离为4米.
(1)求出抛物线的解析式.
(2)在距离地面米高处,隧道的宽度是多少?
(3)如果该隧道内设单行道(只能朝一个方向行驶),现有一辆货运卡车高3.6米,宽2.4米,这辆货运卡车能否通过该隧道?通过计算说明你的结论.
19.一座隧道的截面由抛物线和长方形构成,长方形的长OC为8m,宽OA为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系:
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,两辆同样的上述货车相对而行,是否可以同时在隧道内顺利通过,为什么?
20.如图所示.三孔桥横截面的三个孔是都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB为10m,顶点M距水面6m(即),小孔顶点N距水面4m(即),建立如图所示的平面直角坐标系.
(1)求出大孔抛物线的解析式;
(2)现有一艘船高度是4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,则这艘船在正常水位时能否安全通过拱桥大孔?
(3)当水位上涨到刚好淹没小孔时,求出此时大孔的水面宽度EF.
试卷第6页,共6页
试卷第5页,共6页
参考答案:
1.C
2.D
3.B
4.D
5.B
6.C
7.D
8.A
9.8
10.0.64
11.
12.
13.24
14.46
15.10m
16.2
17.(1)5;
(2)10米;
(3)能安全通过
18.(1)
(2)米
(3)能通过
19.(1)抛物线为:y=﹣+6;
(2)货车可以通过
(3)货车可以通过
20.(1)
(2)这艘船在正常水位时能安全通过拱桥大孔(3)
答案第2页,共2页
答案第1页,共1页
一、单选题
1.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为20m,此时水面到桥拱的距离是16m,则抛物线的函数关系式为( )
A. B. C. D.
2.如图,某拱形门建筑的形状时抛物线,拱形门地面上两点的跨度为192米,高度也为192米,若取拱形门地面上两点的连线作x轴,可用函数表示,则a的值为( )
A. B. C. D.
3.如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.4米 B.10米 C.4米 D.12米
4.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段AB上离中心M处5米的地方,桥的高度是( )
A.12米 B.13米 C.14米 D.15米
5.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
6.如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.
A.5 B.2 C.4 D.8
7.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度米,顶点距水面米(即米),小孔顶点距水面米(即米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度长为( )
A.米 B. C.米 D.米
8.如图,隧道的截面是抛物线,可以用y= 表示,该隧道内设双行道,限高为3m,那么每条行道宽是( )
A.不大于4m B.恰好4m C.不小于4m D.大于4m,小于8m
二、填空题
9.如图,某拱桥桥洞的形状是抛物线,若取水平方向为x轴,拱桥的拱点O为原点建立直角坐标系,它可以近似地用函数表示(单位:m).已知目前桥下水面宽4m,若水位下降1.5m,则水面宽为______m.
10.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为_____米
11.如图是抛物线型拱桥,当拱顶离水面时,水面宽,当水面宽度为时,水面下降了____.
12.一个涵洞成抛物线形,它的截面如图,当水面宽AB=1.6米时,涵洞顶点与水面的距离为2.4m.涵洞所在抛物线的解析式是_____________.
13.某抛物线型拱桥的示意图如图,桥长 AB=48 米,拱桥最高处点 C 到水面 AB 的距离为 12 米,在该抛物线上的点 E、F 处要安装两盏警示灯(点 E、F 关于 y 轴对称),警示灯 F 距水面 AB 的高度是9米,则这两盏灯的水平距离EF是___米.
14.如图,一座悬索桥的桥面OA与主悬钢索MN之间用垂直钢索连接,主悬钢索是抛物线形状,两端到桥面的距离OM与AN相等.小强骑自行车从桥的一端0沿直线匀速穿过桥面到达另一端A,当他行驶18秒时和28秒时所在地方的主悬钢索的高度相同,那么他通过整个桥面OA共需_____________秒.
15.如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于,两点,拱桥最高点到的距离为,,,为拱桥底部的两点,且,若的长为,则点到直线的距离为______.
16.如图,平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣x2,桥下的水面宽AB为6m,当水位上涨2m时,水面宽CD为_____m(结果保留根号).
三、解答题
17.某公路有一个抛物线形状的隧道ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣x2+c且过顶点C(0,5).(长度单位:m)
(1)直接写出c= ;
(2)求该隧道截面的最大跨度(即AB的长度)是多少米?
(3)该隧道为双向车道,现有一辆运货卡车高4米、宽3米,问这辆卡车能否顺利通过隧道?请说明理由.
18.如图,隧道的截面由抛物线和矩形构成,矩形的长为,宽为,以所在的直线为轴,线段的中垂线为轴,建立平面直角坐标系.轴是抛物线的对称轴,最高点到地面距离为4米.
(1)求出抛物线的解析式.
(2)在距离地面米高处,隧道的宽度是多少?
(3)如果该隧道内设单行道(只能朝一个方向行驶),现有一辆货运卡车高3.6米,宽2.4米,这辆货运卡车能否通过该隧道?通过计算说明你的结论.
19.一座隧道的截面由抛物线和长方形构成,长方形的长OC为8m,宽OA为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系:
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,两辆同样的上述货车相对而行,是否可以同时在隧道内顺利通过,为什么?
20.如图所示.三孔桥横截面的三个孔是都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB为10m,顶点M距水面6m(即),小孔顶点N距水面4m(即),建立如图所示的平面直角坐标系.
(1)求出大孔抛物线的解析式;
(2)现有一艘船高度是4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,则这艘船在正常水位时能否安全通过拱桥大孔?
(3)当水位上涨到刚好淹没小孔时,求出此时大孔的水面宽度EF.
试卷第6页,共6页
试卷第5页,共6页
参考答案:
1.C
2.D
3.B
4.D
5.B
6.C
7.D
8.A
9.8
10.0.64
11.
12.
13.24
14.46
15.10m
16.2
17.(1)5;
(2)10米;
(3)能安全通过
18.(1)
(2)米
(3)能通过
19.(1)抛物线为:y=﹣+6;
(2)货车可以通过
(3)货车可以通过
20.(1)
(2)这艘船在正常水位时能安全通过拱桥大孔(3)
答案第2页,共2页
答案第1页,共1页
同课章节目录
