人教版九年级上册数学22.3实际问题与二次函数——图形问题同步训练(含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数——图形问题同步训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 376.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 18:54:48 | ||
图片预览


文档简介
人教版九年级上册数学22.3实际问题与二次函数——图形问题同步训练
一、单选题
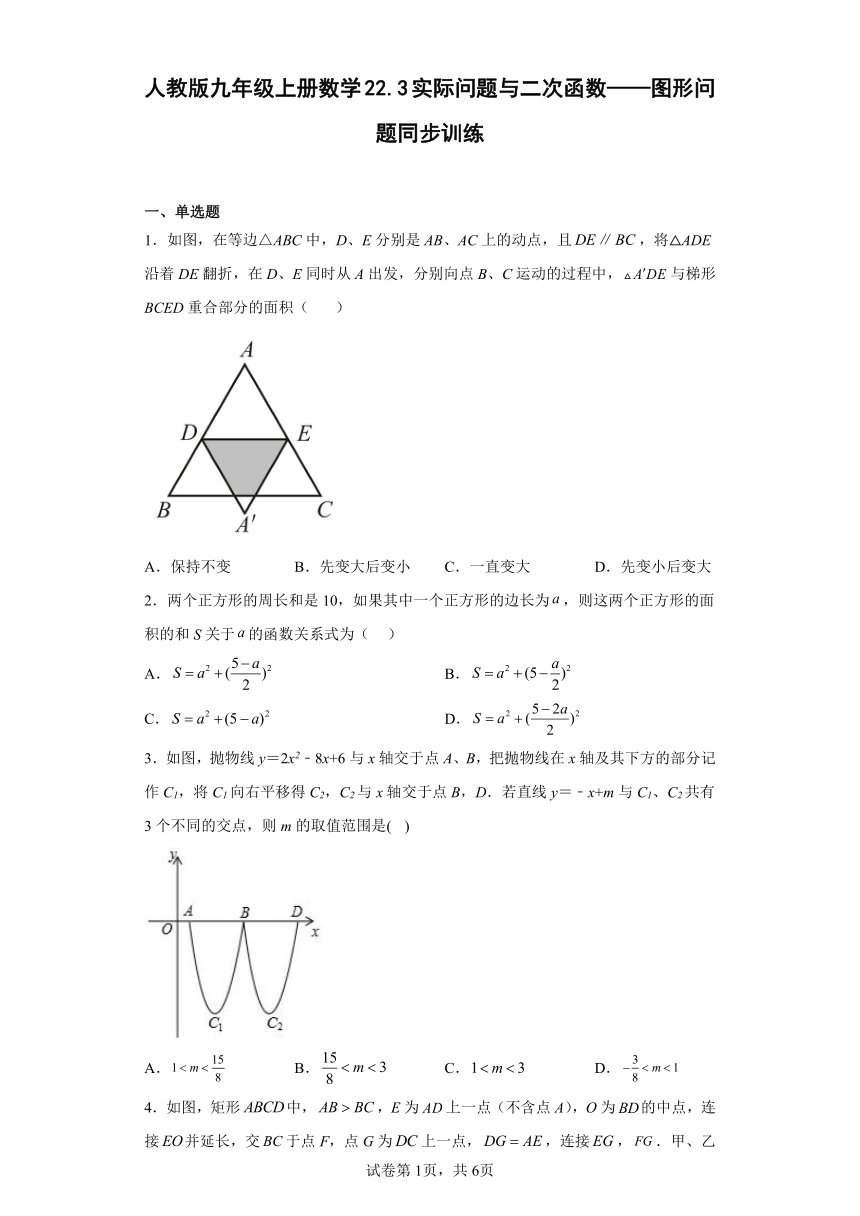
1.如图,在等边△ABC中,D、E分别是AB、AC上的动点,且,将△ADE沿着DE翻折,在D、E同时从A出发,分别向点B、C运动的过程中,与梯形BCED重合部分的面积( )
A.保持不变 B.先变大后变小 C.一直变大 D.先变小后变大
2.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
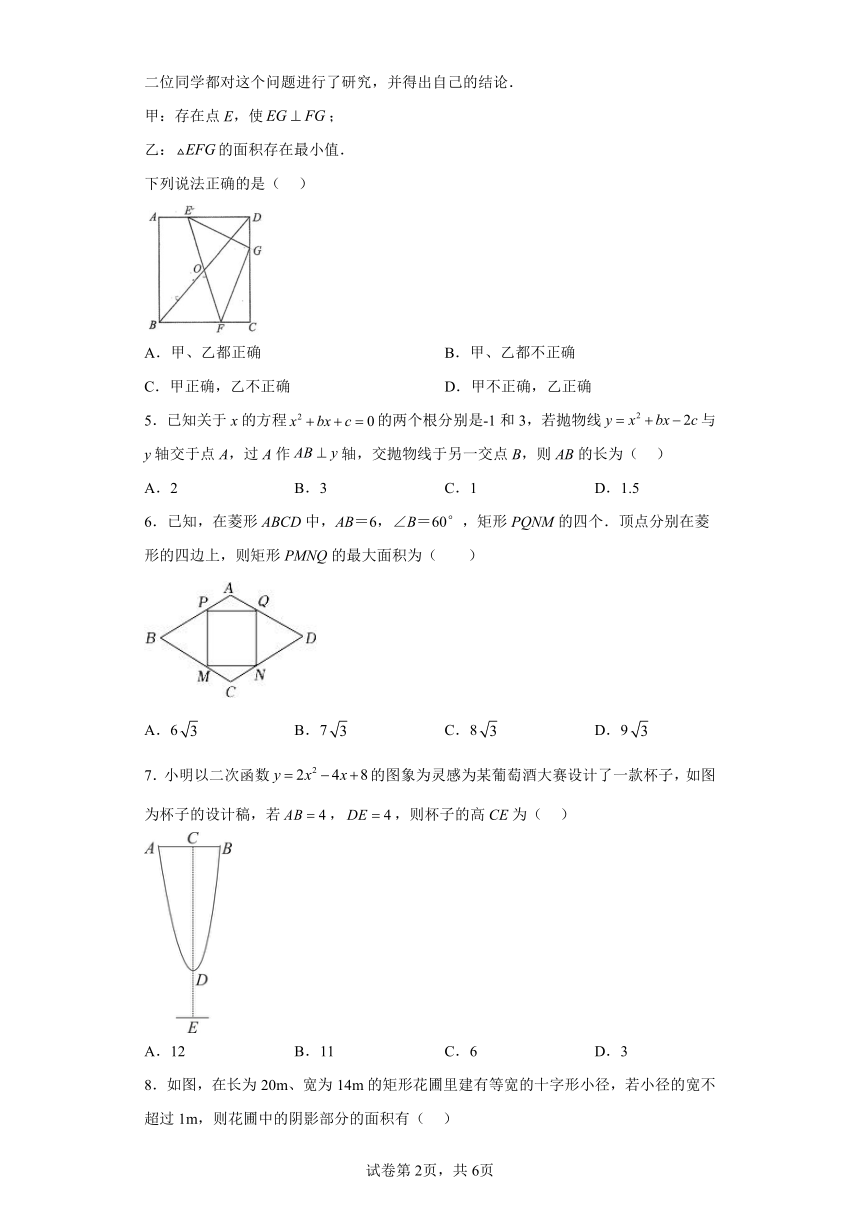
3.如图,抛物线y=2x2﹣8x+6与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=﹣x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
4.如图,矩形中,,E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点,,连接,.甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.
甲:存在点E,使;
乙:的面积存在最小值.
下列说法正确的是( )
A.甲、乙都正确 B.甲、乙都不正确
C.甲正确,乙不正确 D.甲不正确,乙正确
5.已知关于x的方程的两个根分别是-1和3,若抛物线与y轴交于点A,过A作轴,交抛物线于另一交点B,则AB的长为( )
A.2 B.3 C.1 D.1.5
6.已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
7.小明以二次函数的图象为灵感为某葡萄酒大赛设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高CE为( )
A.12 B.11 C.6 D.3
8.如图,在长为20m、宽为14m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1m,则花圃中的阴影部分的面积有( )
A.最小值247 B.最小值266 C.最大值247 D.最大值266
二、填空题
9.如图用一段长为16m的篱笆围成一个一边靠墙的矩形围栏(墙长9m),则这个围栏的最大面积为________ .
10.某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙长20米),另外三边用篱笆围成如图所示,所用的篱笆长为32米.请问当垂直于墙的一边的长为____米时,花圃的面积有最大值,最大值是____.
11.如图,在一块等腰直角三角形ABC的铁皮上截取一块矩形铁皮,要求截得的矩形的边EF在的边BC上,顶点D、G分别在边AB、AC上.已知厘米,设DG的长为x厘米,矩形DEFG的面积为y平方厘米,那么y关于x的函数解析式为__________.(不要求写出定义域)
12.如图利用135°的墙角修建一个梯形的储料场,并使∠C=90°.如果新建的墙BCD总长24m,那么BC=________储料场的面积最大.
13.如图,抛物线的顶点为,与轴交于点,轴,与抛物线交于点,轴,与射线交于点,,则_______.
14.矩形ABCD中,点P从点A出发,沿AB边以每秒1个单位的速度向B点运动,至B点停止;同时点Q也从A点出发,以同样的速度沿A-D-C-B的路径运动,至B点停止,在此过程中△APQ的面积y与运动时间t的函数关系图象如图所示,则m的值为________
15.一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是____cm.
16.如图,一个长为5,宽为3的矩形被平行于边的两条直线所割,其中矩形的左上角是一个边长为的正方形,则阴影部分面积的最小值为________.
三、解答题
17.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)设BC长为x米,矩形ABCD的面积为y平方米,求y与x的函数关系式;
(2)若a=40,求矩形菜园ABCD面积的最大值.
18.南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“L”字形的墙面(粗线ABC表示墙面,已知AB⊥BC,AB=3米,BC=1米)和总长为11米的篱笆围建一个“日”字形的小型农场DBEF(细线表示篱笆,小型农场中间GH也是用篱笆隔开),点D可能在线段AB上(如图1),也可能在线段BA的延长线上(如图2),点E在线段BC的延长线上.
(1)当点D在线段AB上时,
①设DF的长为x米,请用含x的代数式表示EF的长;
②若要求所围成的小型农场DBEF的面积为9平方米,求DF的长;
(2)DF的长为多少米时,小型农场DBEF的面积最大?最大面积为多少平方米?
19.如图,用一段长为30 米的篱笆围成一个一边靠墙的矩形苗圃园,墙长为18 米,设这个苗圃园垂直于墙的一边AB的长为x 米.
(1)若苗圃园的面积为72 平方米,求AB的长.
(2)当x为何值时,苗圃的面积最大?最大值为多少平方米?
20.如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
(1)探究1:如果木板边长为2米,FC=1米,则一块木板用墙纸的费用需_____元;
(2)探究2:如果木板边长为1米,当FC的长为多少时,一块木板需用墙纸的费用最省?最省是多少元?
(3)探究3:设木板的边长为a(a为整数),当正方形EFCG的边长为多少时,墙纸费用最省?
试卷第2页,共6页
试卷第1页,共6页
参考答案:
1.B
2.D
3.B
4.D
5.A
6.D
7.A
8.A
9.32
10. 8 128平方米##128m2
11.
12.16
13.
14.24
15.2
16.7
17.(1)
(2)1200平方米
18.(1)①(12﹣3x)米;②3米
(2)饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米
19.(1)AB的长为12米
(2)当时,苗圃园的面积有最大值,最大值是平方米
20.(1)220;
(2)当FC的长为m时,一块木板需用墙纸的费用最省,最省是55元;
(3)当正方形EFCG的边长为时,墙纸费用最省.
答案第2页,共2页
一、单选题
1.如图,在等边△ABC中,D、E分别是AB、AC上的动点,且,将△ADE沿着DE翻折,在D、E同时从A出发,分别向点B、C运动的过程中,与梯形BCED重合部分的面积( )
A.保持不变 B.先变大后变小 C.一直变大 D.先变小后变大
2.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
3.如图,抛物线y=2x2﹣8x+6与x轴交于点A、B,把抛物线在x轴及其下方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=﹣x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A. B. C. D.
4.如图,矩形中,,E为上一点(不含点A),O为的中点,连接并延长,交于点F,点G为上一点,,连接,.甲、乙二位同学都对这个问题进行了研究,并得出自己的结论.
甲:存在点E,使;
乙:的面积存在最小值.
下列说法正确的是( )
A.甲、乙都正确 B.甲、乙都不正确
C.甲正确,乙不正确 D.甲不正确,乙正确
5.已知关于x的方程的两个根分别是-1和3,若抛物线与y轴交于点A,过A作轴,交抛物线于另一交点B,则AB的长为( )
A.2 B.3 C.1 D.1.5
6.已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A.6 B.7 C.8 D.9
7.小明以二次函数的图象为灵感为某葡萄酒大赛设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高CE为( )
A.12 B.11 C.6 D.3
8.如图,在长为20m、宽为14m的矩形花圃里建有等宽的十字形小径,若小径的宽不超过1m,则花圃中的阴影部分的面积有( )
A.最小值247 B.最小值266 C.最大值247 D.最大值266
二、填空题
9.如图用一段长为16m的篱笆围成一个一边靠墙的矩形围栏(墙长9m),则这个围栏的最大面积为________ .
10.某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙长20米),另外三边用篱笆围成如图所示,所用的篱笆长为32米.请问当垂直于墙的一边的长为____米时,花圃的面积有最大值,最大值是____.
11.如图,在一块等腰直角三角形ABC的铁皮上截取一块矩形铁皮,要求截得的矩形的边EF在的边BC上,顶点D、G分别在边AB、AC上.已知厘米,设DG的长为x厘米,矩形DEFG的面积为y平方厘米,那么y关于x的函数解析式为__________.(不要求写出定义域)
12.如图利用135°的墙角修建一个梯形的储料场,并使∠C=90°.如果新建的墙BCD总长24m,那么BC=________储料场的面积最大.
13.如图,抛物线的顶点为,与轴交于点,轴,与抛物线交于点,轴,与射线交于点,,则_______.
14.矩形ABCD中,点P从点A出发,沿AB边以每秒1个单位的速度向B点运动,至B点停止;同时点Q也从A点出发,以同样的速度沿A-D-C-B的路径运动,至B点停止,在此过程中△APQ的面积y与运动时间t的函数关系图象如图所示,则m的值为________
15.一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是____cm.
16.如图,一个长为5,宽为3的矩形被平行于边的两条直线所割,其中矩形的左上角是一个边长为的正方形,则阴影部分面积的最小值为________.
三、解答题
17.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)设BC长为x米,矩形ABCD的面积为y平方米,求y与x的函数关系式;
(2)若a=40,求矩形菜园ABCD面积的最大值.
18.南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“L”字形的墙面(粗线ABC表示墙面,已知AB⊥BC,AB=3米,BC=1米)和总长为11米的篱笆围建一个“日”字形的小型农场DBEF(细线表示篱笆,小型农场中间GH也是用篱笆隔开),点D可能在线段AB上(如图1),也可能在线段BA的延长线上(如图2),点E在线段BC的延长线上.
(1)当点D在线段AB上时,
①设DF的长为x米,请用含x的代数式表示EF的长;
②若要求所围成的小型农场DBEF的面积为9平方米,求DF的长;
(2)DF的长为多少米时,小型农场DBEF的面积最大?最大面积为多少平方米?
19.如图,用一段长为30 米的篱笆围成一个一边靠墙的矩形苗圃园,墙长为18 米,设这个苗圃园垂直于墙的一边AB的长为x 米.
(1)若苗圃园的面积为72 平方米,求AB的长.
(2)当x为何值时,苗圃的面积最大?最大值为多少平方米?
20.如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元.
(1)探究1:如果木板边长为2米,FC=1米,则一块木板用墙纸的费用需_____元;
(2)探究2:如果木板边长为1米,当FC的长为多少时,一块木板需用墙纸的费用最省?最省是多少元?
(3)探究3:设木板的边长为a(a为整数),当正方形EFCG的边长为多少时,墙纸费用最省?
试卷第2页,共6页
试卷第1页,共6页
参考答案:
1.B
2.D
3.B
4.D
5.A
6.D
7.A
8.A
9.32
10. 8 128平方米##128m2
11.
12.16
13.
14.24
15.2
16.7
17.(1)
(2)1200平方米
18.(1)①(12﹣3x)米;②3米
(2)饲养场的宽DF为米时,饲养场DBEF的面积最大,最大面积为平方米
19.(1)AB的长为12米
(2)当时,苗圃园的面积有最大值,最大值是平方米
20.(1)220;
(2)当FC的长为m时,一块木板需用墙纸的费用最省,最省是55元;
(3)当正方形EFCG的边长为时,墙纸费用最省.
答案第2页,共2页
同课章节目录
