人教版九年级上册数学22.3实际问题与二次函数——喷水问题同步训练(含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数——喷水问题同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 337.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 19:19:48 | ||
图片预览


文档简介
人教版九年级上册数学22.3实际问题与二次函数——喷水问题同步训练
一、单选题
1.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
2.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子恰为水面中心,安置在柱子顶端处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,在过的任一平面上,建立平面直角 坐标系(如图),水流喷出的高度与水平距离之间的关系式是 ,则下列结论错误的是( )
A.柱子的高度为
B.喷出的水流距柱子处达到最大高度
C.喷出的水流距水平面的最大高度是
D.水池的半径至少要才能使喷出的水流不至于落在池外
3.某公园有一个圆形喷水池,喷出的水流呈抛物线状,一条水流的高度与水流时间之间的解析式为,那么水流从抛出至落到地面所需要的时间是( )
A. B. C. D.
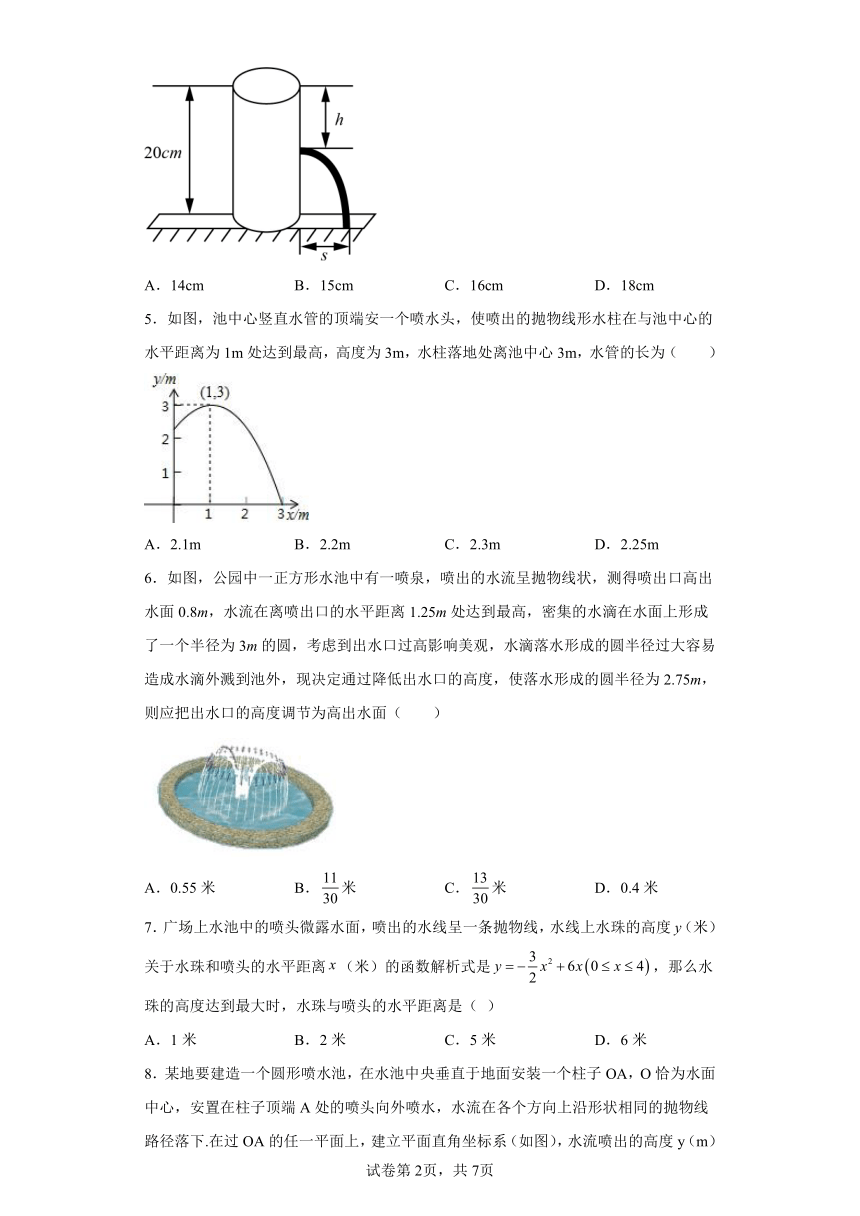
4.如图,始终盛满水的圆柱体水桶水面离地面的高度为20cm,如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系式为.如果想通过垫高水桶,使射出水的最大射程增加10cm,则小孔离水面的距离是( )
A.14cm B.15cm C.16cm D.18cm
5.如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
A.2.1m B.2.2m C.2.3m D.2.25m
6.如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米 B.米 C.米 D.0.4米
7.广场上水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离(米)的函数解析式是,那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米 B.2米 C.5米 D.6米
8.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+,则下列结论:
(1)柱子OA的高度为m;
(2)喷出的水流距柱子1m处达到最大高度;
(3)喷出的水流距水平面的最大高度是2.5m;
(4)水池的半径至少要2.5m才能使喷出的水流不至于落在池外.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,某广场有一喷水池,水从地面喷出,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣2x2+8x(单位:米)的一部分,则水喷出的最大高度是________米.
10.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
11.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是__________米.
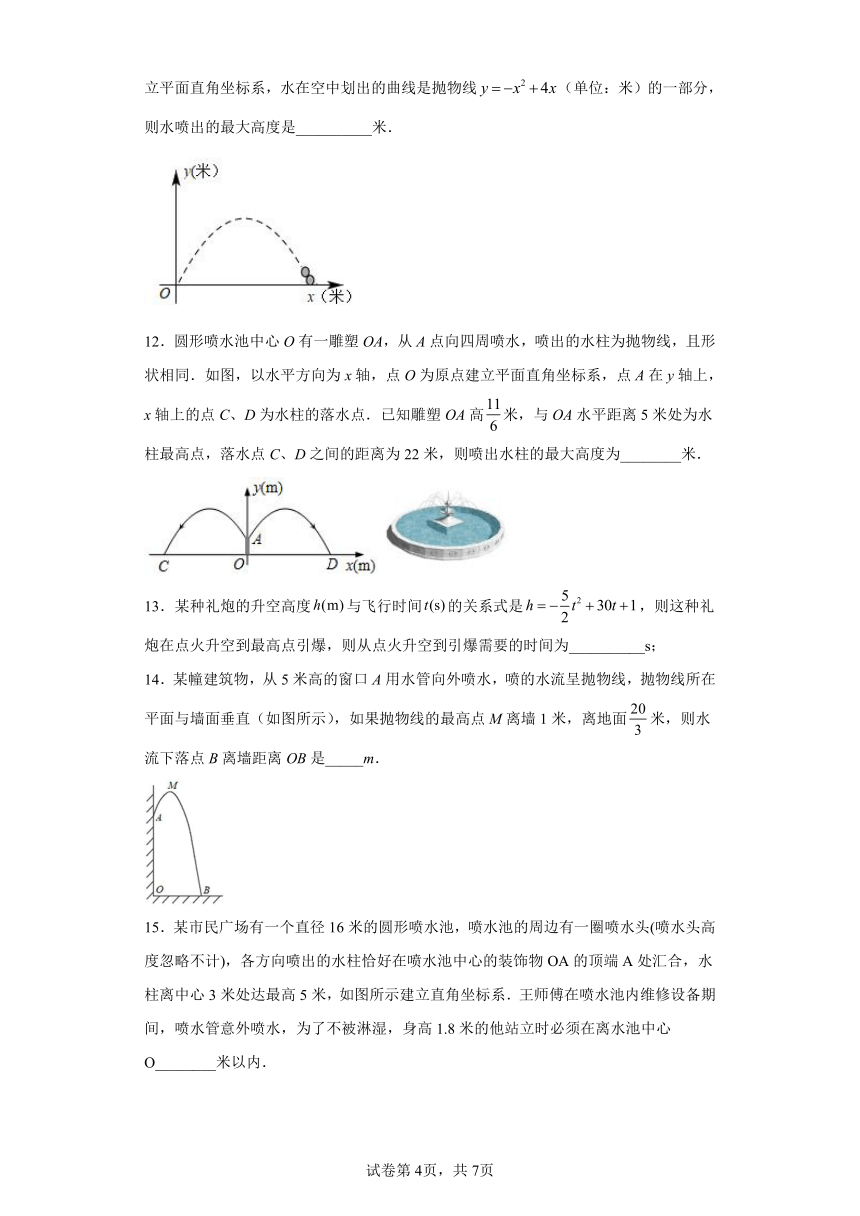
12.圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为________米.
13.某种礼炮的升空高度与飞行时间的关系式是,则这种礼炮在点火升空到最高点引爆,则从点火升空到引爆需要的时间为__________s;
14.某幢建筑物,从5米高的窗口A用水管向外喷水,喷的水流呈抛物线,抛物线所在平面与墙面垂直(如图所示),如果抛物线的最高点M离墙1米,离地面米,则水流下落点B离墙距离OB是_____m.
15.某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O________米以内.
16.如图,公园里喷水池中的水柱的形状可以看成是抛物线,小明想知道水柱的最大高度,于是画出示意图,并测出了一些数据:水柱上的点C,D到地面的距离都是1.6米,即米,米,米,则水柱的最大高度是______米.
三、解答题
17.某地要建造一个圆形喷水池,在水池中央竖直安装一根水管OA,O为水管与地面交点,在水管顶端A处安装一个喷水头,使喷出的水流在各个方向上沿形状相同的抛物线路径落下,在过OA的任一平面上,以O为原点,以原点与水流落地点所在直线为x轴,以OA所在直线为y轴,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是.
(1)求水管OA的高度;
(2)求喷出的水流距地面的最大高度;
(3)若要使喷出的水流不落在池外,试求水池的半径至少要多少米?
18.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的,如图所示,水柱的最高点为M,,,水嘴高,以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,求出图中抛物线的表达式.
19.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线,图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌底部的距离)是1米,当喷射出的水流距离喷灌架水平距离为20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.
(1)求水流运行轨迹满足的函数关系式;
(2)若将喷灌向后移动5米,通过计算说明是否可避开对这棵石榴树的喷灌?
(3)设喷射水流与坡面OA之间的铅直高度为h,求h的表达式,并求出x为何值时,h有最大值,h最大值是多少?
20.如图是某公园一喷水池(示意图),在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25.
(1)求喷出的水流离地面的最大高度;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
试卷第6页,共7页
试卷第7页,共7页
参考答案:
1.D
2.C
3.B
4.B
5.D
6.B
7.B
8.C
9.8
10.8
11.4
12.6
13.6
14.
15.7
16.
17.(1)水管OA的高度为m
(2)喷出的水流距地面的最大高度为2m
(3)水池的半径至少要3米
18.
19.(1)
(2)可避开对这棵石榴树的喷灌
(3)当x=18时,h有最大值,最大值为9.1m
20.(1)喷出的水流离地面的最大高度为2.25m;(2)水池半径至少为2.5m时,才能使喷出的水流不落在水池.
答案第1页,共2页
答案第1页,共1页
一、单选题
1.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
2.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子恰为水面中心,安置在柱子顶端处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,在过的任一平面上,建立平面直角 坐标系(如图),水流喷出的高度与水平距离之间的关系式是 ,则下列结论错误的是( )
A.柱子的高度为
B.喷出的水流距柱子处达到最大高度
C.喷出的水流距水平面的最大高度是
D.水池的半径至少要才能使喷出的水流不至于落在池外
3.某公园有一个圆形喷水池,喷出的水流呈抛物线状,一条水流的高度与水流时间之间的解析式为,那么水流从抛出至落到地面所需要的时间是( )
A. B. C. D.
4.如图,始终盛满水的圆柱体水桶水面离地面的高度为20cm,如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系式为.如果想通过垫高水桶,使射出水的最大射程增加10cm,则小孔离水面的距离是( )
A.14cm B.15cm C.16cm D.18cm
5.如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
A.2.1m B.2.2m C.2.3m D.2.25m
6.如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米 B.米 C.米 D.0.4米
7.广场上水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离(米)的函数解析式是,那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米 B.2米 C.5米 D.6米
8.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+,则下列结论:
(1)柱子OA的高度为m;
(2)喷出的水流距柱子1m处达到最大高度;
(3)喷出的水流距水平面的最大高度是2.5m;
(4)水池的半径至少要2.5m才能使喷出的水流不至于落在池外.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,某广场有一喷水池,水从地面喷出,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣2x2+8x(单位:米)的一部分,则水喷出的最大高度是________米.
10.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
11.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是__________米.
12.圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距离为22米,则喷出水柱的最大高度为________米.
13.某种礼炮的升空高度与飞行时间的关系式是,则这种礼炮在点火升空到最高点引爆,则从点火升空到引爆需要的时间为__________s;
14.某幢建筑物,从5米高的窗口A用水管向外喷水,喷的水流呈抛物线,抛物线所在平面与墙面垂直(如图所示),如果抛物线的最高点M离墙1米,离地面米,则水流下落点B离墙距离OB是_____m.
15.某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O________米以内.
16.如图,公园里喷水池中的水柱的形状可以看成是抛物线,小明想知道水柱的最大高度,于是画出示意图,并测出了一些数据:水柱上的点C,D到地面的距离都是1.6米,即米,米,米,则水柱的最大高度是______米.
三、解答题
17.某地要建造一个圆形喷水池,在水池中央竖直安装一根水管OA,O为水管与地面交点,在水管顶端A处安装一个喷水头,使喷出的水流在各个方向上沿形状相同的抛物线路径落下,在过OA的任一平面上,以O为原点,以原点与水流落地点所在直线为x轴,以OA所在直线为y轴,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是.
(1)求水管OA的高度;
(2)求喷出的水流距地面的最大高度;
(3)若要使喷出的水流不落在池外,试求水池的半径至少要多少米?
18.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的,如图所示,水柱的最高点为M,,,水嘴高,以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,求出图中抛物线的表达式.
19.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线,图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌底部的距离)是1米,当喷射出的水流距离喷灌架水平距离为20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.
(1)求水流运行轨迹满足的函数关系式;
(2)若将喷灌向后移动5米,通过计算说明是否可避开对这棵石榴树的喷灌?
(3)设喷射水流与坡面OA之间的铅直高度为h,求h的表达式,并求出x为何值时,h有最大值,h最大值是多少?
20.如图是某公园一喷水池(示意图),在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25.
(1)求喷出的水流离地面的最大高度;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
试卷第6页,共7页
试卷第7页,共7页
参考答案:
1.D
2.C
3.B
4.B
5.D
6.B
7.B
8.C
9.8
10.8
11.4
12.6
13.6
14.
15.7
16.
17.(1)水管OA的高度为m
(2)喷出的水流距地面的最大高度为2m
(3)水池的半径至少要3米
18.
19.(1)
(2)可避开对这棵石榴树的喷灌
(3)当x=18时,h有最大值,最大值为9.1m
20.(1)喷出的水流离地面的最大高度为2.25m;(2)水池半径至少为2.5m时,才能使喷出的水流不落在水池.
答案第1页,共2页
答案第1页,共1页
同课章节目录
