人教版七上1.5.1有理数的乘方(第1课时) 课件(共29张PPT)
文档属性
| 名称 | 人教版七上1.5.1有理数的乘方(第1课时) 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 08:41:01 | ||
图片预览








文档简介
(共29张PPT)
1.5.1有理数的乘方
(第1课时)
人教版七年级上册
教学目标
教学重点:
有理数乘方的定义及法则运用.
教学难点:
进行有理数的乘方运算及初步使用计算器计算有理数的乘方.
1.正确理解乘方、幂、指数、底数等概念.
2.会进行有理数乘方的运算,及初步使用计算器计算有理数的乘方.
3.培养学生观察比较、分析、归纳概括的能力,渗透转化思想.
新知导入
古希腊数学家阿基米德与国王下棋,国王输了,问阿基米德要什么奖赏.阿基米德对国王说:“我只要在棋盘上第1个格放1粒米,在第2个格放2粒米,在第3个格放4粒米,在第4个格放8粒米,然后12粒米,32粒米┉┉”国王觉得很容易就可以满足他的要求,于是就同意了.但很快国王就发现,即使将国库所有的粮食都给他也不够.你们知道这是为什么吗?你能用数学知识来说明?
棋盘上的学问
新知讲解
(1)边长为2的正方形的面积记为:
(2)棱长为2的正方体的体积可记为:
2×2=4
2×2×2=8
2
2
新知讲解
2×2=4
2×2×2=8
观察下面两个式子,你们有什么发现呢?
2×2,2×2×2都是相同因数的乘法.
我们发现:
2×2表示2个2相乘,
记作为:
读作为:“2的平方”.
2×2×2表示3个2相乘,
记作为:
读作为:“2的立方”
或2的三次方”.
新知讲解
× × ×
记作,
记作,
仿照上面的式子,下面式子如何记作成什么,读作成什么呢?
读作
读作:
“ 的五次方”.
× × × ×
“ 的四次方”.
表示4个 相乘.
表示5个相乘.
新知讲解
个
2×2×… ×2×2
n个
记作,
读作:
“ 的n次方”.
表示个 相乘.
表示个相乘.
记作,
读作:
“ 的次方”.
新知讲解
× × ×
× × × ×
2×2×… ×2×2
个
个
观察下面四个式子,它们有什么共同特征呢?
它们都是乘法运算,它们各个乘数都相等.
新知讲解
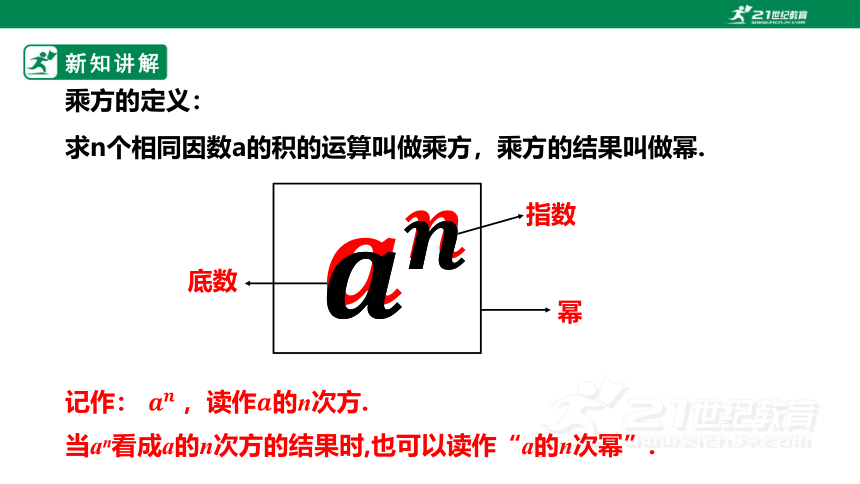
记作: ,读作的n次方.
求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂.
乘方的定义:
底数
指数
幂
当an看成a的n次方的结果时,也可以读作“a的n次幂”.
新知讲解
如:在 94中,9叫做 ,4叫做 ,读作“ ”,也可以读作“ ”.
底数
指数
9的4次方
9的4次幂
一个数可以看作这个数本身的一次方.例如,5就是.指数1通常省略不写.
新知讲解
注意∶
an
底数
指数
幂
1.指数n取正整数.
2.底数a可以代表所有数,可以是正数,负数,零.
3.一个数可以看作这个数本身的一次方,指数1通常省略不写.
4.负数的乘方,在书写时,要把整个负数用小括号括起来.
5.分数的乘方,在书写时,要把整个分数用小括号括起来.
练一练
棋盘上的米粒
第1个格:1
第2个格:2
第3个格:4=2╳2
第4个格: .
第5个格: .
第6个格: .
┉ ┉
第20个格,第64个格,如何表示?
8=2╳2 ╳2
16=2╳2 ╳2 ╳2 ╳2
32=2╳2 ╳2 ╳2 ╳2 ╳2
=22
=23
=24
=25
=219
=263
练一练
1. 的底数是 ,指数是 , 表示的意义是 .
4. 9的底数是 ,指数是 .
3. 的底数是 ,指数是 , 表示的意义是 .
2. 的底数是 ,指数是 , 表示的意义是 .
5
2
10
2个 5相乘
5个10相乘
5
7
9
1
7个 相乘
新知讲解
幂
底数
指数
表示意义
读法
结果
2
2
4
4
4个 2相乘
4的2的积的相反数
2的4次方
2的4次方的相反数
16
16
新知讲解
例1 计算:
=( 4)╳( 4)╳( 4)
= 64
=( 2)╳( 2)╳( 2) ╳( 2)
=16
=()╳()╳()=
新知讲解
计算:
.
.
.
.
.
.
.
.
.
.
观察上面的结果,你发现幂的运算有什么规律?
9
16
125
81
新知讲解
当指数是 时,负数的幂是 ;
奇数
负数
正数的任何次幂都是 ;0的任何正整数次幂都是 .
正数
0
当指数是 时,负数的幂是 ;
偶数
正数
1的奇次幂结果是 , 1的偶次幂结果是 .
1
1
归纳:
新知讲解
例2.用计算器计算( 8)5和( 3)6.
显示:(─ 8)∧5
─32768
显示:(─ 3)∧6
729.
所以( 8)5= 32768,( 3)6=729.
解:用带符号键 的计算器.
(─ 8)∧5
─32768
(─ 3)∧6
729
练一练
用计算器计算( 11)6和167.
显示:(─ 11)∧6
1771561
显示:16∧7
268435456
所以( 11)6=1771561,167=268435456
解:用带符号键 的计算器.
(─ 11)∧6
1771561
16∧7
268435456
课堂练习
1.下列说法正确的是( ).
读作 3的4次幂
B.的底数是 3,指数是4
C. 表示4个3相乘的积的相反数
D. 表示4个 3相乘的积
2.下列说法正确的是( ).
A. 25表示2×5
C. 32与( 3)2互为相反数
B. 25中2是底数,5是幂
D. a5=( a)5
C
C
课堂练习
3. 计算: 14的结果是( )
A. 1 B. 1 C. 4 D.4
4.规定一种新运算: ,如 .则 的值是( ).
A. B. C. 6 D.
B
C
课堂练习
5.下列各式中结果是负数的为( )
A. ( 5) B. ( 5)2
C. 52 D. | 5|
6. 在 ( 3), | 6|, ( 2)2 , 5这四个数中,比 4小的数是( )
A. ( 3) B. | 6|
C. ( 2)2 D. 5
C
B
课堂练习
7.你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示.这样捏合到第7次后可拉出 根细面条.
64
课堂练习
8.计算:
=( 5)╳( 5)╳( 5)
= 125
=( 3)╳( 3)╳( 3) ╳( 3)
=81
=()╳()╳()=
课堂练习
9. 规定两数a,b之间的一种运算,记作(a, b):如果那么(a,b)=c.例如:因为所以(2,8)=3
(1)根据上述规定,填空:(3,9)=________, (4,64)=________.
(2)(4,a)=2, (b,8)=3,= .
2
3
4
课堂总结
1.乘方的定义及表示的意义.
2.乘方的读法:① 读作的次方(看作运算)
② 读作的次幂(看作结果)
二.有理数乘方的运算:
当指数是 时,负数的幂是 ;
奇数
负数
正数的任何次幂都是 ;0的任何正整数次幂都是 .
正数
0
当指数是 时,负数的幂是 ;
偶数
正数
一.乘方
作业布置
习题1.5
第47第1题和第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5.1有理数的乘方
(第1课时)
人教版七年级上册
教学目标
教学重点:
有理数乘方的定义及法则运用.
教学难点:
进行有理数的乘方运算及初步使用计算器计算有理数的乘方.
1.正确理解乘方、幂、指数、底数等概念.
2.会进行有理数乘方的运算,及初步使用计算器计算有理数的乘方.
3.培养学生观察比较、分析、归纳概括的能力,渗透转化思想.
新知导入
古希腊数学家阿基米德与国王下棋,国王输了,问阿基米德要什么奖赏.阿基米德对国王说:“我只要在棋盘上第1个格放1粒米,在第2个格放2粒米,在第3个格放4粒米,在第4个格放8粒米,然后12粒米,32粒米┉┉”国王觉得很容易就可以满足他的要求,于是就同意了.但很快国王就发现,即使将国库所有的粮食都给他也不够.你们知道这是为什么吗?你能用数学知识来说明?
棋盘上的学问
新知讲解
(1)边长为2的正方形的面积记为:
(2)棱长为2的正方体的体积可记为:
2×2=4
2×2×2=8
2
2
新知讲解
2×2=4
2×2×2=8
观察下面两个式子,你们有什么发现呢?
2×2,2×2×2都是相同因数的乘法.
我们发现:
2×2表示2个2相乘,
记作为:
读作为:“2的平方”.
2×2×2表示3个2相乘,
记作为:
读作为:“2的立方”
或2的三次方”.
新知讲解
× × ×
记作,
记作,
仿照上面的式子,下面式子如何记作成什么,读作成什么呢?
读作
读作:
“ 的五次方”.
× × × ×
“ 的四次方”.
表示4个 相乘.
表示5个相乘.
新知讲解
个
2×2×… ×2×2
n个
记作,
读作:
“ 的n次方”.
表示个 相乘.
表示个相乘.
记作,
读作:
“ 的次方”.
新知讲解
× × ×
× × × ×
2×2×… ×2×2
个
个
观察下面四个式子,它们有什么共同特征呢?
它们都是乘法运算,它们各个乘数都相等.
新知讲解
记作: ,读作的n次方.
求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂.
乘方的定义:
底数
指数
幂
当an看成a的n次方的结果时,也可以读作“a的n次幂”.
新知讲解
如:在 94中,9叫做 ,4叫做 ,读作“ ”,也可以读作“ ”.
底数
指数
9的4次方
9的4次幂
一个数可以看作这个数本身的一次方.例如,5就是.指数1通常省略不写.
新知讲解
注意∶
an
底数
指数
幂
1.指数n取正整数.
2.底数a可以代表所有数,可以是正数,负数,零.
3.一个数可以看作这个数本身的一次方,指数1通常省略不写.
4.负数的乘方,在书写时,要把整个负数用小括号括起来.
5.分数的乘方,在书写时,要把整个分数用小括号括起来.
练一练
棋盘上的米粒
第1个格:1
第2个格:2
第3个格:4=2╳2
第4个格: .
第5个格: .
第6个格: .
┉ ┉
第20个格,第64个格,如何表示?
8=2╳2 ╳2
16=2╳2 ╳2 ╳2 ╳2
32=2╳2 ╳2 ╳2 ╳2 ╳2
=22
=23
=24
=25
=219
=263
练一练
1. 的底数是 ,指数是 , 表示的意义是 .
4. 9的底数是 ,指数是 .
3. 的底数是 ,指数是 , 表示的意义是 .
2. 的底数是 ,指数是 , 表示的意义是 .
5
2
10
2个 5相乘
5个10相乘
5
7
9
1
7个 相乘
新知讲解
幂
底数
指数
表示意义
读法
结果
2
2
4
4
4个 2相乘
4的2的积的相反数
2的4次方
2的4次方的相反数
16
16
新知讲解
例1 计算:
=( 4)╳( 4)╳( 4)
= 64
=( 2)╳( 2)╳( 2) ╳( 2)
=16
=()╳()╳()=
新知讲解
计算:
.
.
.
.
.
.
.
.
.
.
观察上面的结果,你发现幂的运算有什么规律?
9
16
125
81
新知讲解
当指数是 时,负数的幂是 ;
奇数
负数
正数的任何次幂都是 ;0的任何正整数次幂都是 .
正数
0
当指数是 时,负数的幂是 ;
偶数
正数
1的奇次幂结果是 , 1的偶次幂结果是 .
1
1
归纳:
新知讲解
例2.用计算器计算( 8)5和( 3)6.
显示:(─ 8)∧5
─32768
显示:(─ 3)∧6
729.
所以( 8)5= 32768,( 3)6=729.
解:用带符号键 的计算器.
(─ 8)∧5
─32768
(─ 3)∧6
729
练一练
用计算器计算( 11)6和167.
显示:(─ 11)∧6
1771561
显示:16∧7
268435456
所以( 11)6=1771561,167=268435456
解:用带符号键 的计算器.
(─ 11)∧6
1771561
16∧7
268435456
课堂练习
1.下列说法正确的是( ).
读作 3的4次幂
B.的底数是 3,指数是4
C. 表示4个3相乘的积的相反数
D. 表示4个 3相乘的积
2.下列说法正确的是( ).
A. 25表示2×5
C. 32与( 3)2互为相反数
B. 25中2是底数,5是幂
D. a5=( a)5
C
C
课堂练习
3. 计算: 14的结果是( )
A. 1 B. 1 C. 4 D.4
4.规定一种新运算: ,如 .则 的值是( ).
A. B. C. 6 D.
B
C
课堂练习
5.下列各式中结果是负数的为( )
A. ( 5) B. ( 5)2
C. 52 D. | 5|
6. 在 ( 3), | 6|, ( 2)2 , 5这四个数中,比 4小的数是( )
A. ( 3) B. | 6|
C. ( 2)2 D. 5
C
B
课堂练习
7.你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示.这样捏合到第7次后可拉出 根细面条.
64
课堂练习
8.计算:
=( 5)╳( 5)╳( 5)
= 125
=( 3)╳( 3)╳( 3) ╳( 3)
=81
=()╳()╳()=
课堂练习
9. 规定两数a,b之间的一种运算,记作(a, b):如果那么(a,b)=c.例如:因为所以(2,8)=3
(1)根据上述规定,填空:(3,9)=________, (4,64)=________.
(2)(4,a)=2, (b,8)=3,= .
2
3
4
课堂总结
1.乘方的定义及表示的意义.
2.乘方的读法:① 读作的次方(看作运算)
② 读作的次幂(看作结果)
二.有理数乘方的运算:
当指数是 时,负数的幂是 ;
奇数
负数
正数的任何次幂都是 ;0的任何正整数次幂都是 .
正数
0
当指数是 时,负数的幂是 ;
偶数
正数
一.乘方
作业布置
习题1.5
第47第1题和第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
