北师大版八年级数学上册5.4应用二元一次方程组 增收节支 同步练习(含答案)
文档属性
| 名称 | 北师大版八年级数学上册5.4应用二元一次方程组 增收节支 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 00:00:00 | ||
图片预览


文档简介
北师大版八上 5.4 应用二元一次方程组-增收节支
一、选择题(共15小题)
1. 某班 名同学在植树节这天共种植了 棵树苗,其中男生每人种 棵,女生每人种 棵.设男生有 名,女生有 名,根据题意,列方程组正确的是
A. B. C. D.
2. 为了开展阳光体育活动,丰富同学们的课余生活,体育委员欧阳锋到体育用品商店购羽毛球拍和乒乓球拍,若购 副羽毛球拍和 副乒乓球拍共需 元,欧阳锋一共用 元购买了 副同样的羽毛球拍和 副同样的乒乓球拍,若设每副羽毛球拍为 元,每副乒乓球拍为 元,列二元一次方程组得
A. B.
C. D.
3. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长 尺;如果将绳索对半折后再去量竿,就比竿短 尺.设绳索长 尺,竿长 尺,则符合题意的方程组是
A. B. C. D.
4. 某木工厂有 人,一个工人每天可加工 张桌子或 只椅子, 张桌子与 只椅子配套,现要求工人每天做的桌子和椅子完整配套而没有剩余,若设安排 个工人加工桌子, 个工人加工椅子,则列出正确的二元一次方程组为
A. B. C. D.
5. 小明早上骑自行车上学,中途因道路施工步行一段路,到学校共用 分钟,他骑自行车的平均速度是 米/分,步行的速度是 米/分,他家离学校的距离是 米.设他骑自行车和步行的时间分别为 分钟,则列出的二元一次方程组是
A. B.
C. D.
6. 一船顺水航行 需要 ,逆水航行 需要 ,若设船在静水中的速度为 ,水流速度为 ,则 , 的值分别为
A. , B. , C. , D. ,
7. 甲、乙两人分别从相距 的两地同时出发,若同向而行,则 后,快者追上慢者;若相向而行,则 后,两个相遇,那么快者速度和慢者速度(单位:)分别是
A. 和 B. 和 C. 和 D. 和
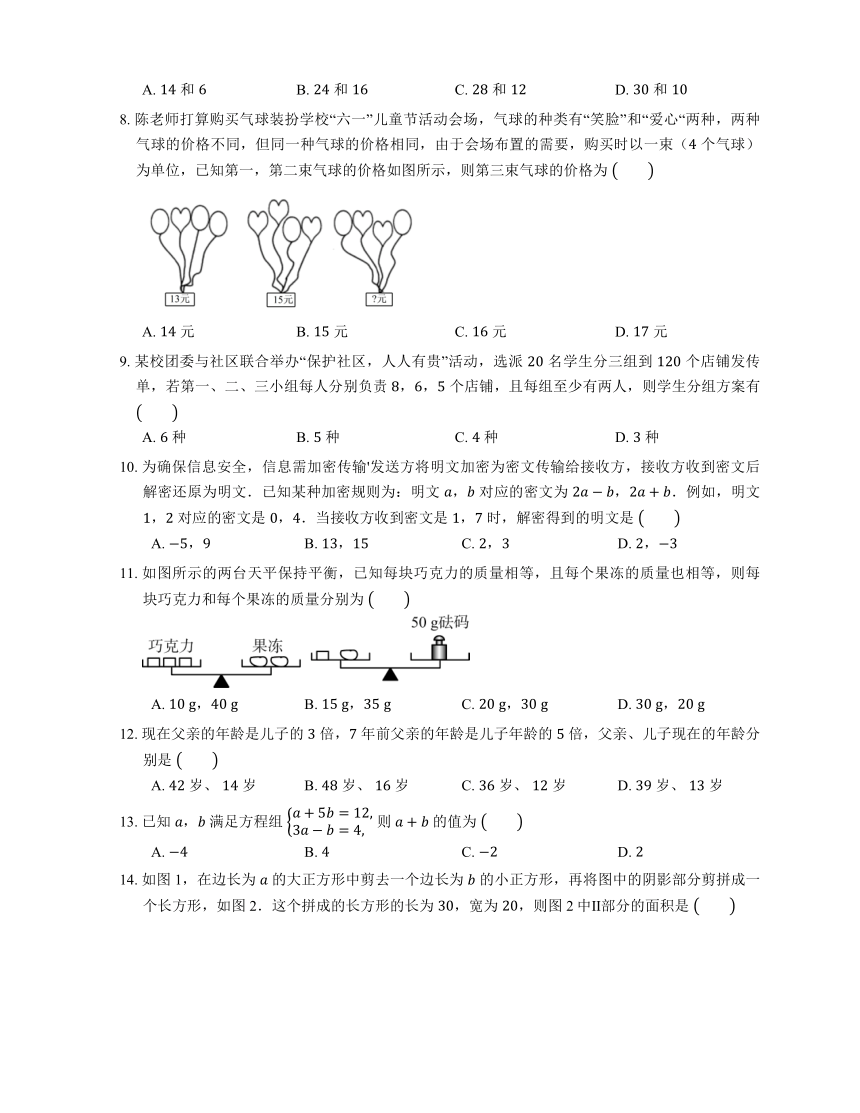
8. 陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有“笑脸”和“爱心“两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置的需要,购买时以一束( 个气球)为单位,已知第一,第二束气球的价格如图所示,则第三束气球的价格为
A. 元 B. 元 C. 元 D. 元
9. 某校团委与社区联合举办“保护社区,人人有贵”活动,选派 名学生分三组到 个店铺发传单,若第一、二、三小组每人分别负责 ,, 个店铺,且每组至少有两人,则学生分组方案有
A. 种 B. 种 C. 种 D. 种
10. 为确保信息安全,信息需加密传输'发送方将明文加密为密文传输给接收方,接收方收到密文后解密还原为明文.已知某种加密规则为:明文 , 对应的密文为 ,.例如,明文 , 对应的密文是 ,.当接收方收到密文是 , 时,解密得到的明文是
A. , B. , C. , D. ,
11. 如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为
A. , B. , C. , D. ,
12. 现在父亲的年龄是儿子的 倍, 年前父亲的年龄是儿子年龄的 倍,父亲、儿子现在的年龄分别是
A. 岁、 岁 B. 岁、 岁 C. 岁、 岁 D. 岁、 岁
13. 已知 , 满足方程组 则 的值为
A. B. C. D.
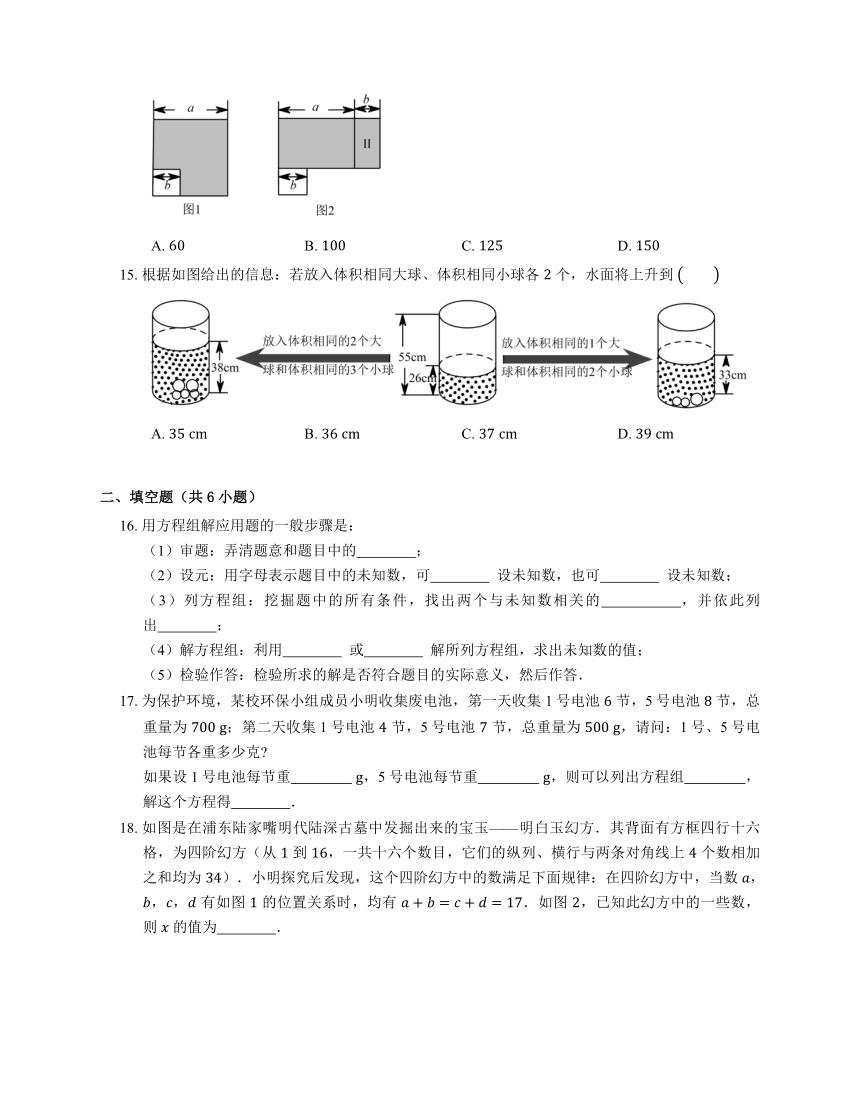
14. 如图1,在边长为 的大正方形中剪去一个边长为 的小正方形,再将图中的阴影部分剪拼成一个长方形,如图2.这个拼成的长方形的长为 ,宽为 ,则图2中Ⅱ部分的面积是
A. B. C. D.
15. 根据如图给出的信息:若放入体积相同大球、体积相同小球各 个,水面将上升到
A. B. C. D.
二、填空题(共6小题)
16. 用方程组解应用题的一般步骤是:
(1)审题:弄清题意和题目中的 ;
(2)设元:用字母表示题目中的未知数,可 设未知数,也可 设未知数;
(3)列方程组:挖掘题中的所有条件,找出两个与未知数相关的 ,并依此列出 ;
(4)解方程组:利用 或 解所列方程组,求出未知数的值;
(5)检验作答:检验所求的解是否符合题目的实际意义,然后作答.
17. 为保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池 节,5号电池 节,总重量为 ;第二天收集1号电池 节,5号电池 节,总重量为 ,请问:1号、5号电池每节各重多少克
如果设1号电池每节重 ,5号电池每节重 ,则可以列出方程组 ,解这个方程得 .
18. 如图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉——明白玉幻方.其背面有方框四行十六格,为四阶幻方(从 到 ,一共十六个数目,它们的纵列、横行与两条对角线上 个数相加之和均为 ).小明探究后发现,这个四阶幻方中的数满足下面规律:在四阶幻方中,当数 ,,, 有如图 的位置关系时,均有 .如图 ,已知此幻方中的一些数,则 的值为 .
19. 如图,将长方形 分割成 个灰色长方形与 个面积相等的小正方形.若灰色长方形的长与宽之比为 ,则 .
20. 清明节期间,七(1)班全体同学分成若干小组到革命传统教育基地缅怀先烈.若每小组 人,则余下 人;若每小组 人,则少 人,由此可知该班共有 名同学.
21. 某地准备对一段长 的河道进行清淤疏通.若甲工程队先用 天单独完成其中一部分河道的疏通任务,则余下的任务由乙工程队单独完成需要 天;若甲工程队先单独工作 天,则余下的任务由乙工程队单独完成需要 天.设甲工程队平均每天疏通河道 ,乙工程队平均每天疏通河道 ,则 的值为 .
三、解答题(共5小题)
22. 上杭教育服装厂要生产一批某种型号的学生服装,已知 米长的布料可做上衣 件或裤子 条,一件上衣和一条裤子为一套,计划用 米长的这种布料生产,应分别用多少布料生产上衣和裤子才能恰好配套 共能生产多少套
23. 在长为 ,宽为 的矩形空地中,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,其示意图如图所示.求小矩形花圃的长和宽.
24. 老王有一批货物要从 地运往 地,准备租用某汽车运输公司的甲、乙两种货车若干辆.经了解,这两种货车两次运载货物的情况如下表(每次都是满载):
(1)甲、乙两种货车每辆各可运货物多少吨
(2)现老王租用该公司甲货车 辆,乙货车 辆,刚好将这批货物运完(满载).若每吨货的运费为 元,则老王应付运输费多少元
25. 月 日,某中学组织全校学生参加“学习雷锋,服务社会”的活动.六年级()班全体同学分为三组参加打扫绿化带、去敬老院服务和到社区文艺演出的活动.小明和小丽同学统计了当天本班学生参加三项活动的人数,并各自绘制以下两张图.请根据这两张图中提供的信息解答下列问题:
(1)六年级()班共有 名学生;
(2)请帮助小明补全条形统计图的空缺部分;
(3)小丽绘制的扇形统计图中表示“去敬老院服务”的扇形的圆心角是 .
26. 实验表明,某种气体的体积 ()随着温度 ()的改变而改变,它的体积可用公式 计算.已测得当 时,体积 ;当 时,.求:
(1), 的值.
(2)当温度为 时该气体的体积.
答案
1. D
2. A
3. A
4. A
5. D
【解析】设他骑自行车和步行的时间分别为 分钟,由题意得
6. B
7. A
8. A
【解析】设每个“笑脸”和“爱心“分别为 、 元.
由题意可得:
.
第三束气球的价格为 元.
9. B
【解析】设第一小组有 人,第二小组有 人,则第三小组有 人.
则 ,即 .
当 ,,,, 时,都符合题意,
所以共有 种方案.
10. C
【解析】题意列方程组,得 解得 ,.
11. C
【解析】设每块巧克力和每个果冻的质量分别为 克, 克.
由题意可得
解得
12. A
【解析】设父亲现在的年龄是 岁,儿子现在的年龄是 岁.
由题意得
解得
13. B
【解析】
得 ,即 ,把 代入 得 ,则 .
14. B
15. B
16. (1)数量关系,(2)直接,间接,(3)等量关系,方程组,(4)代入消元法,加减消元法
17. ,,,
18.
19.
【解析】设灰色长方形的长上摆 个小正方形,宽上摆 个小正方形.
解得
,.
20.
【解析】设该班有 人,一共有 组.
根据题意,得
21.
【解析】由题意可列方程组
两式相加得
.
22. 设用 米布料生产上衣, 米布料生产裤子才能配套,
则
解得
答:用 米生产上衣, 米生产裤子才能配套,共能生产 套.
23. 设小矩形的长为 ,宽为 ,由题意得:
解得:
答:小矩形的长为 ,宽为 .
24. (1) 设甲、乙两种货车每辆各运货物 吨与 吨.
得
解得
(2) (元).
所以,老王应付运输费 元.
25. (1)
(2) 人(图略).
(3)
26. (1) 由题意可列方程
解得
(2) 由(1)可知: .
当 时,.
一、选择题(共15小题)
1. 某班 名同学在植树节这天共种植了 棵树苗,其中男生每人种 棵,女生每人种 棵.设男生有 名,女生有 名,根据题意,列方程组正确的是
A. B. C. D.
2. 为了开展阳光体育活动,丰富同学们的课余生活,体育委员欧阳锋到体育用品商店购羽毛球拍和乒乓球拍,若购 副羽毛球拍和 副乒乓球拍共需 元,欧阳锋一共用 元购买了 副同样的羽毛球拍和 副同样的乒乓球拍,若设每副羽毛球拍为 元,每副乒乓球拍为 元,列二元一次方程组得
A. B.
C. D.
3. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长 尺;如果将绳索对半折后再去量竿,就比竿短 尺.设绳索长 尺,竿长 尺,则符合题意的方程组是
A. B. C. D.
4. 某木工厂有 人,一个工人每天可加工 张桌子或 只椅子, 张桌子与 只椅子配套,现要求工人每天做的桌子和椅子完整配套而没有剩余,若设安排 个工人加工桌子, 个工人加工椅子,则列出正确的二元一次方程组为
A. B. C. D.
5. 小明早上骑自行车上学,中途因道路施工步行一段路,到学校共用 分钟,他骑自行车的平均速度是 米/分,步行的速度是 米/分,他家离学校的距离是 米.设他骑自行车和步行的时间分别为 分钟,则列出的二元一次方程组是
A. B.
C. D.
6. 一船顺水航行 需要 ,逆水航行 需要 ,若设船在静水中的速度为 ,水流速度为 ,则 , 的值分别为
A. , B. , C. , D. ,
7. 甲、乙两人分别从相距 的两地同时出发,若同向而行,则 后,快者追上慢者;若相向而行,则 后,两个相遇,那么快者速度和慢者速度(单位:)分别是
A. 和 B. 和 C. 和 D. 和
8. 陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有“笑脸”和“爱心“两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置的需要,购买时以一束( 个气球)为单位,已知第一,第二束气球的价格如图所示,则第三束气球的价格为
A. 元 B. 元 C. 元 D. 元
9. 某校团委与社区联合举办“保护社区,人人有贵”活动,选派 名学生分三组到 个店铺发传单,若第一、二、三小组每人分别负责 ,, 个店铺,且每组至少有两人,则学生分组方案有
A. 种 B. 种 C. 种 D. 种
10. 为确保信息安全,信息需加密传输'发送方将明文加密为密文传输给接收方,接收方收到密文后解密还原为明文.已知某种加密规则为:明文 , 对应的密文为 ,.例如,明文 , 对应的密文是 ,.当接收方收到密文是 , 时,解密得到的明文是
A. , B. , C. , D. ,
11. 如图所示的两台天平保持平衡,已知每块巧克力的质量相等,且每个果冻的质量也相等,则每块巧克力和每个果冻的质量分别为
A. , B. , C. , D. ,
12. 现在父亲的年龄是儿子的 倍, 年前父亲的年龄是儿子年龄的 倍,父亲、儿子现在的年龄分别是
A. 岁、 岁 B. 岁、 岁 C. 岁、 岁 D. 岁、 岁
13. 已知 , 满足方程组 则 的值为
A. B. C. D.
14. 如图1,在边长为 的大正方形中剪去一个边长为 的小正方形,再将图中的阴影部分剪拼成一个长方形,如图2.这个拼成的长方形的长为 ,宽为 ,则图2中Ⅱ部分的面积是
A. B. C. D.
15. 根据如图给出的信息:若放入体积相同大球、体积相同小球各 个,水面将上升到
A. B. C. D.
二、填空题(共6小题)
16. 用方程组解应用题的一般步骤是:
(1)审题:弄清题意和题目中的 ;
(2)设元:用字母表示题目中的未知数,可 设未知数,也可 设未知数;
(3)列方程组:挖掘题中的所有条件,找出两个与未知数相关的 ,并依此列出 ;
(4)解方程组:利用 或 解所列方程组,求出未知数的值;
(5)检验作答:检验所求的解是否符合题目的实际意义,然后作答.
17. 为保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池 节,5号电池 节,总重量为 ;第二天收集1号电池 节,5号电池 节,总重量为 ,请问:1号、5号电池每节各重多少克
如果设1号电池每节重 ,5号电池每节重 ,则可以列出方程组 ,解这个方程得 .
18. 如图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉——明白玉幻方.其背面有方框四行十六格,为四阶幻方(从 到 ,一共十六个数目,它们的纵列、横行与两条对角线上 个数相加之和均为 ).小明探究后发现,这个四阶幻方中的数满足下面规律:在四阶幻方中,当数 ,,, 有如图 的位置关系时,均有 .如图 ,已知此幻方中的一些数,则 的值为 .
19. 如图,将长方形 分割成 个灰色长方形与 个面积相等的小正方形.若灰色长方形的长与宽之比为 ,则 .
20. 清明节期间,七(1)班全体同学分成若干小组到革命传统教育基地缅怀先烈.若每小组 人,则余下 人;若每小组 人,则少 人,由此可知该班共有 名同学.
21. 某地准备对一段长 的河道进行清淤疏通.若甲工程队先用 天单独完成其中一部分河道的疏通任务,则余下的任务由乙工程队单独完成需要 天;若甲工程队先单独工作 天,则余下的任务由乙工程队单独完成需要 天.设甲工程队平均每天疏通河道 ,乙工程队平均每天疏通河道 ,则 的值为 .
三、解答题(共5小题)
22. 上杭教育服装厂要生产一批某种型号的学生服装,已知 米长的布料可做上衣 件或裤子 条,一件上衣和一条裤子为一套,计划用 米长的这种布料生产,应分别用多少布料生产上衣和裤子才能恰好配套 共能生产多少套
23. 在长为 ,宽为 的矩形空地中,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,其示意图如图所示.求小矩形花圃的长和宽.
24. 老王有一批货物要从 地运往 地,准备租用某汽车运输公司的甲、乙两种货车若干辆.经了解,这两种货车两次运载货物的情况如下表(每次都是满载):
(1)甲、乙两种货车每辆各可运货物多少吨
(2)现老王租用该公司甲货车 辆,乙货车 辆,刚好将这批货物运完(满载).若每吨货的运费为 元,则老王应付运输费多少元
25. 月 日,某中学组织全校学生参加“学习雷锋,服务社会”的活动.六年级()班全体同学分为三组参加打扫绿化带、去敬老院服务和到社区文艺演出的活动.小明和小丽同学统计了当天本班学生参加三项活动的人数,并各自绘制以下两张图.请根据这两张图中提供的信息解答下列问题:
(1)六年级()班共有 名学生;
(2)请帮助小明补全条形统计图的空缺部分;
(3)小丽绘制的扇形统计图中表示“去敬老院服务”的扇形的圆心角是 .
26. 实验表明,某种气体的体积 ()随着温度 ()的改变而改变,它的体积可用公式 计算.已测得当 时,体积 ;当 时,.求:
(1), 的值.
(2)当温度为 时该气体的体积.
答案
1. D
2. A
3. A
4. A
5. D
【解析】设他骑自行车和步行的时间分别为 分钟,由题意得
6. B
7. A
8. A
【解析】设每个“笑脸”和“爱心“分别为 、 元.
由题意可得:
.
第三束气球的价格为 元.
9. B
【解析】设第一小组有 人,第二小组有 人,则第三小组有 人.
则 ,即 .
当 ,,,, 时,都符合题意,
所以共有 种方案.
10. C
【解析】题意列方程组,得 解得 ,.
11. C
【解析】设每块巧克力和每个果冻的质量分别为 克, 克.
由题意可得
解得
12. A
【解析】设父亲现在的年龄是 岁,儿子现在的年龄是 岁.
由题意得
解得
13. B
【解析】
得 ,即 ,把 代入 得 ,则 .
14. B
15. B
16. (1)数量关系,(2)直接,间接,(3)等量关系,方程组,(4)代入消元法,加减消元法
17. ,,,
18.
19.
【解析】设灰色长方形的长上摆 个小正方形,宽上摆 个小正方形.
解得
,.
20.
【解析】设该班有 人,一共有 组.
根据题意,得
21.
【解析】由题意可列方程组
两式相加得
.
22. 设用 米布料生产上衣, 米布料生产裤子才能配套,
则
解得
答:用 米生产上衣, 米生产裤子才能配套,共能生产 套.
23. 设小矩形的长为 ,宽为 ,由题意得:
解得:
答:小矩形的长为 ,宽为 .
24. (1) 设甲、乙两种货车每辆各运货物 吨与 吨.
得
解得
(2) (元).
所以,老王应付运输费 元.
25. (1)
(2) 人(图略).
(3)
26. (1) 由题意可列方程
解得
(2) 由(1)可知: .
当 时,.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
