人教版九年级数学上册第25章概率初步单元综合训练(含答案)
文档属性
| 名称 | 人教版九年级数学上册第25章概率初步单元综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 353.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 09:34:12 | ||
图片预览



文档简介
2022-2023学年人教版九年级数学上册
第25章《概率初步》综合训练
一、单选题
1.如图是用七巧板拼成的正方形桌面,一个小球在桌面上自由地滚动,它最终停在黑色区域的概率是( )
A. B. C. D.
2.分别向如图所示的四个区域投掷一个小球,小球落在阴影部分的概率最小的是( )
A. B. C. D.
3.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是( )
A. B. C. D.
4.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.
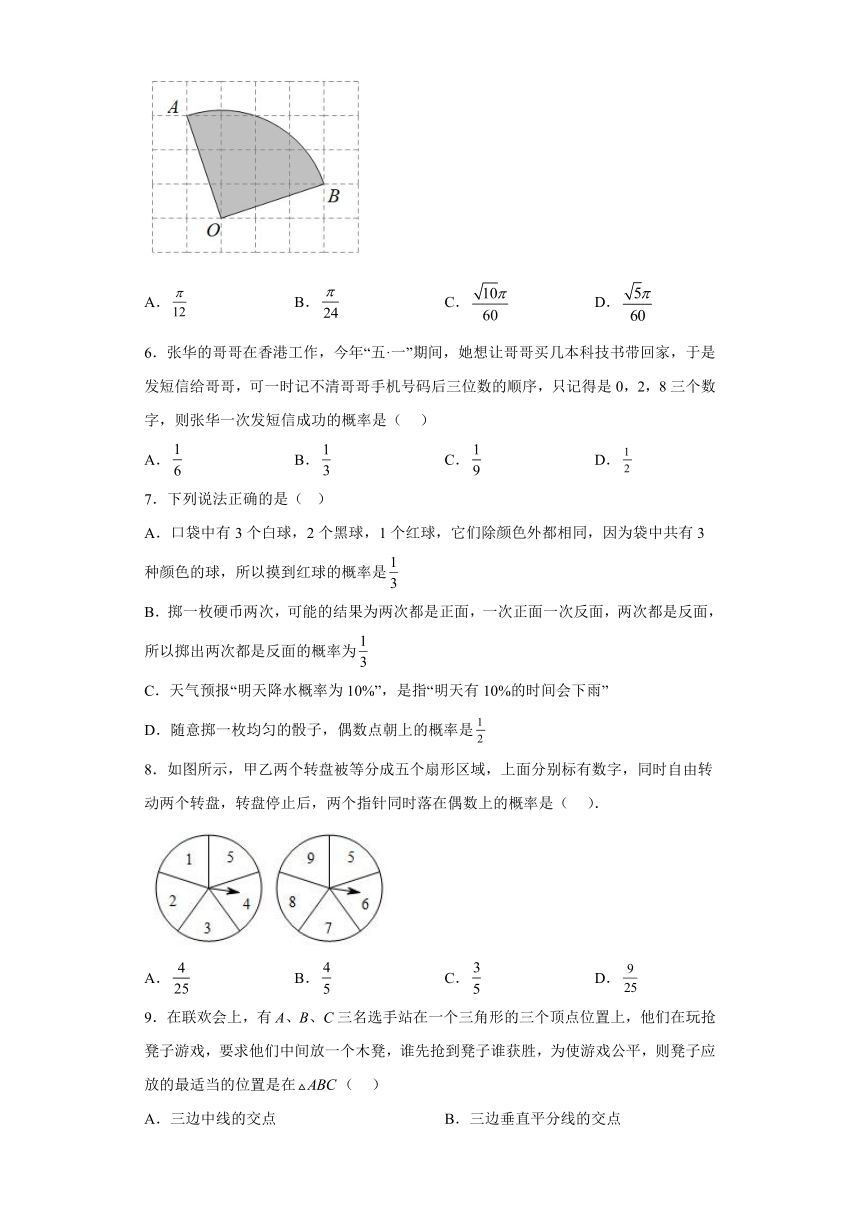
5.如图,在的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )
A. B. C. D.
6.张华的哥哥在香港工作,今年“五·一”期间,她想让哥哥买几本科技书带回家,于是发短信给哥哥,可一时记不清哥哥手机号码后三位数的顺序,只记得是0,2,8三个数字,则张华一次发短信成功的概率是( )
A. B. C. D.
7.下列说法正确的是( )
A.口袋中有3个白球,2个黑球,1个红球,它们除颜色外都相同,因为袋中共有3种颜色的球,所以摸到红球的概率是
B.掷一枚硬币两次,可能的结果为两次都是正面,一次正面一次反面,两次都是反面,所以掷出两次都是反面的概率为
C.天气预报“明天降水概率为10%”,是指“明天有10%的时间会下雨”
D.随意掷一枚均匀的骰子,偶数点朝上的概率是
8.如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,两个指针同时落在偶数上的概率是( ).
A. B. C. D.
9.在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在( )
A.三边中线的交点 B.三边垂直平分线的交点
C.三条角平分线的交点 D.三边上高的交点
10.某小组做“用频率估计概率”的试验时,统计了某结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小时随机出的是“剪刀”
B.袋子中有1个红球和2个黄球,从中任取一球是黄球
C.掷一个质地均匀的正六面体骰子,向上的面点数是偶数
D.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌花色是红桃
二、填空题
11.如图,四条直径把两个同心圆分成八等份,若往圆面投掷飞镖,则飞镖落在白色区域的概率是____.
12.在,,,,,中任取一个数,取到无理数的概率是______ .
13.小兰和小华两人做游戏,她们准备了一个质地均匀的正六面体骰子,骰子的六个面分别标有1,2,3,4,5,6,若掷出的骰子的点数为偶数,则小兰赢;若掷出的骰子的点数是3的倍数,则小华赢,游戏规则对______(填“小兰”或“小华”)有利.
14.不透明的袋子中装有4个红球、3个黄球和5个蓝球,每个球除颜色不同外其他都相同,从中任意摸出一个球_____球的可能性最大.
15.如图所示,准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形.将这三张纸片放在一个盒子里摇匀,随机地抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张画有正方形)则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?___________________________.
三、解答题
16.一个不透明的口袋里装有分别标有汉字“书”、“香”、“历”、“城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是“书”的概率为 .
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
17.一个批发商从某服装制造公司购进了50包型号为L的衬衫,由于包装工人疏忽,在包裹中混进了型号为M的衬衫.每包中混入的M号衬衫数见下页表:
M号衬衫数 0 1 4 5 7 9 10 11
包数 7 3 10 15 5 4 3 3
一位零售商从50包中任意选取了一包,求下列事件的概率:
(1)包中没有混入M号衬衫;
(2)包中混入M号衬衫数不超过7;
(3)包中混入M号衬衫数超过10.
18.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的小球共20只.某学习小组做摸球试验,将球搅匀后从中随机摸出一球记下颜色,再把它放回袋里,不断重复,下表是活动进行中的一组统计数据:表
摸球的次数 100 150 200 500 800 1000
摸到白球的次数n 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的概率将会接近 (精确到0.1)
(2)假如你去摸一次,你摸到白球的概率 ,摸到黑球的概率 .
(3)试估算口袋中黑、白两种颜色的球各有多少只?
19.一场数学游戏在两个非常聪明的学生甲、乙之间进行,裁判在黑板上写出正整数2,3,4,…,2006,然后随意擦去一个数,接下来由甲、乙两人轮流擦去其中一个数(即乙先擦去其中一个数,然后甲再擦去一个数).如此下去,若最后剩下的两个数互素,则判甲胜;否则,判乙胜,按照这种游戏规则,求甲获胜的概率(用具体数字作答).
20.某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),根据统计图提供的信息,回答问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;
(2)补全条形统计图;扇形统计图中,成绩为10分的所在扇形的圆心角是 度;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
参考答案
1.C
2.A
3.A
4.A
5.A
6.A
7.D
8.A
9.B
10.C
11.
12.
13.小兰
14.摸出蓝球的概率大
15.不公平,乙有利
16.解:(1)若从中任取一个球,球上的汉字刚好是“书”的概率为,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果数,其中取出的两个球上的汉字能组成“历城”的结果数为,
所以取出的两个球上的汉字能组成“历城”的概率.
17.解:(1)P(没混入M号衬衫)=.
(2)P(混入的M号衬衫数不超过7)==.
(3)P(混入的M号衬衫数超过10)=.
18.解:(1)当n很大时,摸到白球的频率将会接近(0.58+0.64+0.58+0.59+0.605+0.601)÷6≈0.60,
故答案为:0.60;
(2)摸到白球的概率是0.60,摸到黑球的概率是1-0.60=0.40,
故答案为0.60,0.40;
(3)白球有20×0.60=12(只),黑球有20-12=8(只),
答:黑、白两种颜色的球各有8只、12只.
19.解 获胜的关键,要看裁判擦去的是奇数还是偶数,注意到2,3,4,…,2006中有1003个偶数,1002个奇数.
(1)若裁判擦去的是奇数,则乙一定获胜.
乙不管甲擦去什么数,只要有奇数,乙就擦去奇数(没有奇数时才擦去偶数)这样最后两个数一定都是偶数,它们不互素,故乙胜.
(2)若裁判擦去的是偶数,则所剩的2004个数可配成1002对,每对中两个数互补:,,…,,,…,
这样不管乙擦去哪个数,甲都擦去所配对中另一个数,最后剩下的两数必然是配成一对的两个数,它们互补,故甲胜.
所以,甲获胜的概率为.
20.解:(1)校毕业生中男生有:20+40+60+180=300人.
∵100%=12%,
∴a=12.
故答案为300,12.
(2)由题意b=1﹣10%﹣12%﹣16%=62%,
∴成绩为10分的所在扇形的圆心角是360°×62%=223.2°.
故答案为:223.2°,
500×62%﹣180=130人,
∵500×10%=50,
∴女生人数=50﹣20=30人.
条形图如图所示:
(3)这名学生该项成绩在8分及8分以下的概率是.
第25章《概率初步》综合训练
一、单选题
1.如图是用七巧板拼成的正方形桌面,一个小球在桌面上自由地滚动,它最终停在黑色区域的概率是( )
A. B. C. D.
2.分别向如图所示的四个区域投掷一个小球,小球落在阴影部分的概率最小的是( )
A. B. C. D.
3.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是( )
A. B. C. D.
4.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
A. B. C. D.
5.如图,在的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )
A. B. C. D.
6.张华的哥哥在香港工作,今年“五·一”期间,她想让哥哥买几本科技书带回家,于是发短信给哥哥,可一时记不清哥哥手机号码后三位数的顺序,只记得是0,2,8三个数字,则张华一次发短信成功的概率是( )
A. B. C. D.
7.下列说法正确的是( )
A.口袋中有3个白球,2个黑球,1个红球,它们除颜色外都相同,因为袋中共有3种颜色的球,所以摸到红球的概率是
B.掷一枚硬币两次,可能的结果为两次都是正面,一次正面一次反面,两次都是反面,所以掷出两次都是反面的概率为
C.天气预报“明天降水概率为10%”,是指“明天有10%的时间会下雨”
D.随意掷一枚均匀的骰子,偶数点朝上的概率是
8.如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,两个指针同时落在偶数上的概率是( ).
A. B. C. D.
9.在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在( )
A.三边中线的交点 B.三边垂直平分线的交点
C.三条角平分线的交点 D.三边上高的交点
10.某小组做“用频率估计概率”的试验时,统计了某结果出现的频率,绘制了如图的折线统计图,则符合这一结果的试验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小时随机出的是“剪刀”
B.袋子中有1个红球和2个黄球,从中任取一球是黄球
C.掷一个质地均匀的正六面体骰子,向上的面点数是偶数
D.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌花色是红桃
二、填空题
11.如图,四条直径把两个同心圆分成八等份,若往圆面投掷飞镖,则飞镖落在白色区域的概率是____.
12.在,,,,,中任取一个数,取到无理数的概率是______ .
13.小兰和小华两人做游戏,她们准备了一个质地均匀的正六面体骰子,骰子的六个面分别标有1,2,3,4,5,6,若掷出的骰子的点数为偶数,则小兰赢;若掷出的骰子的点数是3的倍数,则小华赢,游戏规则对______(填“小兰”或“小华”)有利.
14.不透明的袋子中装有4个红球、3个黄球和5个蓝球,每个球除颜色不同外其他都相同,从中任意摸出一个球_____球的可能性最大.
15.如图所示,准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形.将这三张纸片放在一个盒子里摇匀,随机地抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形)则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张画有正方形)则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?___________________________.
三、解答题
16.一个不透明的口袋里装有分别标有汉字“书”、“香”、“历”、“城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是“书”的概率为 .
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
17.一个批发商从某服装制造公司购进了50包型号为L的衬衫,由于包装工人疏忽,在包裹中混进了型号为M的衬衫.每包中混入的M号衬衫数见下页表:
M号衬衫数 0 1 4 5 7 9 10 11
包数 7 3 10 15 5 4 3 3
一位零售商从50包中任意选取了一包,求下列事件的概率:
(1)包中没有混入M号衬衫;
(2)包中混入M号衬衫数不超过7;
(3)包中混入M号衬衫数超过10.
18.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的小球共20只.某学习小组做摸球试验,将球搅匀后从中随机摸出一球记下颜色,再把它放回袋里,不断重复,下表是活动进行中的一组统计数据:表
摸球的次数 100 150 200 500 800 1000
摸到白球的次数n 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的概率将会接近 (精确到0.1)
(2)假如你去摸一次,你摸到白球的概率 ,摸到黑球的概率 .
(3)试估算口袋中黑、白两种颜色的球各有多少只?
19.一场数学游戏在两个非常聪明的学生甲、乙之间进行,裁判在黑板上写出正整数2,3,4,…,2006,然后随意擦去一个数,接下来由甲、乙两人轮流擦去其中一个数(即乙先擦去其中一个数,然后甲再擦去一个数).如此下去,若最后剩下的两个数互素,则判甲胜;否则,判乙胜,按照这种游戏规则,求甲获胜的概率(用具体数字作答).
20.某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),根据统计图提供的信息,回答问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;
(2)补全条形统计图;扇形统计图中,成绩为10分的所在扇形的圆心角是 度;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
参考答案
1.C
2.A
3.A
4.A
5.A
6.A
7.D
8.A
9.B
10.C
11.
12.
13.小兰
14.摸出蓝球的概率大
15.不公平,乙有利
16.解:(1)若从中任取一个球,球上的汉字刚好是“书”的概率为,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果数,其中取出的两个球上的汉字能组成“历城”的结果数为,
所以取出的两个球上的汉字能组成“历城”的概率.
17.解:(1)P(没混入M号衬衫)=.
(2)P(混入的M号衬衫数不超过7)==.
(3)P(混入的M号衬衫数超过10)=.
18.解:(1)当n很大时,摸到白球的频率将会接近(0.58+0.64+0.58+0.59+0.605+0.601)÷6≈0.60,
故答案为:0.60;
(2)摸到白球的概率是0.60,摸到黑球的概率是1-0.60=0.40,
故答案为0.60,0.40;
(3)白球有20×0.60=12(只),黑球有20-12=8(只),
答:黑、白两种颜色的球各有8只、12只.
19.解 获胜的关键,要看裁判擦去的是奇数还是偶数,注意到2,3,4,…,2006中有1003个偶数,1002个奇数.
(1)若裁判擦去的是奇数,则乙一定获胜.
乙不管甲擦去什么数,只要有奇数,乙就擦去奇数(没有奇数时才擦去偶数)这样最后两个数一定都是偶数,它们不互素,故乙胜.
(2)若裁判擦去的是偶数,则所剩的2004个数可配成1002对,每对中两个数互补:,,…,,,…,
这样不管乙擦去哪个数,甲都擦去所配对中另一个数,最后剩下的两数必然是配成一对的两个数,它们互补,故甲胜.
所以,甲获胜的概率为.
20.解:(1)校毕业生中男生有:20+40+60+180=300人.
∵100%=12%,
∴a=12.
故答案为300,12.
(2)由题意b=1﹣10%﹣12%﹣16%=62%,
∴成绩为10分的所在扇形的圆心角是360°×62%=223.2°.
故答案为:223.2°,
500×62%﹣180=130人,
∵500×10%=50,
∴女生人数=50﹣20=30人.
条形图如图所示:
(3)这名学生该项成绩在8分及8分以下的概率是.
同课章节目录
