2022—2023学年度华东师大版数学九年级册第27章圆达标测试卷 (含解析)
文档属性
| 名称 | 2022—2023学年度华东师大版数学九年级册第27章圆达标测试卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 278.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 00:00:00 | ||
图片预览




文档简介
圆 达标测试卷
一、选择题(每题3分,共24分)
1.⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5 B.6 C.7 D.8
2.如图,在⊙O中,=,∠1=45°,则∠2的度数为( )
A.60° B.30°
C.45° D.40°
(第2题) (第3题)
3.如图,PA,PB分别切⊙O于A,B两点,如果∠P=60°,PA=2,那么△PAB的周长为( )
A.2 B.6 C.7 D.4
4.已知圆锥的母线长为6 cm,底面圆的半径为3 cm,则此圆锥侧面展开图(扇形)的圆心角是( )
A.30° B.60°
C.90° D.180°
5.如图,已知⊙O中,∠AOB=100°,则∠ACB的度数是( )
A.50° B.100°
C.120° D.130°
(第5题) (第6题)
6.如图,△ABC是⊙O的内接三角形,AB=2 ,∠ACB=60°,连结OA,OB,则的长是( )
A. B. C.π D.
7.如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=2OE,则∠BCD的度数为( )
A.15° B.22.5° C.30° D.45°
(第7题) (第8题)
8.如图,等腰三角形ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AB=AC=5,BC=6,则DE的长是( )
A. B. C. D.
二、填空题(每题3分,共18分)
9.已知⊙O的半径是3 cm,点O到直线l的距离为4 cm,则⊙O与直线l的位置关系是__________.
10.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是________.
(第10题) (第11题)
11.如图,AB为⊙O的直径,∠ABC=36°,当∠BCD=______°时,CD为⊙O的切线.
12.如图,等边三角形ABC内接于半径为1的⊙O,则图中阴影部分的面积是________.
(第12题) (第13题)
13.如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是________.
14.如图,在平面直角坐标系中,点A(-6,8),B(-6,0),以A为圆心,4为半径作⊙A,点P为⊙A上一动点,M为OP的中点,连接BM,设BM的最大值为m,最小值为n,则m-n的值为________.
(第14题)
三、解答题(15题8分,16~20题每题10分,共58分)
15.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连结AD,BC,求证:
(1)=;
(2)AE=CE.
(第15题)
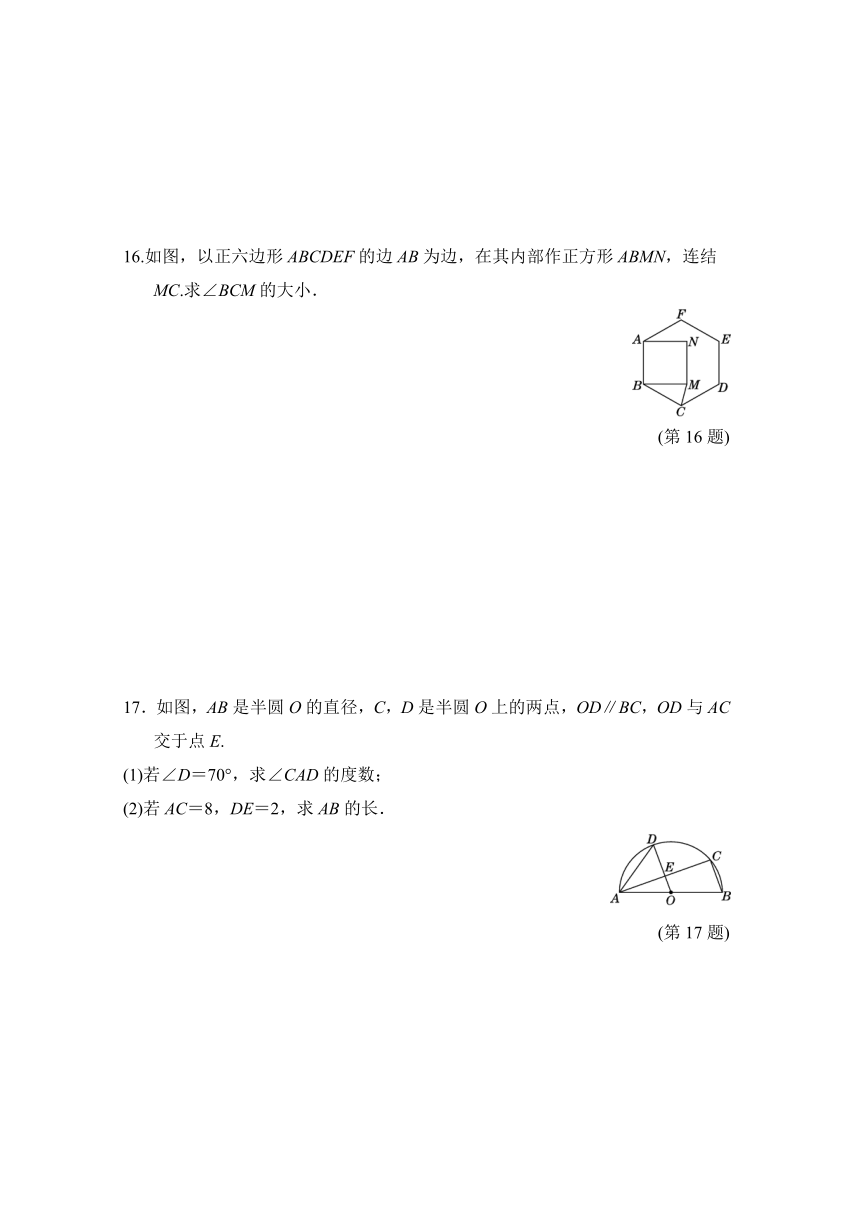
16.如图,以正六边形ABCDEF的边AB为边,在其内部作正方形ABMN,连结MC.求∠BCM的大小.
(第16题)
17.如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.
(1)若∠D=70°,求∠CAD的度数;
(2)若AC=8,DE=2,求AB的长.
(第17题)
18.如图,在半径为5的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,E是BC的中点,OE=3.
(1)求证:CD是⊙O的切线;
(2)求AD的长.
(第18题)
19.如图,⊙O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作⊙O的切线交A1A11的延长线于点P.
(1)通过计算比较直径和劣弧A7A11的长度哪个更长;
(2)连结A7A11,则A7A11和PA1有什么特殊的位置关系?请简要说明理由;
(3)求PA7的长.
(第19题)
20.在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连结一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.小明受此启发设计了一个“双连杆机构”,设计图如图①,两个固定长度的“连杆”AP,BP的连结点P在⊙O上,当点P在⊙O上转动时,带动点A,B分别在射线OM,ON上滑动,OM⊥ON.当AP与⊙O相切时,点B恰好落在⊙O上,如图②.
请仅就图②的情形解答下列问题.
(1)求证:∠PAO=2∠PBO;
(2)若⊙O的半径为5,AP=,求BP的长.
(第20题)
答案
一、1.A 2.C 3.B 4.D 5.D
6.D 点拨:过点O作OD⊥AB于点D,
则AD=DB=AB=,∠AOD=∠AOB,
由圆周角定理,得∠AOB=2∠ACB=120°,
∴∠AOD=60°,∴OA===2,
∴的长为=.
7.B
8.D 点拨:连结OA,OE,OB,OD,OB交DE于点H,如图.
(第8题)
∵等腰三角形ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,∴AO平分∠BAC,OE⊥BC,OD⊥AB,BE=BD.∵AB=AC,∴AO⊥BC,∴点A,O,E共线,即AE⊥BC,
∴BE=CE=3.
在Rt△ABE中,AE===4.
∵BD=BE=3,∴AD=2.
设⊙O的半径为r,则OD=OE=r,AO=4-r,
在Rt△AOD中,r2+22=(4-r)2,解得r=.
在Rt△BOE中,OB==.
∵BD=BE,OD=OE,∴OB垂直平分DE,∴DH=EH.
易得HE·OB=OE·BE,
∴HE===,
∴DE=2EH=.故选D.
二、9.相离 10.6 11.54 12.π-
13.(-,1) 点拨:∵四边形ABOC为圆的内接四边形,
∴∠ABO+∠ACO=180°.∵∠ACO=120°,
∴∠ABO=180°-120°=60°.
∵∠AOB=90°,∴AB为⊙D的直径,
∴D为AB的中点.
在Rt△ABO中,∵∠ABO=60°,
∴OB=AB=2,OA=AB·sin 60°=2 ,
∴A(-2 ,0),B(0,2),
∴点D的坐标为(-,1).
14.4
三、15.证明:(1)∵AB=CD,∴=,
∴+=+,∴=.
(2)∵=,∴AD=BC.
∵∠ADE=∠CBE,∠AED=∠CEB,
∴△ADE≌△CBE,∴AE=EC.
16.解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90°,AB=BM.
∴∠MBC=120°-90°=30°,BM=BC.
∴∠BCM=∠BMC.∴∠BCM=×(180°-30°)=75°.
17.解:(1)∵OA=OD,∠D=70°,∴∠OAD=∠D=70°,
∴∠AOD=180°-∠OAD-∠D=40°.
∵AB是半圆O的直径,∴∠C=90°.
∵OD∥BC,∴∠AEO=∠C=90°,即OD⊥AC.
∴=,∴∠CAD=∠AOD=20°.
(2)由(1)可知OD⊥AC,
∴AE=AC=×8=4.
设OA=x,则OE=OD-DE=x-2.
在Rt△OAE中,OE2+AE2=OA2,
即(x-2)2+42=x2,解得x=5.
∴AB=2OA=10.
18.(1)证明:连结OC.∵AC平分∠BAD,∴∠DAC=∠CAO.
∵OA=OC,∴∠CAO=∠OCA,∴∠DAC=∠OCA,
∴AD∥OC.
∵AD⊥DC,∴CO⊥DC.
∵OC为⊙O的半径,∴CD是⊙O的切线.
(2)解:∵E是BC的中点,且OA=OB,
∴OE是△ABC的中位线,∴AC=2OE.
∵OE=3,
∴AC=6.
∵AB是⊙O的直径,
∴∠ACB=90°=∠ADC,
又∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴=,即=,
∴AD=.
19.解:(1)连结A11O,A7O.
由题意易得∠A7OA11=120°,直径的长为12,
∴劣弧A7A11的长==4π,
∵4π>12,∴劣弧A7A11的长度比直径长.
(2)PA1⊥A7A11.理由:连结OA1.
由题易知点A1,O,A7三点共线,
即A1A7是⊙O的直径,∴∠A7A11A1=90°,∴PA1⊥A7A11.
(3)∵PA7是⊙O的切线,∴PA7⊥A1A7,∴∠PA7A1=90°,
由题意易得∠PA1A7=60°,A1A7=12,
∴PA7=A1A7·tan 60°=12.
20.(1)证明:如图,连结OP,设BO与⊙O的另一个交点为C.
∵AP与⊙O相切于点P,
∴∠APO=90°,∴∠PAO+∠AOP=90°.
∵MO⊥CN,∴∠AOP+∠POC=90°,
∴∠PAO=∠POC.
∵∠POC=2∠PBO,∴∠PAO=2∠PBO.
(第20题)
(2)解:如图,连结PC,过点P作PD⊥OC于点D,则∠PDO=90°.
在Rt△AOP中,AO==.
由(1)可知∠POC=∠PAO,
∴Rt△POD∽Rt△OAP,
∴==,即==,
解得PD=3,OD=4,
∴CD=OC-OD=1.
在Rt△PDC中,PC==.
∵CB为⊙O的直径,
∴∠BPC=90°,
∴BP===3,
故BP的长为3.
一、选择题(每题3分,共24分)
1.⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5 B.6 C.7 D.8
2.如图,在⊙O中,=,∠1=45°,则∠2的度数为( )
A.60° B.30°
C.45° D.40°
(第2题) (第3题)
3.如图,PA,PB分别切⊙O于A,B两点,如果∠P=60°,PA=2,那么△PAB的周长为( )
A.2 B.6 C.7 D.4
4.已知圆锥的母线长为6 cm,底面圆的半径为3 cm,则此圆锥侧面展开图(扇形)的圆心角是( )
A.30° B.60°
C.90° D.180°
5.如图,已知⊙O中,∠AOB=100°,则∠ACB的度数是( )
A.50° B.100°
C.120° D.130°
(第5题) (第6题)
6.如图,△ABC是⊙O的内接三角形,AB=2 ,∠ACB=60°,连结OA,OB,则的长是( )
A. B. C.π D.
7.如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=2OE,则∠BCD的度数为( )
A.15° B.22.5° C.30° D.45°
(第7题) (第8题)
8.如图,等腰三角形ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AB=AC=5,BC=6,则DE的长是( )
A. B. C. D.
二、填空题(每题3分,共18分)
9.已知⊙O的半径是3 cm,点O到直线l的距离为4 cm,则⊙O与直线l的位置关系是__________.
10.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是________.
(第10题) (第11题)
11.如图,AB为⊙O的直径,∠ABC=36°,当∠BCD=______°时,CD为⊙O的切线.
12.如图,等边三角形ABC内接于半径为1的⊙O,则图中阴影部分的面积是________.
(第12题) (第13题)
13.如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是________.
14.如图,在平面直角坐标系中,点A(-6,8),B(-6,0),以A为圆心,4为半径作⊙A,点P为⊙A上一动点,M为OP的中点,连接BM,设BM的最大值为m,最小值为n,则m-n的值为________.
(第14题)
三、解答题(15题8分,16~20题每题10分,共58分)
15.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连结AD,BC,求证:
(1)=;
(2)AE=CE.
(第15题)
16.如图,以正六边形ABCDEF的边AB为边,在其内部作正方形ABMN,连结MC.求∠BCM的大小.
(第16题)
17.如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.
(1)若∠D=70°,求∠CAD的度数;
(2)若AC=8,DE=2,求AB的长.
(第17题)
18.如图,在半径为5的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,E是BC的中点,OE=3.
(1)求证:CD是⊙O的切线;
(2)求AD的长.
(第18题)
19.如图,⊙O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作⊙O的切线交A1A11的延长线于点P.
(1)通过计算比较直径和劣弧A7A11的长度哪个更长;
(2)连结A7A11,则A7A11和PA1有什么特殊的位置关系?请简要说明理由;
(3)求PA7的长.
(第19题)
20.在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连结一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.小明受此启发设计了一个“双连杆机构”,设计图如图①,两个固定长度的“连杆”AP,BP的连结点P在⊙O上,当点P在⊙O上转动时,带动点A,B分别在射线OM,ON上滑动,OM⊥ON.当AP与⊙O相切时,点B恰好落在⊙O上,如图②.
请仅就图②的情形解答下列问题.
(1)求证:∠PAO=2∠PBO;
(2)若⊙O的半径为5,AP=,求BP的长.
(第20题)
答案
一、1.A 2.C 3.B 4.D 5.D
6.D 点拨:过点O作OD⊥AB于点D,
则AD=DB=AB=,∠AOD=∠AOB,
由圆周角定理,得∠AOB=2∠ACB=120°,
∴∠AOD=60°,∴OA===2,
∴的长为=.
7.B
8.D 点拨:连结OA,OE,OB,OD,OB交DE于点H,如图.
(第8题)
∵等腰三角形ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,∴AO平分∠BAC,OE⊥BC,OD⊥AB,BE=BD.∵AB=AC,∴AO⊥BC,∴点A,O,E共线,即AE⊥BC,
∴BE=CE=3.
在Rt△ABE中,AE===4.
∵BD=BE=3,∴AD=2.
设⊙O的半径为r,则OD=OE=r,AO=4-r,
在Rt△AOD中,r2+22=(4-r)2,解得r=.
在Rt△BOE中,OB==.
∵BD=BE,OD=OE,∴OB垂直平分DE,∴DH=EH.
易得HE·OB=OE·BE,
∴HE===,
∴DE=2EH=.故选D.
二、9.相离 10.6 11.54 12.π-
13.(-,1) 点拨:∵四边形ABOC为圆的内接四边形,
∴∠ABO+∠ACO=180°.∵∠ACO=120°,
∴∠ABO=180°-120°=60°.
∵∠AOB=90°,∴AB为⊙D的直径,
∴D为AB的中点.
在Rt△ABO中,∵∠ABO=60°,
∴OB=AB=2,OA=AB·sin 60°=2 ,
∴A(-2 ,0),B(0,2),
∴点D的坐标为(-,1).
14.4
三、15.证明:(1)∵AB=CD,∴=,
∴+=+,∴=.
(2)∵=,∴AD=BC.
∵∠ADE=∠CBE,∠AED=∠CEB,
∴△ADE≌△CBE,∴AE=EC.
16.解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90°,AB=BM.
∴∠MBC=120°-90°=30°,BM=BC.
∴∠BCM=∠BMC.∴∠BCM=×(180°-30°)=75°.
17.解:(1)∵OA=OD,∠D=70°,∴∠OAD=∠D=70°,
∴∠AOD=180°-∠OAD-∠D=40°.
∵AB是半圆O的直径,∴∠C=90°.
∵OD∥BC,∴∠AEO=∠C=90°,即OD⊥AC.
∴=,∴∠CAD=∠AOD=20°.
(2)由(1)可知OD⊥AC,
∴AE=AC=×8=4.
设OA=x,则OE=OD-DE=x-2.
在Rt△OAE中,OE2+AE2=OA2,
即(x-2)2+42=x2,解得x=5.
∴AB=2OA=10.
18.(1)证明:连结OC.∵AC平分∠BAD,∴∠DAC=∠CAO.
∵OA=OC,∴∠CAO=∠OCA,∴∠DAC=∠OCA,
∴AD∥OC.
∵AD⊥DC,∴CO⊥DC.
∵OC为⊙O的半径,∴CD是⊙O的切线.
(2)解:∵E是BC的中点,且OA=OB,
∴OE是△ABC的中位线,∴AC=2OE.
∵OE=3,
∴AC=6.
∵AB是⊙O的直径,
∴∠ACB=90°=∠ADC,
又∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴=,即=,
∴AD=.
19.解:(1)连结A11O,A7O.
由题意易得∠A7OA11=120°,直径的长为12,
∴劣弧A7A11的长==4π,
∵4π>12,∴劣弧A7A11的长度比直径长.
(2)PA1⊥A7A11.理由:连结OA1.
由题易知点A1,O,A7三点共线,
即A1A7是⊙O的直径,∴∠A7A11A1=90°,∴PA1⊥A7A11.
(3)∵PA7是⊙O的切线,∴PA7⊥A1A7,∴∠PA7A1=90°,
由题意易得∠PA1A7=60°,A1A7=12,
∴PA7=A1A7·tan 60°=12.
20.(1)证明:如图,连结OP,设BO与⊙O的另一个交点为C.
∵AP与⊙O相切于点P,
∴∠APO=90°,∴∠PAO+∠AOP=90°.
∵MO⊥CN,∴∠AOP+∠POC=90°,
∴∠PAO=∠POC.
∵∠POC=2∠PBO,∴∠PAO=2∠PBO.
(第20题)
(2)解:如图,连结PC,过点P作PD⊥OC于点D,则∠PDO=90°.
在Rt△AOP中,AO==.
由(1)可知∠POC=∠PAO,
∴Rt△POD∽Rt△OAP,
∴==,即==,
解得PD=3,OD=4,
∴CD=OC-OD=1.
在Rt△PDC中,PC==.
∵CB为⊙O的直径,
∴∠BPC=90°,
∴BP===3,
故BP的长为3.
