反比例函数 北师大版[上学期]

反比例函数
一. 本周教学内容：
函数是在探索具体问题中数量关系和变化规律的基础上抽象出的重要数学概念，是研究现实世界变化规律的重要数学模型。我们曾在七年级下册和八年级上册学习过“变量之间的关系”和“一次函数”等内容，对函数已经有了初步的认识，在此基础上讨论反比例函数及其性质可以进一步领悟函数的概念并积累研究函数性质的方法及用函数观点处理实际问题的经验，为后继学习（如二次函数）产生积极影响。
本章通过对具体情境的分析，概括出反比例函数的表达形式，明确反比例函数的概念，通过例题和现实实例可以丰富对反比例函数的表达形式，理解反比例函数的意义。结合实例经历列表，描点连线等活动，理解函数的三种表示方法，逐步明确研究函数的一般要求。反比例函数的图象具体展现了反比例函数的整体直观形象，为学生探索反比例函数的性质提供了思维活动的空间。通过对反比例函数（k>0和k<0）图象的全面观察和比较，发现函数自身的规律，进行语言表达，在相互交流中发展从图象中获取信息的能力，同时可以使我们更牢固地掌握由自己发现的反比例函数的主要性质。
本章最后讨论了反比例函数的某些应用，包括在实际中的应用和在数学内部的应用。在这些数学活动中，教科书注意用函数观点来处理问题或对问题的解决用函数做出某种解释，用以加深对函数的认识，并突出知识之间的内在联系。
本章中直观、操作、观察、概括和交流仍是重要活动形式，通过这些活动。我们要达到以下几点①对函数的三种表示方法进行整合，逐步形成对函数概念的整体性认识；②逐步提高对函数图象中获得信息的能力，提高感知水平；③逐步形成函数观点处理问题的意识，体验数形结合的思想方法。
二. 学习目标：
1. 经历在具体问题中探索数量关系和变化规律的过程，抽象出反比例函数的概念，并结合具体情境领会反比例函数作为一种数学模型的意义。
2. 能画出反比例函数的图象，根据图象和解析表达式探索并理解反比例函数的主要性质。
3. 逐步提高观察和归纳分析能力，体验数形结合的数学思想方法。
4. 能依据已知条件确定反比例函数，领悟用函数观点解决某些实际问题的基本思路。
三. 重、难点分析及应注意的问题：
①注重数学概念的形成过程和对概念意义的理解。
在反比例函数概念形成的过程中，应充分利用我们已有的生活经验和背景知识，创设丰富的现实情况，关注问题中变量的相依关系及变化规律，并逐步加深理解。
②创设学生自主探索与合作交流的环境
函数的性质蕴涵于概念之中，对反比例函数性质的探索是对其概念内在规定性的认识。学习时，要在了解函数三种表示方法的基础上，通过观察，分析函数的图象，自主地对反比例函数的主要性质作出直观描述。
③经历数学知识的应用过程，关注对问题的分析过程。
用函数观点处理实际问题的关键在于分析实际情境，建立函数模型，并进一步提出明确的数学问题。学习时应注意分析的过程即将实际问题置于已有知识背景之中，用数学知识重新解释，逐步学会用数学的眼光考察实际问题。同时，在解决问题的过程中，要充分利用函数的图象，渗透数形结合的思想。此外，解决问题时，还要体会知识之间的联系以及知识的综合运用。
【典型例题】
例1.
分析：
1. 作图的一般步骤：列表、描点、连线。
2. 观察x可以取哪些值，x≠0，不妨从0的左右对称的取。
列表：
x －6 －5 －4 －3 －2 －1 1 2 3 4 5 6
－1 － － －2 －3 －6 6 3 2 1

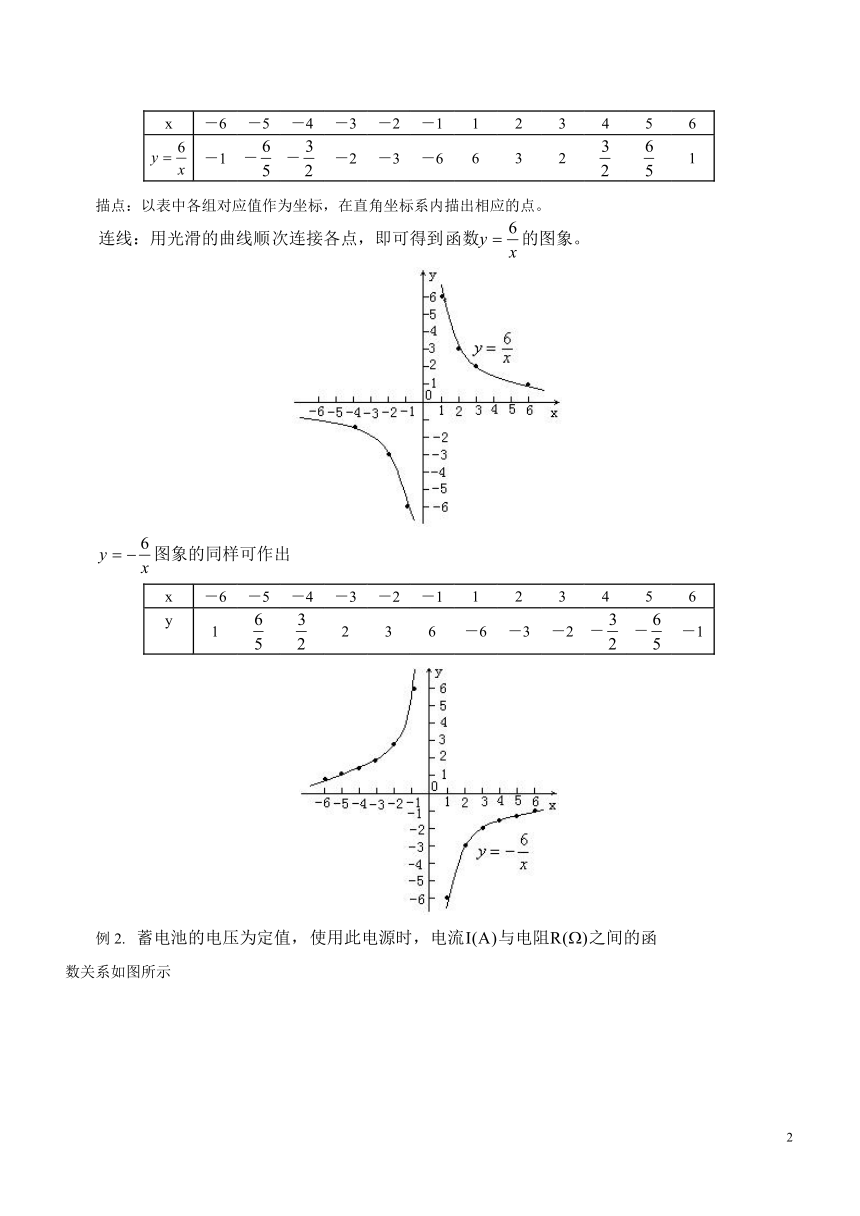
描点：以表中各组对应值作为坐标，在直角坐标系内描出相应的点。
x －6 －5 －4 －3 －2 －1 1 2 3 4 5 6
y 1 2 3 6 －6 －3 －2 － － －1

例2.
数关系如图所示
（1）蓄电池的电压是多少？你能写出这一函数的表达式吗？
（2）完成下表，并回答问题：如果以此蓄电池为电源的用电器限制电流不超过10A，那么用电器的可变电阻应控制在什么范围内？
3 4 5 6 7 8 9 10
I/A 4

图形所提供的信息包括：①直观上看，I与R之间可能是反比例函数，根据物理学中的相关知识IR=U（U为定值）得到确认。②由图象上点A的坐标可知，当用电器电阻为
（2）
3 4 5 6 7 8 9 10
I/A 12 9 7.2 6 5.1 4.5 4 3.6

由此表可知，当电阻逐步增大时，电流越变越小。
R≥3.6。
例3.
标是1，求它们两个交点的坐标。
分析：①这两个函数的交点的坐标既满足正比例函数的关系式，又满足反比例函数的关系式，不妨设这个交点为（1，y），并将它分别代入这个关系式中，因为y是相同的就会得到关于a的一元一次方程，将a解出。
②a已知后，两个函数也已确定下来了，将它们联立起来，得到一个方程组，将其解出，即为两个交点坐标。
解：①设这个交点为（1，y），将其分别代入两个关系式中
解得，x=±1。
将x=±1，代入y=3x中，得y=±3。
∴这两个交点为（1，3）和（－1，－3）。
【模拟试题】
一、填空题（每小题4分，共36分）
1. 已知y与x成反比例，且当x时，y=5，则y与x的函数关系式为__________。
2. 矩形的面积为5，那么该矩形的一边x与另一边y的函数关系式为y=__________，该函数图像位于第__________象限，y随x的增大而__________（填“增大”或“减小”）。
3. 已知反比例函数的图像经过点（－1，6），那么函数的图像经过点（－1，__________）。
4. 已知，与x成正比例，与x成反比例，当x=1时，y=2；当x=5时，y=－14，那么当x=－2时y=__________。
5. 反比例函数的图像在所在的象限内，y随x的增大而增大，那么m的取值范围是__________。
6. 反比例函数的图像在各自的象限，y随x的增大而减小，则m=__________。
7. 一次函数和反比例函数的图像有两个交点，如果一个交点的横坐标为3，那么b=__________。
8. 当电源电压为220V时，某一电阻R与通过的电流强度I的函数关系式为R=__________，当电阻为1100（）时，电流强度为__________（A）
9. 点A（x1，y1）、B（x2，y2）在双曲线上，且当x1>x2>0时，有y1>y2，则k的取值范围是__________。
二、选择题（每小题4分，共28分）
1. 下列不是表示反比例函数关系的式子有（ ）。
A. B. C. D.
2. 下列各变量之间的关系属于反比例函数关系的有（ ）。
①当路程一定时，汽车行驶的平均速度v与行驶时间t之间的关系
②当电压一定时，电路中的电阻R与通过的电流强度I之间的函数关系
③当矩形面积一定时，矩形的两边a与b之间的函数关系
④当受力一定时，物体所受到的压强P与受力面积S之间的函数关系
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
3. 已知点M（a1，b1），N（a2，b2）都在函数的图像上，若a1>a2>0，那么，关于b1，b2的大小关系正确的是（ ）。
A. b1>b2>0 B. b1b1>0 D. b24. 已知点A（a，b）在的图象上，那么此图象必过（ ）。
A. （） B. C. D. （0，0）
5. 函数y=k(x－2)与函数（k≠0）在同一坐标系的图象大致是（ ）。
6. 反比例函数与一次函数y=－ax的图像在同一坐标系下交点的个数是（ ）。
A. 1个 B. 2个 C. 没有交点 D. a的值不确定，交点的个数也不能确定
7. y与z成正比例函数关系；z与x成反比例函数关系，那么y与x的函数关系是（ ）。
A. 正比例函数关系 B. 反比例函数关系
C. 既不是正比例函数也不是反比例函数关系 D. 无法确定
三. 解答题（共36分）
1. 已知△ABC，，若△ABC的面积S=4，写出边长a与边a上的高h的函数关系式，并画出这个函数的图像的草图。
2. 小美拿100元钱去买巧克力，预计巧克力每千克x元，可购得y1千克，到了商场，只有另一种品牌的巧克力，每千克比预计贵了5元，只能购得y2千克。
（1）写出y1与x的函数关系式。
（2）写出y2与x的函数关系式。
（3）在同一坐标系下画出上述两支函数图像。
（4）观察图像比较y1与y2的差与x的关系。
3. 如图所示为某人对地面的压强与这个人和地面接触面积的函数关系图像。
（1）通过图像你能确定这个人的体重么？
（2）如果此人穿40码的鞋，若每只鞋与地面的接触面积大约是300cm2，那么此人双脚站立时对地面的压强有多大？
（3）若某一沼泽地能承受的压强为300牛/米2，那么此人应站立在面积至少多大的木板上才不至于下陷（木板的重量忽略不记）
4. （1）一电源E给不同电阻值的电阻供电，测量通过各电阻的电流，结果如下
5 10 15 20 25 30 ……
IA 0.6 0.3 0.2 0.15 0.12 0.1 ……
（2）一电组R加上不同的电压，测的相应的电流如图所示：
U 2.4 4.8 7.2 9.6 12 ……
I 0.2 0.4 0.6 0.8 1 ……
要求：
（1）根据表（1）的数据，求出I关于R的函数关系式，画出图像，并确定这一电源E的电压。
（2）根据表（2）的数据，求出I关于U的函数关系式，画出图像，并确定这一电阻R的阻值。
（3）当电源E给电阻R供电时，电流是多少？
【试题答案】
一、1. 2. ，一、减小 3. （－1，3） 4. 5. m>1
6. 7. 4 8. ，0.2 9. k<0
二、1. B 2. D 3. C 4. C 5. D 6. C 7. B
三、1. ，图像略
2. （1），（2），（3）略，（4）随x的增大，y1与y2的差越来越小。
3. （1） 体重约是60kg。
（2）P=104牛/米2
（3）2m2
4. （1）图像略。电压3V
（2）图像略。电阻12
（3）
PAGE
3