安徽省合肥市重点中学2022-2023学年高二上学期9月入学考试数学试题(含答案)
文档属性
| 名称 | 安徽省合肥市重点中学2022-2023学年高二上学期9月入学考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 627.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 00:00:00 | ||
图片预览

文档简介
合肥市重点中学2022-2023学年高二上学期9月入学考试
数学试题
一、单项选择题(本大题共8小题,每小题3分,共24分)
1.若, 则“”是 “”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.按从小到大顺序排列的 9 个数据: 10,16,25,33,39,43, m, 65,70, 若这组数据的第一四分位数与第三四分位数的和是73 , 则等于( )
A.40 B.45 C.48 D.62
3.设是两条不同的直线,是两个不同的平面, 则下列命题正确的是( )
A.若, 则 B.若, 则
C.若, 则 D.若, 则
4.已知长方体的表面积是, 过同一个顶点的三条棱长之和是, 则它的体对角线长是( )
A. B. C. D.
5.三棱锥中,是棱的中点, 若, 则值为( )
A.0 B.-1 C.1 D.
6.锐角的三个内角所对的边分别是, 某数学兴趣小组探究该三角形时, 提出以下四个论断: 甲:; 乙:; 丙:; 丁:.若上述四个论断中有且只有一个是正确的, 则正确的是( )
A.甲 B.乙 C.丙 D.丁
7.如图, 在平面四边形中,, 则向量在向量 上的投影向量为( )
A. B. C. D.
8.已知定义域为的函数的图像是一条连续不断的曲线, 且满足.若, 当时, 总有, 则满足的实数 的取值范围为( )
A. B. C. D.
二、多项选择题(本大题共 4 小题, 每小题 4 分, 共 16 分)
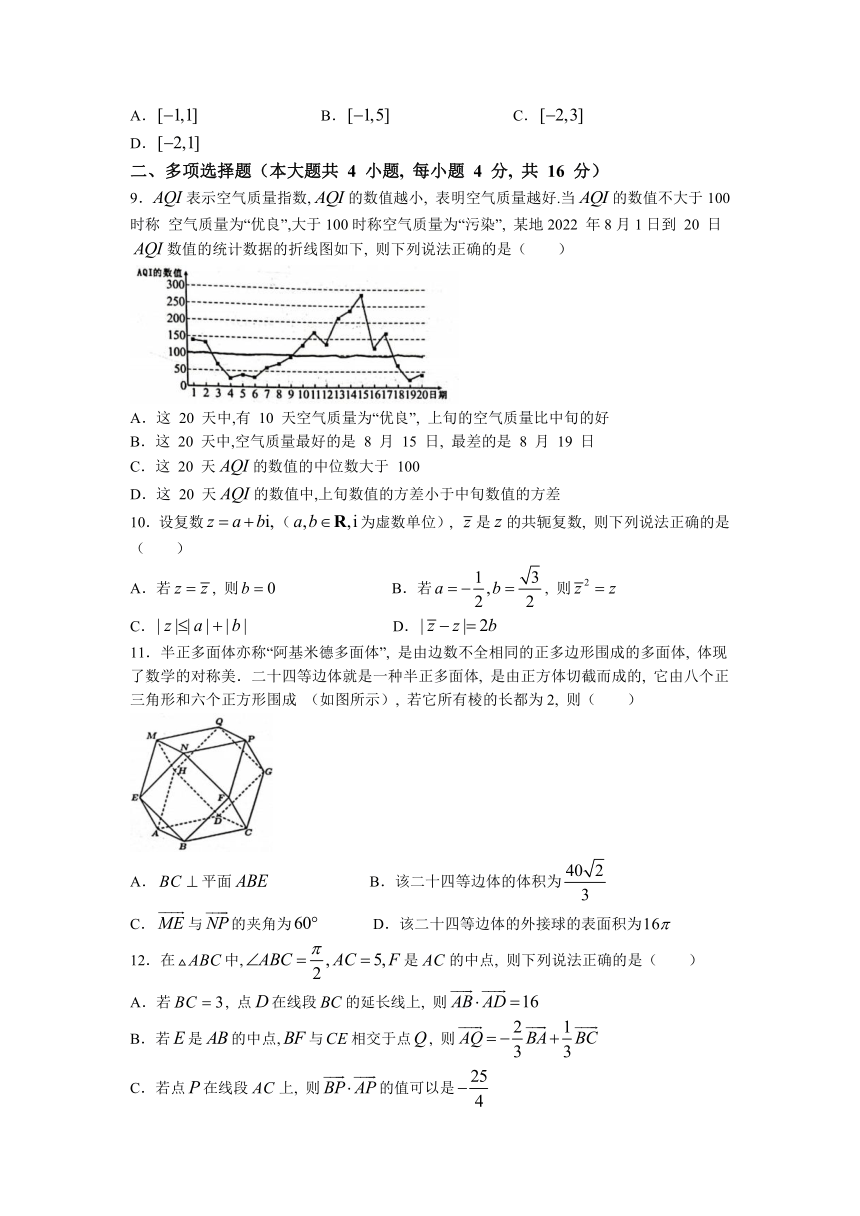
9.表示空气质量指数,的数值越小, 表明空气质量越好.当的数值不大于100 时称 空气质量为“优良”,大于100时称空气质量为“污染”, 某地2022 年8月1日到 20 日数值的统计数据的折线图如下, 则下列说法正确的是( )
A.这 20 天中,有 10 天空气质量为“优良”, 上旬的空气质量比中旬的好
B.这 20 天中,空气质量最好的是 8 月 15 日, 最差的是 8 月 19 日
C.这 20 天的数值的中位数大于 100
D.这 20 天的数值中,上旬数值的方差小于中旬数值的方差
10.设复数(为虚数单位), 是的共轭复数, 则下列说法正确的是( )
A.若, 则 B.若, 则
C. D.
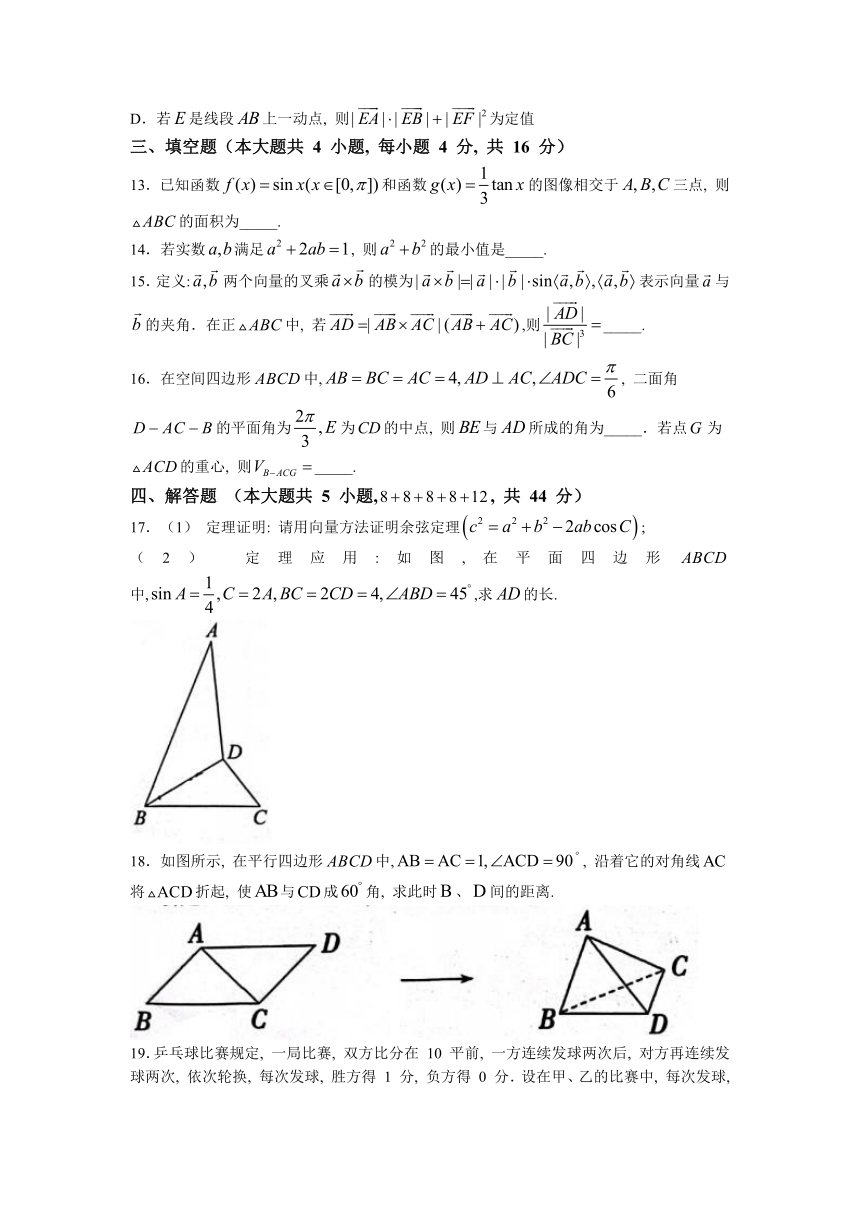
11.半正多面体亦称“阿基米德多面体”, 是由边数不全相同的正多边形围成的多面体, 体现了数学的对称美.二十四等边体就是一种半正多面体, 是由正方体切截而成的, 它由八个正三角形和六个正方形围成 (如图所示), 若它所有棱的长都为2, 则( )
A.平面 B.该二十四等边体的体积为
C.与的夹角为 D.该二十四等边体的外接球的表面积为
12.在中,是的中点, 则下列说法正确的是( )
A.若, 点在线段的延长线上, 则
B.若是的中点,与相交于点, 则
C.若点在线段上, 则的值可以是
D.若是线段上一动点, 则为定值
三、填空题(本大题共 4 小题, 每小题 4 分, 共 16 分)
13.已知函数和函数的图像相交于三点, 则的面积为_____.
14.若实数满足, 则的最小值是_____.
15.定义:两个向量的叉乘的模为表示向量与的夹角.在正中, 若,则_____.
16.在空间四边形中,, 二面角的平面角为为的中点, 则与所成的角为_____.若点为的重心, 则_____.
四、解答题 (本大题共 5 小题,, 共 44 分)
17.(1) 定理证明: 请用向量方法证明余弦定理;
(2) 定理应用:如图,在平面四边形中,,求的长.
18.如图所示, 在平行四边形中,, 沿着它的对角线将折起, 使与成角, 求此时、间的距离.
19.乒乓球比赛规定, 一局比赛, 双方比分在 10 平前, 一方连续发球两次后, 对方再连续发球两次, 依次轮换, 每次发球, 胜方得 1 分, 负方得 0 分.设在甲、乙的比赛中, 每次发球, 发球方得 1 分的概率为0.6, 各次发球的胜负结果相互独立.甲、乙的一局比赛中, 甲先发球.
(1)求开始第四次发球时, 甲、乙的比分为 1 比 2 的概率;
(2)求开始第五次发球时, 甲得分始终领先的概率.
20.如图, 在四棱锥中, 平面平面是等边三角形, 已知 .
(1) 设是上的一点, 求证: 平面平面;
(2) 求四棱锥的体积.
21.定义:若对定义域内任意,都有(为正常数),则称函数为“距”增函数.
(1) 若, 试判断是否为 “ 1 距” 增函数, 并说明理由;
(2)若是“距”增函数, 求的取值范围;
(3)若, 其中,且为“ 2 距”增函数, 求的最小值.
合肥市重点中学2022-2023学年高二上学期9月入学考试
数学参考答案
一、单项选择题(本大题共8小题,每小题3分,共24分)
1 2 3 4 5 6 7 8
A C C D A C B A
二、多项选择题(本大题共4小题,每小题4分,共16分)
11 12 13 14
ACD ABC BD ABD
三、填空题(本大题共4小题,每小题4分,共16分)
13. 14. 15. 16.;
四、解答题(本大题共5小题,8+8+8+8+12,共44分)
17.解:(1)证明:设,
由三角形法则有,所以,
所以,
即.
(2)因为,所以,
因为,由余弦定理得,
所以,由正弦定理,得.
18.解:在平行四边形中,因为,所以,同理可得,
在空间四边形中,因为与成角,所以或,
又,
所以
所以当时,,此时B,D两点间的距离为2;
当时,,此时B,D两点间的距离为.
19.解:(1)记“第1次和第2次这两次发球,甲共得i分,”为事件;
“第3次和第4次这两次发球,甲共得i分,”为事件;
“第3次发球,甲得1分”为事件A;
“开始第4次发球时,甲、乙的比分为1比2”为事件B.
,
,
;
(2)记“开始第5次发球时,甲得分领先”为事件C,
,
,
.
20.解:(1)取的中点E,连接,因为是等边三角形,所以.
因为平面平面,平面平面平面,所以平面,
又平面,所以,在中,,
所以,由勾股定理的逆定理知,,又,
所以平面,因为平面,所以平面平面.
(2)过点D作交于点F,
在中,,所以,
因为,所以梯形的面积是,因为是等边三角形,且边长为4,所以,因为平面,所以是四棱锥的高,
所以四棱锥的体积.
21.解析:(1)任意,
因为,所以,所以,即是“1距”增函数;
(2),因为是“a距”增函数,所以恒成立,因为,所以在R上恒成立,
所以,解得;
(3)因为,且为“2距”增函数,
所以恒成立,即时,恒成立,
所以,当时,,即恒成立,所以,得;
当时,,得恒成立,
所以,得,
综上可得,,
又,因为,所以,
当时,若取最小值为0;
当时,若取最小值,
因为在R上是单调递增函数,
所以当的最小值为1;当时,的最小值为,
即.
数学试题
一、单项选择题(本大题共8小题,每小题3分,共24分)
1.若, 则“”是 “”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.按从小到大顺序排列的 9 个数据: 10,16,25,33,39,43, m, 65,70, 若这组数据的第一四分位数与第三四分位数的和是73 , 则等于( )
A.40 B.45 C.48 D.62
3.设是两条不同的直线,是两个不同的平面, 则下列命题正确的是( )
A.若, 则 B.若, 则
C.若, 则 D.若, 则
4.已知长方体的表面积是, 过同一个顶点的三条棱长之和是, 则它的体对角线长是( )
A. B. C. D.
5.三棱锥中,是棱的中点, 若, 则值为( )
A.0 B.-1 C.1 D.
6.锐角的三个内角所对的边分别是, 某数学兴趣小组探究该三角形时, 提出以下四个论断: 甲:; 乙:; 丙:; 丁:.若上述四个论断中有且只有一个是正确的, 则正确的是( )
A.甲 B.乙 C.丙 D.丁
7.如图, 在平面四边形中,, 则向量在向量 上的投影向量为( )
A. B. C. D.
8.已知定义域为的函数的图像是一条连续不断的曲线, 且满足.若, 当时, 总有, 则满足的实数 的取值范围为( )
A. B. C. D.
二、多项选择题(本大题共 4 小题, 每小题 4 分, 共 16 分)
9.表示空气质量指数,的数值越小, 表明空气质量越好.当的数值不大于100 时称 空气质量为“优良”,大于100时称空气质量为“污染”, 某地2022 年8月1日到 20 日数值的统计数据的折线图如下, 则下列说法正确的是( )
A.这 20 天中,有 10 天空气质量为“优良”, 上旬的空气质量比中旬的好
B.这 20 天中,空气质量最好的是 8 月 15 日, 最差的是 8 月 19 日
C.这 20 天的数值的中位数大于 100
D.这 20 天的数值中,上旬数值的方差小于中旬数值的方差
10.设复数(为虚数单位), 是的共轭复数, 则下列说法正确的是( )
A.若, 则 B.若, 则
C. D.
11.半正多面体亦称“阿基米德多面体”, 是由边数不全相同的正多边形围成的多面体, 体现了数学的对称美.二十四等边体就是一种半正多面体, 是由正方体切截而成的, 它由八个正三角形和六个正方形围成 (如图所示), 若它所有棱的长都为2, 则( )
A.平面 B.该二十四等边体的体积为
C.与的夹角为 D.该二十四等边体的外接球的表面积为
12.在中,是的中点, 则下列说法正确的是( )
A.若, 点在线段的延长线上, 则
B.若是的中点,与相交于点, 则
C.若点在线段上, 则的值可以是
D.若是线段上一动点, 则为定值
三、填空题(本大题共 4 小题, 每小题 4 分, 共 16 分)
13.已知函数和函数的图像相交于三点, 则的面积为_____.
14.若实数满足, 则的最小值是_____.
15.定义:两个向量的叉乘的模为表示向量与的夹角.在正中, 若,则_____.
16.在空间四边形中,, 二面角的平面角为为的中点, 则与所成的角为_____.若点为的重心, 则_____.
四、解答题 (本大题共 5 小题,, 共 44 分)
17.(1) 定理证明: 请用向量方法证明余弦定理;
(2) 定理应用:如图,在平面四边形中,,求的长.
18.如图所示, 在平行四边形中,, 沿着它的对角线将折起, 使与成角, 求此时、间的距离.
19.乒乓球比赛规定, 一局比赛, 双方比分在 10 平前, 一方连续发球两次后, 对方再连续发球两次, 依次轮换, 每次发球, 胜方得 1 分, 负方得 0 分.设在甲、乙的比赛中, 每次发球, 发球方得 1 分的概率为0.6, 各次发球的胜负结果相互独立.甲、乙的一局比赛中, 甲先发球.
(1)求开始第四次发球时, 甲、乙的比分为 1 比 2 的概率;
(2)求开始第五次发球时, 甲得分始终领先的概率.
20.如图, 在四棱锥中, 平面平面是等边三角形, 已知 .
(1) 设是上的一点, 求证: 平面平面;
(2) 求四棱锥的体积.
21.定义:若对定义域内任意,都有(为正常数),则称函数为“距”增函数.
(1) 若, 试判断是否为 “ 1 距” 增函数, 并说明理由;
(2)若是“距”增函数, 求的取值范围;
(3)若, 其中,且为“ 2 距”增函数, 求的最小值.
合肥市重点中学2022-2023学年高二上学期9月入学考试
数学参考答案
一、单项选择题(本大题共8小题,每小题3分,共24分)
1 2 3 4 5 6 7 8
A C C D A C B A
二、多项选择题(本大题共4小题,每小题4分,共16分)
11 12 13 14
ACD ABC BD ABD
三、填空题(本大题共4小题,每小题4分,共16分)
13. 14. 15. 16.;
四、解答题(本大题共5小题,8+8+8+8+12,共44分)
17.解:(1)证明:设,
由三角形法则有,所以,
所以,
即.
(2)因为,所以,
因为,由余弦定理得,
所以,由正弦定理,得.
18.解:在平行四边形中,因为,所以,同理可得,
在空间四边形中,因为与成角,所以或,
又,
所以
所以当时,,此时B,D两点间的距离为2;
当时,,此时B,D两点间的距离为.
19.解:(1)记“第1次和第2次这两次发球,甲共得i分,”为事件;
“第3次和第4次这两次发球,甲共得i分,”为事件;
“第3次发球,甲得1分”为事件A;
“开始第4次发球时,甲、乙的比分为1比2”为事件B.
,
,
;
(2)记“开始第5次发球时,甲得分领先”为事件C,
,
,
.
20.解:(1)取的中点E,连接,因为是等边三角形,所以.
因为平面平面,平面平面平面,所以平面,
又平面,所以,在中,,
所以,由勾股定理的逆定理知,,又,
所以平面,因为平面,所以平面平面.
(2)过点D作交于点F,
在中,,所以,
因为,所以梯形的面积是,因为是等边三角形,且边长为4,所以,因为平面,所以是四棱锥的高,
所以四棱锥的体积.
21.解析:(1)任意,
因为,所以,所以,即是“1距”增函数;
(2),因为是“a距”增函数,所以恒成立,因为,所以在R上恒成立,
所以,解得;
(3)因为,且为“2距”增函数,
所以恒成立,即时,恒成立,
所以,当时,,即恒成立,所以,得;
当时,,得恒成立,
所以,得,
综上可得,,
又,因为,所以,
当时,若取最小值为0;
当时,若取最小值,
因为在R上是单调递增函数,
所以当的最小值为1;当时,的最小值为,
即.
同课章节目录
