2022-2023学年北师大版八年级 数学上册1.3 勾股定理的应用 课堂提升训练(含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级 数学上册1.3 勾股定理的应用 课堂提升训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 393.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 17:35:04 | ||
图片预览




文档简介
2022-2023学年度初中数学北师大版 八年级上册
课堂提升训练
第一章 勾股定理
3 勾股定理的应用
基础过关全练
知识点1 确定立体图形上的最短距离
1.如图,若圆柱的底面周长是50 cm,高是120 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.170 cm B.70 cm
C.145 cm D.130 cm
2.如图所示,正方体的棱长为1,一只蜘蛛从正方体的一个顶点A爬行到另一个顶点B,则蜘蛛爬行的最短距离的平方是( )
A.2 B.3 C.4 D.5
3.如图是一个底面为等边三角形的三棱镜,在三棱镜的侧面上,从顶点A到顶点A'镶有一圈金属丝,已知此三棱镜的高为5 cm,底面边长为4 cm,则这圈金属丝的长度至少为( )
A.8 cm B.13 cm C.12 cm D.15 cm
4.(教材P13变式题)如图,圆柱的底面直径BC= cm,高AB=8 cm,按如图所示的方式缠绕细线,则缠绕一周(不记接头)至少需要 cm长的细线.
5.(2022独家原创)长方体共顶点的三条棱长如图所示,三只蚂蚁同时从点A出发,同速沿长方体表面爬行去点M处觅食,蚂蚁甲、乙、丙的爬行路径分别为A→B→M、A→C→M、A→D→M,若三只蚂蚁都爬行自己的最短路径,通过计算说明哪只蚂蚁最先到达,哪只蚂蚁最后到达
知识点2 勾股定理的实际应用
6.(2022陕西西安铁一中学期中)如图所示,有一个由传感器A控制的灯,要装在门上方离地高4.5 m的墙上,任何东西只要移至该灯5 m及5 m以内时,灯就会自动发光.请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光 ( )
A.4米 B.3米 C.5米 D.7米
7.有诗曰:“平地秋千未起,踏板一尺离地.送行二岁与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉,良工高士好奇,算出索长有几.”(注:一步等于5尺,图示如图)
能力提升全练
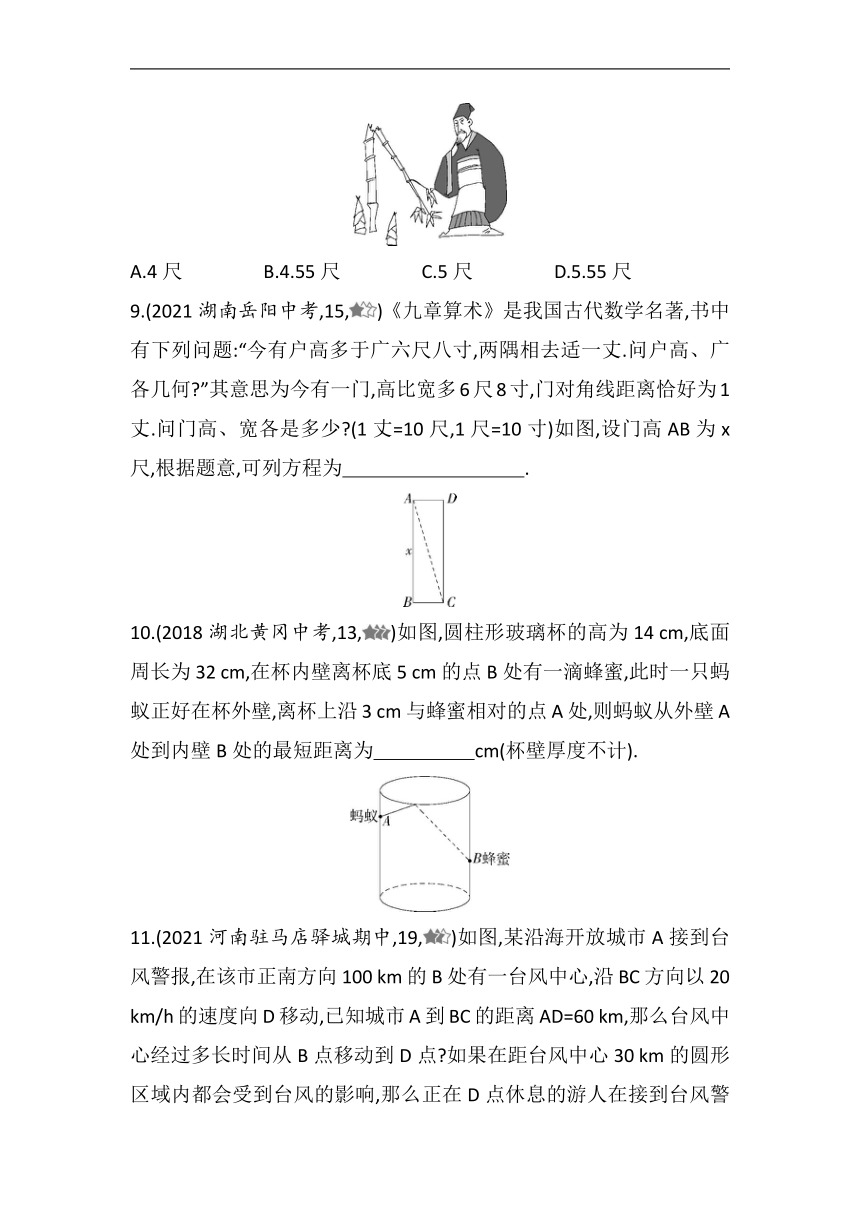
8.(2020四川巴中中考,8,)《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何 ”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子 ( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
9.(2021湖南岳阳中考,15,)《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何 ”其意思为今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少 (1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 .
10.(2018湖北黄冈中考,13,)如图,圆柱形玻璃杯的高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
11.(2021河南驻马店驿城期中,19,)如图,某沿海开放城市A接到台风警报,在该市正南方向100 km的B处有一台风中心,沿BC方向以20 km/h的速度向D移动,已知城市A到BC的距离AD=60 km,那么台风中心经过多长时间从B点移动到D点 如果在距台风中心30 km的圆形区域内都会受到台风的影响,那么正在D点休息的游人在接到台风警报后的几小时内撤离才可脱离危险
素养探究全练
12.[直观想象](2022江苏连云港期中)如图,在Rt△ABC中,∠ACB=
90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动时间为t(s).
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
13.[直观想象]为筹备迎新晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图.已知圆筒的高为108 cm,其横截面周长为36 cm,如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸
答案全解全析
基础过关全练
1.D 如图,圆柱侧面展开图为长方形,连接AB,根据勾股定理得AB2=502+1202=16 900=1302,所以AB=130 cm,故选D.
2.D 将正方体的前面、上面展开放在同一平面上,连接AB,如图所示,爬行的最短路径为线段AB.由勾股定理得,AB2=(1+1)2+12=5,故选D.
3.B 如图为三棱柱的侧面展开图,则AB=5 cm,
A'B=4×3=12 cm,由勾股定理得AA'2=A'B2+AB2=122+52=169=132,
所以AA'=13 cm,故选B.
4.20
解析 如图为圆柱的侧面展开图,连接AC、CD,由已知得 AB=8 cm,BC=××π=6 cm,在Rt△ABC中,AC2=AB2+BC2=82+62=102,所以AC=10 cm,所以至少需要10×2=20 cm长的细线.
5.解析 图1、图2、图3中AM分别为甲、乙、丙三只蚂蚁所走的最短路径.
图1 图2 图3
图1中AM2=82+92=145.
图2中AM2=52+122=169.
图3中AM2=132+42=185.
因为145<169<185,
所以蚂蚁甲最先到达,蚂蚁丙最后到达.
6.A 当人走到点D的位置,头顶C与点A的距离是5 m时,灯刚好自动发光,作CE⊥AB于E,由题意可知,BE=CD=1.5 m,AE=AB-BE=4.5-1.5=3 m,AC=5 m,
在Rt△ACE中,CE2=AC2-AE2=52-32=16,
∴CE=4 m.
故学生走到离墙4 m远时,灯刚好发光,
故选A.
7.解析 如图,设OA=x尺,根据题意,得OB=OA=x尺,BC=10尺,
OC=(x-4)尺,
在Rt△OCB中,CO2+CB2=OB2,
即(x-4)2+102=x2,
解得x=14.5,
所以索长为14.5尺.
能力提升全练
8.B 设竹子折断处离地面x尺,则斜边为(10-x)尺,
根据勾股定理得x2+32=(10-x)2,
解得x=4.55.
所以原处还有4.55尺高的竹子.
故选B.
9.(x-6.8)2+x2=102
解析 因为门高AB为x尺,所以门宽BC为(x-6.8)尺,依题意得BC2+AB2=AC2,∵AC=1丈=10尺,
∴(x-6.8)2+x2=102.故答案为(x-6.8)2+x2=102.
10.20
解析 如图,将杯子侧面展开,作A关于EF的对称点A',
连接A'B,作A'D⊥BE,交BE的延长线于D,则A'B的长即为最短距离,A'B2=A'D2+BD2=162+122=202,
所以 A'B=20 cm,故答案为20.
11.解析 在Rt△ABD中,根据勾股定理,得BD2=AB2-AD2=1002-602=6 400,∴BD=80 km,∵80÷20=4(h),
∴台风中心经过4小时从B点移动到D点.
如图,∵距台风中心30 km的圆形区域内都会受到台风的影响,∴游人要在台风中心到达E点之前撤离,
∵BE=BD-DE=80-30=50 km,=2.5(h),
∴游人在接到台风警报后2.5小时内撤离才可脱离危险.
素养探究全练
12.解析 (1)∵∠ACB=90°,∴BC2=AB2-AC2=102-62=64,∴BC=8(cm).
当△ABP为直角三角形时,可分为两种情况进行讨论:
①当∠APB=90°时,点P与点C重合,此时BP=BC=8 cm,∴t=8÷1=8.
②当∠BAP=90°时,BP=t cm,CP=(t-8)cm,
在Rt△ACP中,AP2=62+(t-8)2,在Rt△BAP中,AB2+AP2=BP2,
即102+[62+(t-8)2]=t2,解得t=.
综上所述,当△ABP为直角三角形时,t=8或.
(2)由(1)可知,BC=8 cm.
当△ABP为等腰三角形时,可分三种情况进行讨论:
①当AB=AP时,BP=2BC=16 cm,即t=16;
②当BP=BA=10 cm时,t=10;
③当PA=PB时,如图,设BP=PA=x cm,则PC=(8-x)cm,
在Rt△ACP中,由勾股定理得PC2+AC2=AP2,
∴(8-x)2+62=x2,解得x=,∴BP= cm.∴t=.
综上所述,当△ABP为等腰三角形时,t的值为16或10或.
13.解析 如图为该灯罩的展开图,在Rt△ABC中,
因为AC=36 cm,BC=108÷4=27(cm),
所以由勾股定理,得AB2=AC2+BC2=362+272=2 025=452,
所以AB=45 cm,
所以应裁剪45×4=180 cm的油纸.
课堂提升训练
第一章 勾股定理
3 勾股定理的应用
基础过关全练
知识点1 确定立体图形上的最短距离
1.如图,若圆柱的底面周长是50 cm,高是120 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.170 cm B.70 cm
C.145 cm D.130 cm
2.如图所示,正方体的棱长为1,一只蜘蛛从正方体的一个顶点A爬行到另一个顶点B,则蜘蛛爬行的最短距离的平方是( )
A.2 B.3 C.4 D.5
3.如图是一个底面为等边三角形的三棱镜,在三棱镜的侧面上,从顶点A到顶点A'镶有一圈金属丝,已知此三棱镜的高为5 cm,底面边长为4 cm,则这圈金属丝的长度至少为( )
A.8 cm B.13 cm C.12 cm D.15 cm
4.(教材P13变式题)如图,圆柱的底面直径BC= cm,高AB=8 cm,按如图所示的方式缠绕细线,则缠绕一周(不记接头)至少需要 cm长的细线.
5.(2022独家原创)长方体共顶点的三条棱长如图所示,三只蚂蚁同时从点A出发,同速沿长方体表面爬行去点M处觅食,蚂蚁甲、乙、丙的爬行路径分别为A→B→M、A→C→M、A→D→M,若三只蚂蚁都爬行自己的最短路径,通过计算说明哪只蚂蚁最先到达,哪只蚂蚁最后到达
知识点2 勾股定理的实际应用
6.(2022陕西西安铁一中学期中)如图所示,有一个由传感器A控制的灯,要装在门上方离地高4.5 m的墙上,任何东西只要移至该灯5 m及5 m以内时,灯就会自动发光.请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光 ( )
A.4米 B.3米 C.5米 D.7米
7.有诗曰:“平地秋千未起,踏板一尺离地.送行二岁与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉,良工高士好奇,算出索长有几.”(注:一步等于5尺,图示如图)
能力提升全练
8.(2020四川巴中中考,8,)《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何 ”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子 ( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
9.(2021湖南岳阳中考,15,)《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何 ”其意思为今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少 (1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 .
10.(2018湖北黄冈中考,13,)如图,圆柱形玻璃杯的高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
11.(2021河南驻马店驿城期中,19,)如图,某沿海开放城市A接到台风警报,在该市正南方向100 km的B处有一台风中心,沿BC方向以20 km/h的速度向D移动,已知城市A到BC的距离AD=60 km,那么台风中心经过多长时间从B点移动到D点 如果在距台风中心30 km的圆形区域内都会受到台风的影响,那么正在D点休息的游人在接到台风警报后的几小时内撤离才可脱离危险
素养探究全练
12.[直观想象](2022江苏连云港期中)如图,在Rt△ABC中,∠ACB=
90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动时间为t(s).
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
13.[直观想象]为筹备迎新晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图.已知圆筒的高为108 cm,其横截面周长为36 cm,如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸
答案全解全析
基础过关全练
1.D 如图,圆柱侧面展开图为长方形,连接AB,根据勾股定理得AB2=502+1202=16 900=1302,所以AB=130 cm,故选D.
2.D 将正方体的前面、上面展开放在同一平面上,连接AB,如图所示,爬行的最短路径为线段AB.由勾股定理得,AB2=(1+1)2+12=5,故选D.
3.B 如图为三棱柱的侧面展开图,则AB=5 cm,
A'B=4×3=12 cm,由勾股定理得AA'2=A'B2+AB2=122+52=169=132,
所以AA'=13 cm,故选B.
4.20
解析 如图为圆柱的侧面展开图,连接AC、CD,由已知得 AB=8 cm,BC=××π=6 cm,在Rt△ABC中,AC2=AB2+BC2=82+62=102,所以AC=10 cm,所以至少需要10×2=20 cm长的细线.
5.解析 图1、图2、图3中AM分别为甲、乙、丙三只蚂蚁所走的最短路径.
图1 图2 图3
图1中AM2=82+92=145.
图2中AM2=52+122=169.
图3中AM2=132+42=185.
因为145<169<185,
所以蚂蚁甲最先到达,蚂蚁丙最后到达.
6.A 当人走到点D的位置,头顶C与点A的距离是5 m时,灯刚好自动发光,作CE⊥AB于E,由题意可知,BE=CD=1.5 m,AE=AB-BE=4.5-1.5=3 m,AC=5 m,
在Rt△ACE中,CE2=AC2-AE2=52-32=16,
∴CE=4 m.
故学生走到离墙4 m远时,灯刚好发光,
故选A.
7.解析 如图,设OA=x尺,根据题意,得OB=OA=x尺,BC=10尺,
OC=(x-4)尺,
在Rt△OCB中,CO2+CB2=OB2,
即(x-4)2+102=x2,
解得x=14.5,
所以索长为14.5尺.
能力提升全练
8.B 设竹子折断处离地面x尺,则斜边为(10-x)尺,
根据勾股定理得x2+32=(10-x)2,
解得x=4.55.
所以原处还有4.55尺高的竹子.
故选B.
9.(x-6.8)2+x2=102
解析 因为门高AB为x尺,所以门宽BC为(x-6.8)尺,依题意得BC2+AB2=AC2,∵AC=1丈=10尺,
∴(x-6.8)2+x2=102.故答案为(x-6.8)2+x2=102.
10.20
解析 如图,将杯子侧面展开,作A关于EF的对称点A',
连接A'B,作A'D⊥BE,交BE的延长线于D,则A'B的长即为最短距离,A'B2=A'D2+BD2=162+122=202,
所以 A'B=20 cm,故答案为20.
11.解析 在Rt△ABD中,根据勾股定理,得BD2=AB2-AD2=1002-602=6 400,∴BD=80 km,∵80÷20=4(h),
∴台风中心经过4小时从B点移动到D点.
如图,∵距台风中心30 km的圆形区域内都会受到台风的影响,∴游人要在台风中心到达E点之前撤离,
∵BE=BD-DE=80-30=50 km,=2.5(h),
∴游人在接到台风警报后2.5小时内撤离才可脱离危险.
素养探究全练
12.解析 (1)∵∠ACB=90°,∴BC2=AB2-AC2=102-62=64,∴BC=8(cm).
当△ABP为直角三角形时,可分为两种情况进行讨论:
①当∠APB=90°时,点P与点C重合,此时BP=BC=8 cm,∴t=8÷1=8.
②当∠BAP=90°时,BP=t cm,CP=(t-8)cm,
在Rt△ACP中,AP2=62+(t-8)2,在Rt△BAP中,AB2+AP2=BP2,
即102+[62+(t-8)2]=t2,解得t=.
综上所述,当△ABP为直角三角形时,t=8或.
(2)由(1)可知,BC=8 cm.
当△ABP为等腰三角形时,可分三种情况进行讨论:
①当AB=AP时,BP=2BC=16 cm,即t=16;
②当BP=BA=10 cm时,t=10;
③当PA=PB时,如图,设BP=PA=x cm,则PC=(8-x)cm,
在Rt△ACP中,由勾股定理得PC2+AC2=AP2,
∴(8-x)2+62=x2,解得x=,∴BP= cm.∴t=.
综上所述,当△ABP为等腰三角形时,t的值为16或10或.
13.解析 如图为该灯罩的展开图,在Rt△ABC中,
因为AC=36 cm,BC=108÷4=27(cm),
所以由勾股定理,得AB2=AC2+BC2=362+272=2 025=452,
所以AB=45 cm,
所以应裁剪45×4=180 cm的油纸.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
