24.1.2 垂直于弦的直径课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案)
文档属性
| 名称 | 24.1.2 垂直于弦的直径课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 457.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 20:40:17 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册课堂同步练
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
要点梳理
1. 圆是轴对称图形,任何一条直径 都是它的对称轴.
2. 垂直于弦的直径 ,并且 .
3. 平分 的直径 ,并且 .
4. 圆既是中心对称图形,又是轴对称图形,它的对称轴的条数为 条.
基础过关练
1. 小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃残片的边缘描出了点A,B,C,绘出三角形ABC,则这块玻璃镜的圆心是( )
A.AB,AC边上的中线的交点 B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点 D.∠BAC与∠ABC的角平分线的交点
2. 为了测量一铁球的直径,将该铁球放入工作槽内,测得有关数据如图(单位:cm),则该铁球的直径为( )
A.12cm B.8cm C.6cm D.10cm
3. 如图,AB是☉O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )
A. B.2 C.6 D.8
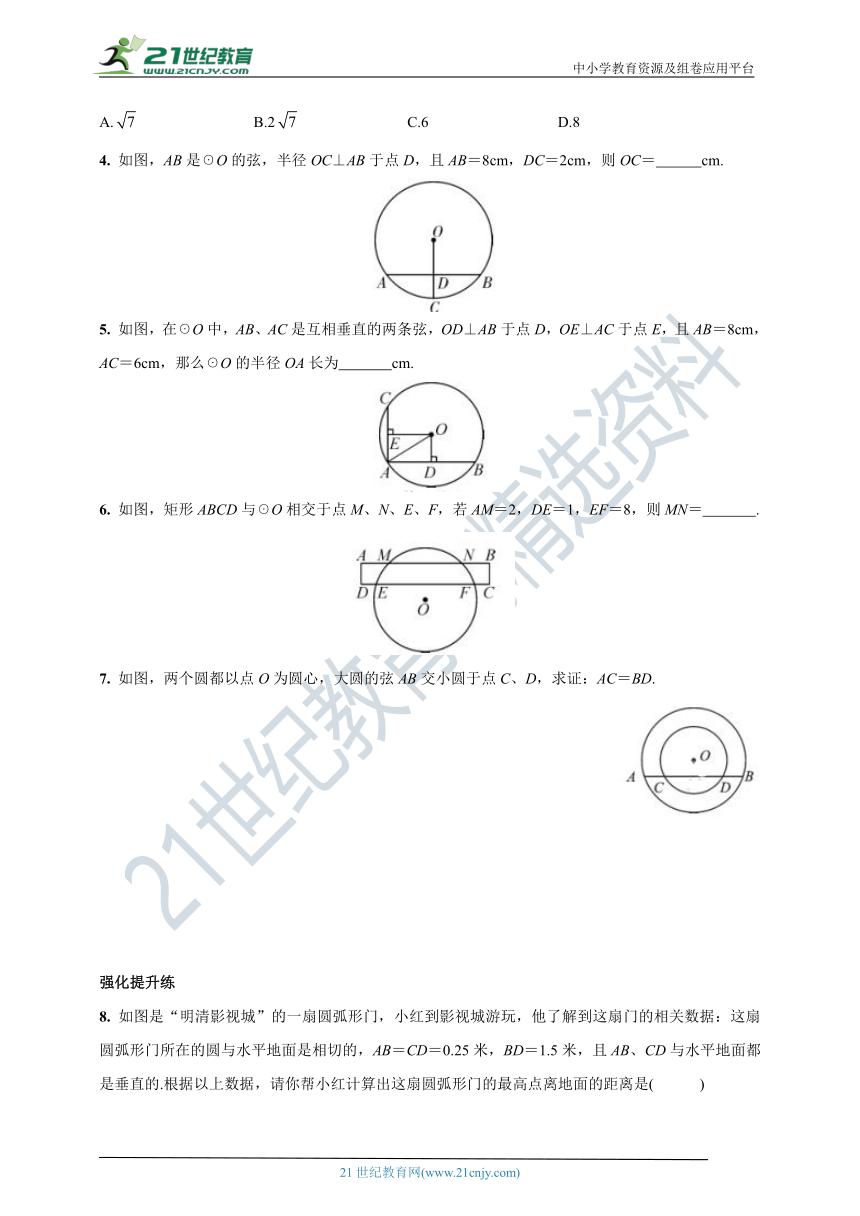
4. 如图,AB是☉O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC= cm.
5. 如图,在☉O中,AB、AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8cm,AC=6cm,那么☉O的半径OA长为 cm.
6. 如图,矩形ABCD与☉O相交于点M、N、E、F,若AM=2,DE=1,EF=8,则MN= .
7. 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于点C、D,求证:AC=BD.
强化提升练
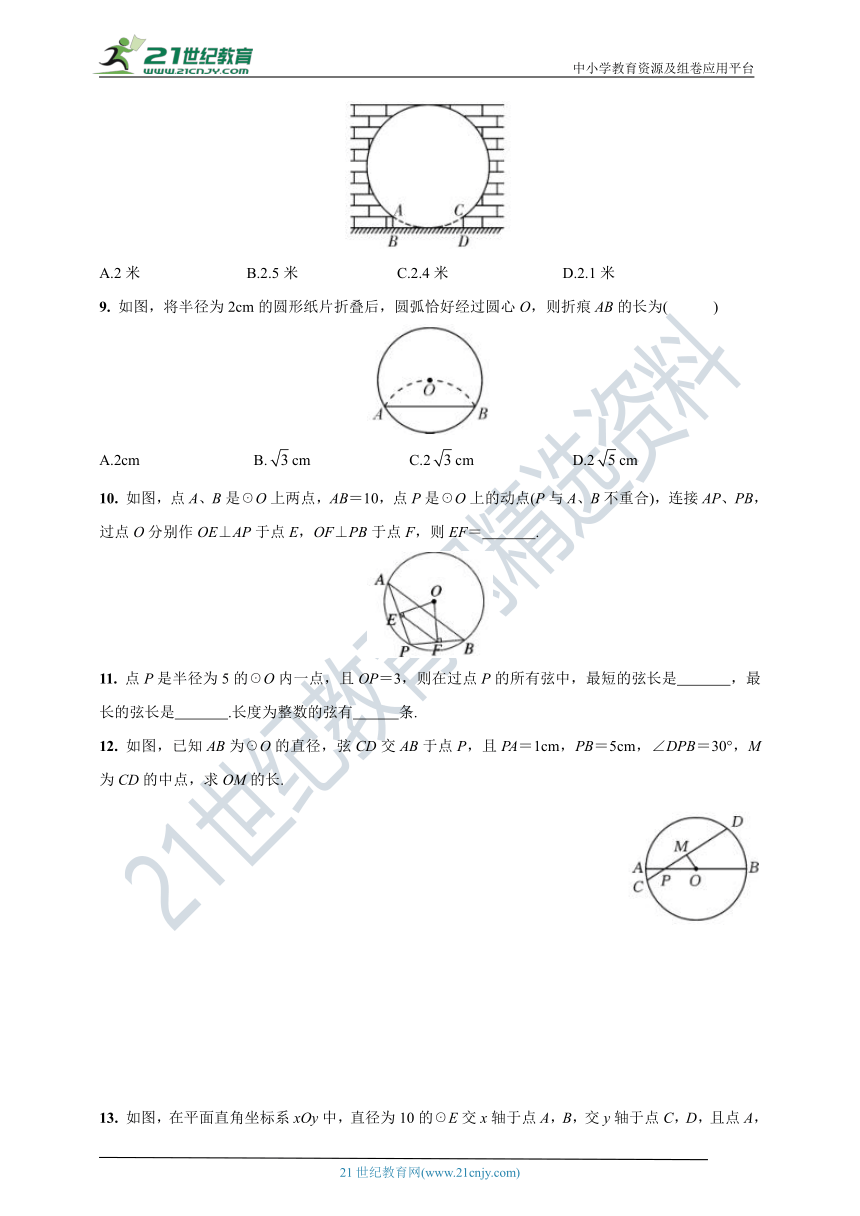
8. 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2米 B.2.5米 C.2.4米 D.2.1米
9. 如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A.2cm B.cm C.2cm D.2cm
10. 如图,点A、B是☉O上两点,AB=10,点P是☉O上的动点(P与A、B不重合),连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= .
11. 点P是半径为5的☉O内一点,且OP=3,则在过点P的所有弦中,最短的弦长是 ,最长的弦长是 .长度为整数的弦有 条.
12. 如图,已知AB为☉O的直径,弦CD交AB于点P,且PA=1cm,PB=5cm,∠DPB=30°,M为CD的中点,求OM的长.
13. 如图,在平面直角坐标系xOy中,直径为10的☉E交x轴于点A,B,交y轴于点C,D,且点A,B的坐标分别为(-2,0),(4,0).试求圆心E和点C,D的坐标.
14. ☉O的半径为5cm,弦AB=8cm,CD=6cm,且AB∥CD,求两弦之间的距离.
延伸拓展练
15. 如图,某地有一座圆弧形拱桥,圆心为点O,桥下水面跨度为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m,现有一艘宽3m、船舱顶部为长方形并高出水面AB2m的货船要经过拱桥.问此货船能否顺利地通过这座拱桥
参 考 答 案
要点梳理
1. 所在直线 2. 平分弦 平分弦所对的两条弧 3. 弦(不是直径) 垂直于弦 平分弦所对的两条弧
4. 无数
基础过关练
1. B 2. D 3. B
4. 5 5. 5
6. 6
7. 解:过点O作OM⊥AB,垂足为M,由垂径定理可得MA=MB,MC=MD,故AC=BD.
强化提升练
8. B 9. C
10. 5
11. 8 10 4
12. 解:∵M为CD的中点,∴OM⊥CD,∵AP=1cm,PB=5cm,∴AO=BO=AB=3cm,则OP=AO-AP=2cm. 在Rt△MOP中,∠DPB=30°,∴OM=OP=1cm.
13. 解:作EF⊥x轴,交x轴于点F,连接EB,∵A,B的坐标分别为(-2,0),(4,0),∴AB=6,OB=4,∴BF=3,∴OF=1,∵⊙E的直径为10,∴半径EB=5,∴EF=4,∴E的坐标是(1,4). 作EG⊥y轴,交y轴于点G,连接EC,ED,由勾股定理得CG==2,∴点C的坐标是(0,4+2),点D的坐标是(0,4-2).
14. 解:①如图1,过点O作ON⊥CD,垂足为N,交AB于点M.∵AB∥CD,∴ON⊥AB. ∴ND=×6=3,MB=×8=4. 连接OB、OD,则在Rt△OMB中,OM===3. 同理可得ON=4,∴MN=4-3=1(cm). ②如图2,同①可得OM=3,ON=4,则有MN=4+3=7(cm).∴AB与CD之间的距离为1cm或7cm.
图1 图2
延伸拓展练
15. 解:连接OA、ON,设CD交MN于点H.AB=7.2m,CD=2.4m,EF=3m,且D为AB、EF的中点,OC⊥AB,OC⊥MN.设OA=R,则OD=OC-DC=R-2.4,AD=AB=3.6m. 在Rt△OAD中,有OA2=AD2+OD2,即R2=3.62+(R-2.4)2,解得R=3.9m.在Rt△ONH中,OH===3.6m,∴FN=DH=OH-OD=3.6-(3.9-2.4)=2.1m>2m. ∴货船可以顺利通过这座拱桥,但要非常小心.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级上册课堂同步练
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
要点梳理
1. 圆是轴对称图形,任何一条直径 都是它的对称轴.
2. 垂直于弦的直径 ,并且 .
3. 平分 的直径 ,并且 .
4. 圆既是中心对称图形,又是轴对称图形,它的对称轴的条数为 条.
基础过关练
1. 小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃残片的边缘描出了点A,B,C,绘出三角形ABC,则这块玻璃镜的圆心是( )
A.AB,AC边上的中线的交点 B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点 D.∠BAC与∠ABC的角平分线的交点
2. 为了测量一铁球的直径,将该铁球放入工作槽内,测得有关数据如图(单位:cm),则该铁球的直径为( )
A.12cm B.8cm C.6cm D.10cm
3. 如图,AB是☉O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )
A. B.2 C.6 D.8
4. 如图,AB是☉O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC= cm.
5. 如图,在☉O中,AB、AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8cm,AC=6cm,那么☉O的半径OA长为 cm.
6. 如图,矩形ABCD与☉O相交于点M、N、E、F,若AM=2,DE=1,EF=8,则MN= .
7. 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于点C、D,求证:AC=BD.
强化提升练
8. 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
A.2米 B.2.5米 C.2.4米 D.2.1米
9. 如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A.2cm B.cm C.2cm D.2cm
10. 如图,点A、B是☉O上两点,AB=10,点P是☉O上的动点(P与A、B不重合),连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF= .
11. 点P是半径为5的☉O内一点,且OP=3,则在过点P的所有弦中,最短的弦长是 ,最长的弦长是 .长度为整数的弦有 条.
12. 如图,已知AB为☉O的直径,弦CD交AB于点P,且PA=1cm,PB=5cm,∠DPB=30°,M为CD的中点,求OM的长.
13. 如图,在平面直角坐标系xOy中,直径为10的☉E交x轴于点A,B,交y轴于点C,D,且点A,B的坐标分别为(-2,0),(4,0).试求圆心E和点C,D的坐标.
14. ☉O的半径为5cm,弦AB=8cm,CD=6cm,且AB∥CD,求两弦之间的距离.
延伸拓展练
15. 如图,某地有一座圆弧形拱桥,圆心为点O,桥下水面跨度为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m,现有一艘宽3m、船舱顶部为长方形并高出水面AB2m的货船要经过拱桥.问此货船能否顺利地通过这座拱桥
参 考 答 案
要点梳理
1. 所在直线 2. 平分弦 平分弦所对的两条弧 3. 弦(不是直径) 垂直于弦 平分弦所对的两条弧
4. 无数
基础过关练
1. B 2. D 3. B
4. 5 5. 5
6. 6
7. 解:过点O作OM⊥AB,垂足为M,由垂径定理可得MA=MB,MC=MD,故AC=BD.
强化提升练
8. B 9. C
10. 5
11. 8 10 4
12. 解:∵M为CD的中点,∴OM⊥CD,∵AP=1cm,PB=5cm,∴AO=BO=AB=3cm,则OP=AO-AP=2cm. 在Rt△MOP中,∠DPB=30°,∴OM=OP=1cm.
13. 解:作EF⊥x轴,交x轴于点F,连接EB,∵A,B的坐标分别为(-2,0),(4,0),∴AB=6,OB=4,∴BF=3,∴OF=1,∵⊙E的直径为10,∴半径EB=5,∴EF=4,∴E的坐标是(1,4). 作EG⊥y轴,交y轴于点G,连接EC,ED,由勾股定理得CG==2,∴点C的坐标是(0,4+2),点D的坐标是(0,4-2).
14. 解:①如图1,过点O作ON⊥CD,垂足为N,交AB于点M.∵AB∥CD,∴ON⊥AB. ∴ND=×6=3,MB=×8=4. 连接OB、OD,则在Rt△OMB中,OM===3. 同理可得ON=4,∴MN=4-3=1(cm). ②如图2,同①可得OM=3,ON=4,则有MN=4+3=7(cm).∴AB与CD之间的距离为1cm或7cm.
图1 图2
延伸拓展练
15. 解:连接OA、ON,设CD交MN于点H.AB=7.2m,CD=2.4m,EF=3m,且D为AB、EF的中点,OC⊥AB,OC⊥MN.设OA=R,则OD=OC-DC=R-2.4,AD=AB=3.6m. 在Rt△OAD中,有OA2=AD2+OD2,即R2=3.62+(R-2.4)2,解得R=3.9m.在Rt△ONH中,OH===3.6m,∴FN=DH=OH-OD=3.6-(3.9-2.4)=2.1m>2m. ∴货船可以顺利通过这座拱桥,但要非常小心.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
