24.1.3 弧、弦、圆心角课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案)
文档属性
| 名称 | 24.1.3 弧、弦、圆心角课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 484.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 20:41:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册课堂同步练
第二十四章 圆
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
要点梳理
1. 的角,叫做圆心角.
2. 在 中,相等的圆心角所对的弧 ,所对的弦 .
3. 在 中,两个圆心角、两条弧、两条弦中如果有一组量相等,则它们所对应的其余各组量 .
基础过关练
1. 下列图形中表示的角是圆心角的是( )
2. 下列说法中,正确的是( )
A.等弦所对的弧相等 B.同圆或等圆中,等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等,所对的圆心角相等
3. 一弧长是所在圆周长的,那么该弧所对圆心角为( )
A.136° B.150° C.216° D.250°
4. 如图,AB是直径,==,∠BOC=40°,则∠AOE= .
5. 如图,D、E分别是☉O的半径OA、OB上的点,CD⊥OA,CE⊥OB,CD=CE,则与的大小关系是 .
6. AB与DE是☉O的直径,C是☉O上一点,AC∥DE.
求证:(1)=;
(2)BE=EC.
强化提升练
7. 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则所对的圆心角的度数为( )
A.40° B.50° C.60° D.70°
8. 如图,AB,CD分别为☉O的两条弦,OM⊥AB于点M,ON⊥CD于点N,且OM=ON,则( )
A.AB=CD B.∠AOB=∠COD C.= D.以上结论都对
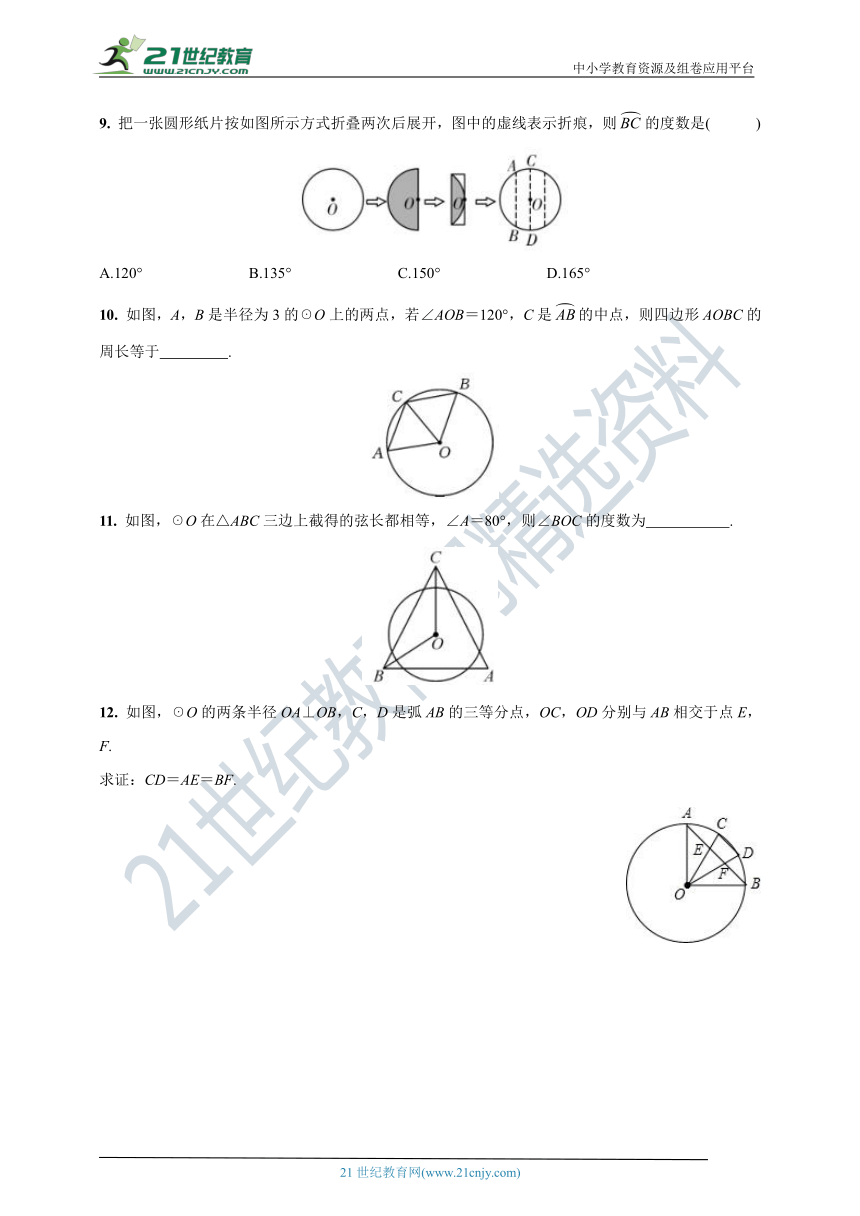
9. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120° B.135° C.150° D.165°
10. 如图,A,B是半径为3的☉O上的两点,若∠AOB=120°,C是的中点,则四边形AOBC的周长等于 .
11. 如图,☉O在△ABC三边上截得的弦长都相等,∠A=80°,则∠BOC的度数为 .
12. 如图,☉O的两条半径OA⊥OB,C,D是弧AB的三等分点,OC,OD分别与AB相交于点E,F.
求证:CD=AE=BF.
13. 如图,在☉O中,AB是直径,CO⊥AB,点D是CO的中点,DE∥AB,求证:=2.
14. 如图,AB是☉O的直径,=,∠COD=60°.
(1)△AOC是等边三角形吗 请说明理由;
(2)求证:OC∥BD.
延伸拓展练
15. 如图,点A是半圆上的一个三等分点,点B是的中点,点P是直径MN上一个动点,圆O的半径为1.
(1)找出当AP+BP能得到最小值时点P的位置;
(2)求出AP+BP的最小值.
参 考 答 案
要点梳理
1. 顶点在圆心 2. 同圆或等圆 相等 相等 3. 同圆或等圆 也相等
基础过关练
1. A 2. B 3. C
4. 60°
5. 相等
6. 证明:(1)连接OC,∵AC∥DE,∴∠AOD=∠OAC,∠COE=∠OCA,∵OA=OC,∴∠OAC=∠OCA,∴∠AOD=∠COE,∴=.
(2)∵∠AOD=∠BOE,∠AOD=∠COE,∴∠BOE=∠COE,∴BE=CE.
强化提升练
7. B 8. D 9. C
10. 12
11. 130°
12. 证明:连接AC、BD,∵C,D是弧AB的三等分点,∴AC=CD=BD. ∵∠AOC=∠COD,OA=OC=OD,∴△ACO≌△DCO,∴∠ACO=∠DCO. ∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=(180°-30°)÷2=75°,∴∠OEF=∠OCD,∴CD∥AB,∴∠AEC=∠OCD,∴∠ACO=∠AEC,故AC=AE.同理,BF=BD. 又∵AC=CD=BD,∴CD=AE=BF.
13. 证明:过点O作OF⊥CE交⊙O于点F. ∵CO⊥AB,DE∥AB,∴CO⊥DE. 又∵点D是CO的中点,∴EC=EO=CO. ∴△COE是等边三角形. ∵OF⊥CE,∴∠COF=∠EOF=30°. 又∵∠COE=60°,∠COB=90°,∴∠EOB=30°. ∴==,∴=2.
14. (1)解:△AOC是等边三角形.
理由:∵=,∴∠AOC=∠COD=60°,又∵OA=OC,∴△AOC是等边三角形;
(2)证明:∵∠AOC=∠COD=60°,∴∠BOD=180°-(∠AOC+∠COD)=60°. ∵OD=OB,∴△ODB为等边三角形. ∴∠ODB=60°,∴∠ODB=∠COD=60°.∴OC∥BD.
延伸拓展练
15. 解:(1)如图,过A作AA′⊥MN于E,连接BA′. ∴P位于A′B与MN的交点处.
(2)如图,连接OB、OA′,∵点A是半圆上的一个三等分点,∴∠AON=∠A′ON=60°,∵点B是的中点,∴∠BON=30°,∴∠BOA′=∠A′ON+∠BON=90°,∵OB=OA′=1,∴BA′=,即AP+BP最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级上册课堂同步练
第二十四章 圆
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
要点梳理
1. 的角,叫做圆心角.
2. 在 中,相等的圆心角所对的弧 ,所对的弦 .
3. 在 中,两个圆心角、两条弧、两条弦中如果有一组量相等,则它们所对应的其余各组量 .
基础过关练
1. 下列图形中表示的角是圆心角的是( )
2. 下列说法中,正确的是( )
A.等弦所对的弧相等 B.同圆或等圆中,等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等,所对的圆心角相等
3. 一弧长是所在圆周长的,那么该弧所对圆心角为( )
A.136° B.150° C.216° D.250°
4. 如图,AB是直径,==,∠BOC=40°,则∠AOE= .
5. 如图,D、E分别是☉O的半径OA、OB上的点,CD⊥OA,CE⊥OB,CD=CE,则与的大小关系是 .
6. AB与DE是☉O的直径,C是☉O上一点,AC∥DE.
求证:(1)=;
(2)BE=EC.
强化提升练
7. 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则所对的圆心角的度数为( )
A.40° B.50° C.60° D.70°
8. 如图,AB,CD分别为☉O的两条弦,OM⊥AB于点M,ON⊥CD于点N,且OM=ON,则( )
A.AB=CD B.∠AOB=∠COD C.= D.以上结论都对
9. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120° B.135° C.150° D.165°
10. 如图,A,B是半径为3的☉O上的两点,若∠AOB=120°,C是的中点,则四边形AOBC的周长等于 .
11. 如图,☉O在△ABC三边上截得的弦长都相等,∠A=80°,则∠BOC的度数为 .
12. 如图,☉O的两条半径OA⊥OB,C,D是弧AB的三等分点,OC,OD分别与AB相交于点E,F.
求证:CD=AE=BF.
13. 如图,在☉O中,AB是直径,CO⊥AB,点D是CO的中点,DE∥AB,求证:=2.
14. 如图,AB是☉O的直径,=,∠COD=60°.
(1)△AOC是等边三角形吗 请说明理由;
(2)求证:OC∥BD.
延伸拓展练
15. 如图,点A是半圆上的一个三等分点,点B是的中点,点P是直径MN上一个动点,圆O的半径为1.
(1)找出当AP+BP能得到最小值时点P的位置;
(2)求出AP+BP的最小值.
参 考 答 案
要点梳理
1. 顶点在圆心 2. 同圆或等圆 相等 相等 3. 同圆或等圆 也相等
基础过关练
1. A 2. B 3. C
4. 60°
5. 相等
6. 证明:(1)连接OC,∵AC∥DE,∴∠AOD=∠OAC,∠COE=∠OCA,∵OA=OC,∴∠OAC=∠OCA,∴∠AOD=∠COE,∴=.
(2)∵∠AOD=∠BOE,∠AOD=∠COE,∴∠BOE=∠COE,∴BE=CE.
强化提升练
7. B 8. D 9. C
10. 12
11. 130°
12. 证明:连接AC、BD,∵C,D是弧AB的三等分点,∴AC=CD=BD. ∵∠AOC=∠COD,OA=OC=OD,∴△ACO≌△DCO,∴∠ACO=∠DCO. ∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=(180°-30°)÷2=75°,∴∠OEF=∠OCD,∴CD∥AB,∴∠AEC=∠OCD,∴∠ACO=∠AEC,故AC=AE.同理,BF=BD. 又∵AC=CD=BD,∴CD=AE=BF.
13. 证明:过点O作OF⊥CE交⊙O于点F. ∵CO⊥AB,DE∥AB,∴CO⊥DE. 又∵点D是CO的中点,∴EC=EO=CO. ∴△COE是等边三角形. ∵OF⊥CE,∴∠COF=∠EOF=30°. 又∵∠COE=60°,∠COB=90°,∴∠EOB=30°. ∴==,∴=2.
14. (1)解:△AOC是等边三角形.
理由:∵=,∴∠AOC=∠COD=60°,又∵OA=OC,∴△AOC是等边三角形;
(2)证明:∵∠AOC=∠COD=60°,∴∠BOD=180°-(∠AOC+∠COD)=60°. ∵OD=OB,∴△ODB为等边三角形. ∴∠ODB=60°,∴∠ODB=∠COD=60°.∴OC∥BD.
延伸拓展练
15. 解:(1)如图,过A作AA′⊥MN于E,连接BA′. ∴P位于A′B与MN的交点处.
(2)如图,连接OB、OA′,∵点A是半圆上的一个三等分点,∴∠AON=∠A′ON=60°,∵点B是的中点,∴∠BON=30°,∴∠BOA′=∠A′ON+∠BON=90°,∵OB=OA′=1,∴BA′=,即AP+BP最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
