3.1.1椭圆的定义及其标准方程(第二课时)人教A 版2019(共15张PPT)
文档属性
| 名称 | 3.1.1椭圆的定义及其标准方程(第二课时)人教A 版2019(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 08:54:58 | ||
图片预览






文档简介
(共15张PPT)
第三章 圆锥曲线的方程
3.1.1 椭圆及其标准方程
(第二课时)
学习目标
1 巩固椭圆的定义及椭圆的标准方程;
2 应用椭圆的定义及椭圆的标准方程解决相关问题.
一)新课引入
椭圆的定义及其标准方程之间是什么关系
互为充要条件,可以从方程角度认识椭圆
二)讲授新课
例2 如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P圆上运动时,线段PD的中点M的轨迹是什么?为什么?
分析:设点M(x, y), 点P(x0, y0),由点M是线段PD的中点,得:x0 =x,y0=2x.
由已知,点P(x0, y0)在圆x2+y2=4上
将x0 =x,y0=2x代入x2+y2=4成立。
即x2+4y2=4
两边同除以4得:+y2=1
从方程角度看,+y2=1表示椭圆的焦点在x轴上的标准方程。
思考:如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P圆上运动时,线段PD上点M满足=λ(λ>0且λ≠1),M的轨迹是什么?为什么?
分析:设点M(x, y), 点P(x0, y0),D(x0, 0)
由已知 x=x0 又=λ
(0,y)=λ(0,y0)
∴ x=x0 y0 =
∴ +=1
当 0<λ<1时, <4,+=1 表示焦点在x轴上的椭圆;
当 λ>1时, >4,+=1 表示焦点在y轴上的椭圆.
综上 由圆可以按照某一确定的条件得到椭圆。
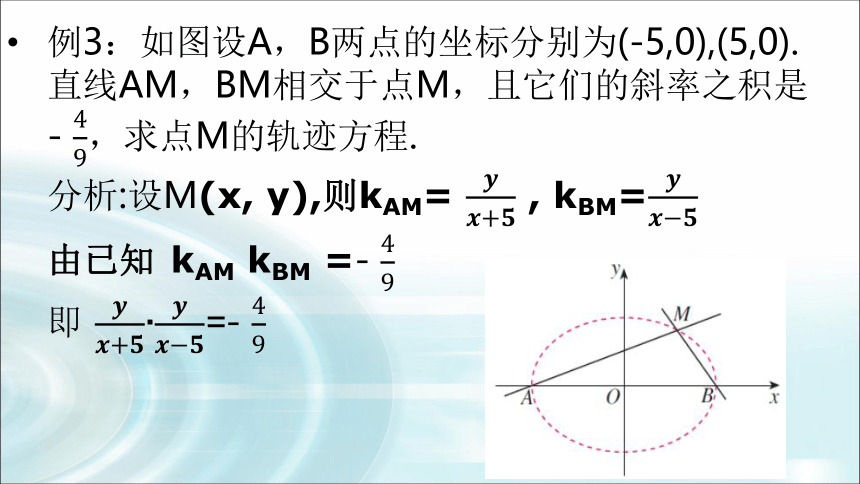
例3:如图设A,B两点的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是
- ,求点M的轨迹方程.
分析:设M(x, y),则kAM= , kBM=
由已知 kAM kBM =-
即 =-
化简得:+=1 焦点在x轴上的椭圆
(除去A,B两点)
思考 如图设A,B两点的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是m(m≠0),求点M的轨迹方程.
分析:设M(x, y),则kAM= , kBM=
由已知 kAM kBM =m 即 =m
化简得:+=1
当-1当m<-1时,+=1表示焦点在y轴上的椭圆;
当m=-1时,+=1表示圆.
综上 一动点与两个定点各确定的两直线的斜率之积是小于0且不等于1的负数时,动点的轨迹是椭圆.
跟踪练习:
1 已知A(0,-1),B(0,1),三角形ABC的周长为6,求顶点C的轨迹方程.
分析:∣AB∣=2,则∣CB∣+∣CA∣=4>∣AB∣=2
则动点C的轨迹是椭圆.
2a=4,a=2;2c=2,c=1;b2 =3;椭圆的焦点在y轴上.
故所求椭圆的方程 :
+=1 (y≠±1)
2如图所示,已知动圆P过定点A(-3,0),
并且在定圆B:(x-3)2+y2=64的内部并且与其内切,求动圆圆心P的轨迹方程.
分析:A(-3,0),B(3,0),
∣PA∣+∣PB∣=16 >∣AB∣=6
∴动圆圆心P的轨迹是椭圆
a=8;c=3;b2 =55;焦点在x轴上。
∴所求椭圆的标准方程:
+=1
3 已知A(-1,0),B(1,0),直线AM,BM相交于点M,且它们的斜率之商是2,M的轨迹是什么?为什么?
分析:设M(x, y),则kAM= , kBM=
kAM =2kBM ,即 =(y≠0)
化简得:2x+2=x-1
x=-3(y≠0)
M的轨迹是两条射线
对于第3题:
如果把“它们的斜率之商是2”改为“它们的斜率之商是m”,其他不变,再求M的轨迹方程。
分析 依新条件得 (m-1)x=-1-m
m=1时,无轨迹;
m≠1时,x=
三 课堂小结
(1) 从方程的角度看是否是椭圆;
(2) 求动点的轨迹要设好动点的坐标(x,y);
(3) 设法寻找动点满足的等式。
四 作业:
课本P109 第 3,4题
第三章 圆锥曲线的方程
3.1.1 椭圆及其标准方程
(第二课时)
学习目标
1 巩固椭圆的定义及椭圆的标准方程;
2 应用椭圆的定义及椭圆的标准方程解决相关问题.
一)新课引入
椭圆的定义及其标准方程之间是什么关系
互为充要条件,可以从方程角度认识椭圆
二)讲授新课
例2 如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P圆上运动时,线段PD的中点M的轨迹是什么?为什么?
分析:设点M(x, y), 点P(x0, y0),由点M是线段PD的中点,得:x0 =x,y0=2x.
由已知,点P(x0, y0)在圆x2+y2=4上
将x0 =x,y0=2x代入x2+y2=4成立。
即x2+4y2=4
两边同除以4得:+y2=1
从方程角度看,+y2=1表示椭圆的焦点在x轴上的标准方程。
思考:如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P圆上运动时,线段PD上点M满足=λ(λ>0且λ≠1),M的轨迹是什么?为什么?
分析:设点M(x, y), 点P(x0, y0),D(x0, 0)
由已知 x=x0 又=λ
(0,y)=λ(0,y0)
∴ x=x0 y0 =
∴ +=1
当 0<λ<1时, <4,+=1 表示焦点在x轴上的椭圆;
当 λ>1时, >4,+=1 表示焦点在y轴上的椭圆.
综上 由圆可以按照某一确定的条件得到椭圆。
例3:如图设A,B两点的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是
- ,求点M的轨迹方程.
分析:设M(x, y),则kAM= , kBM=
由已知 kAM kBM =-
即 =-
化简得:+=1 焦点在x轴上的椭圆
(除去A,B两点)
思考 如图设A,B两点的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是m(m≠0),求点M的轨迹方程.
分析:设M(x, y),则kAM= , kBM=
由已知 kAM kBM =m 即 =m
化简得:+=1
当-1
当m=-1时,+=1表示圆.
综上 一动点与两个定点各确定的两直线的斜率之积是小于0且不等于1的负数时,动点的轨迹是椭圆.
跟踪练习:
1 已知A(0,-1),B(0,1),三角形ABC的周长为6,求顶点C的轨迹方程.
分析:∣AB∣=2,则∣CB∣+∣CA∣=4>∣AB∣=2
则动点C的轨迹是椭圆.
2a=4,a=2;2c=2,c=1;b2 =3;椭圆的焦点在y轴上.
故所求椭圆的方程 :
+=1 (y≠±1)
2如图所示,已知动圆P过定点A(-3,0),
并且在定圆B:(x-3)2+y2=64的内部并且与其内切,求动圆圆心P的轨迹方程.
分析:A(-3,0),B(3,0),
∣PA∣+∣PB∣=16 >∣AB∣=6
∴动圆圆心P的轨迹是椭圆
a=8;c=3;b2 =55;焦点在x轴上。
∴所求椭圆的标准方程:
+=1
3 已知A(-1,0),B(1,0),直线AM,BM相交于点M,且它们的斜率之商是2,M的轨迹是什么?为什么?
分析:设M(x, y),则kAM= , kBM=
kAM =2kBM ,即 =(y≠0)
化简得:2x+2=x-1
x=-3(y≠0)
M的轨迹是两条射线
对于第3题:
如果把“它们的斜率之商是2”改为“它们的斜率之商是m”,其他不变,再求M的轨迹方程。
分析 依新条件得 (m-1)x=-1-m
m=1时,无轨迹;
m≠1时,x=
三 课堂小结
(1) 从方程的角度看是否是椭圆;
(2) 求动点的轨迹要设好动点的坐标(x,y);
(3) 设法寻找动点满足的等式。
四 作业:
课本P109 第 3,4题
