3.1.2椭圆的简单几何性质(第一课时)人教A 版2019(共15张PPT)
文档属性
| 名称 | 3.1.2椭圆的简单几何性质(第一课时)人教A 版2019(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 09:01:26 | ||
图片预览



文档简介
(共15张PPT)
第三章 圆锥曲线的方程
3.1.2 椭圆的简单几何性质
(第一课时)
学习目标
1 理解并掌握椭圆简单几何性质;
2 结合椭圆的定义及椭圆的标准方程理解其简单几何性质.
一)新课引入
从椭圆的标准方程:+=1
可变形为()2 +()2 =1
由此你想到什么?
二)讲授新课
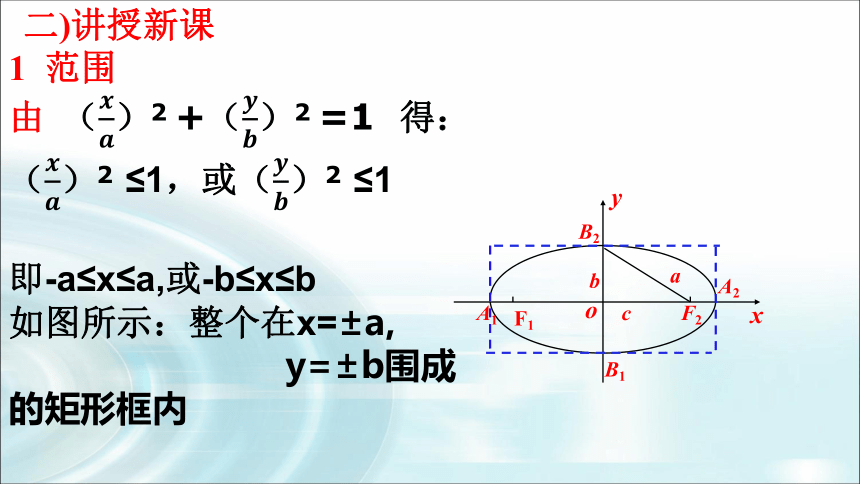
1 范围
由 ()2 +()2 =1 得:
()2 ≤1,或()2 ≤1
即-a≤x≤a,或-b≤x≤b
如图所示:整个在x=±a,
y=±b围成
的矩形框内
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
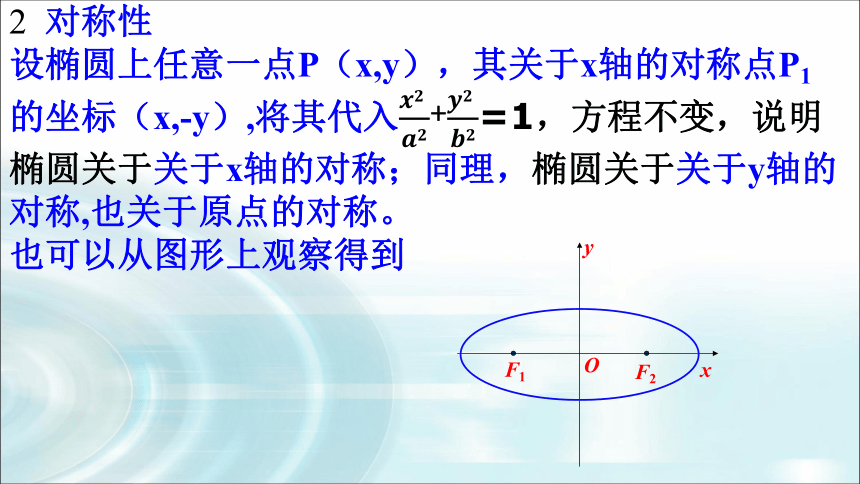
2 对称性
设椭圆上任意一点P(x,y),其关于x轴的对称点P1 的坐标(x,-y),将其代入+=1,方程不变,说明椭圆关于关于x轴的对称;同理,椭圆关于关于y轴的对称,也关于原点的对称。
也可以从图形上观察得到
x
y
O
F1
F2
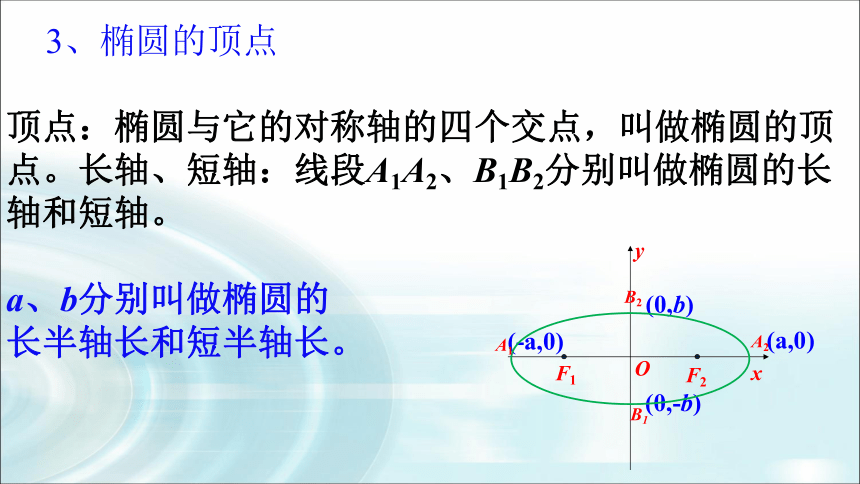
3、椭圆的顶点
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的
长半轴长和短半轴长。
x
y
O
F1
F2
(0,-b)
(0,b)
(-a,0)
(a,0)
A1
A2
B2
B1
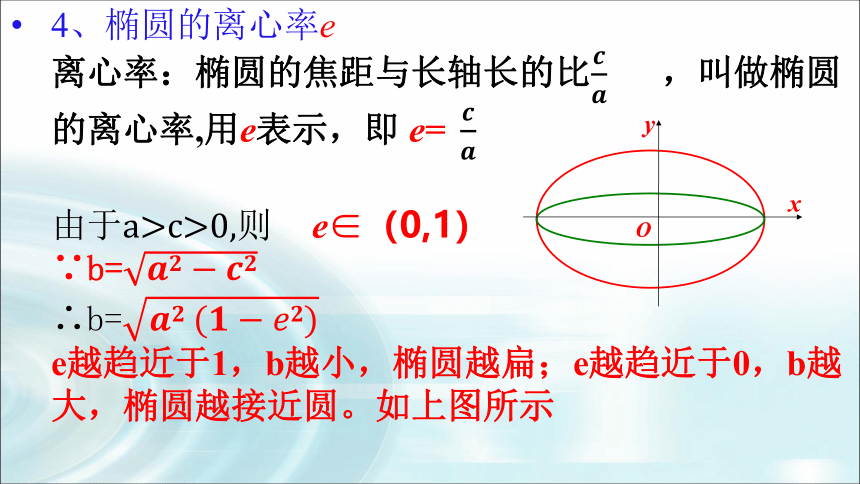
4、椭圆的离心率e
离心率:椭圆的焦距与长轴长的比 ,叫做椭圆的离心率,用e表示,即 e=
由于a>c>0,则 e∈(0,1)
∵b=
∴b=
e越趋近于1,b越小,椭圆越扁;e越趋近于0,b越大,椭圆越接近圆。如上图所示
O
x
y
例1.求椭圆x2+9y2=81的长轴长、短轴长、离心率、焦点和顶点坐标.
分析 把已知方程化成标准方程为 : +=1
得 a=9,b=3,c=6.
所以椭圆的长轴长2a=18,短轴长2b=6,e=
两个焦点的坐标分别为F 1(-3 ,0),
F2(3 ,0).
四个顶点的坐标分别为A1(-9,0),A2(9,0),B1(0,-3),B2(0,3)
例2 求适合下列条件的椭圆的方程:
(1) 长轴长是10,离心率是;
(2) x 轴上的一个焦点与短轴的两个端点的连线互相垂直.焦距是6.
分析 (1)由已知2a=10,a=5;=,c=4.
则b2=9. 若椭圆的焦点在x轴上,椭圆的标准方程是:+=1;
若椭圆的焦点在y轴上,
椭圆的标准方程是:+=1
(2) x 轴上的一个焦点与短轴的两个端点的连线互相垂直.焦距是6.如图
分析:由椭圆的对称性,
x
y
O
F1
F2
A1
A2
ΔA1F2A2 是等腰直角三角形,
则OF2=OA1 =b=c=3
a2=18,所求椭圆的方程:
+=1
三 课堂练习
1 已知椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,则椭圆E的离心率等于( )
2 若椭圆 ,则k=( )
分析:1 已知椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9. 如图,
可能是a+c=9 或a-c=9;
又b=3 , a2=b2+c2
∴a-c=9不能成立。
∴a+c=9 成立
∴c=4
∴a=5
e= =
x
y
O
F1
F2
对于第2题:椭圆
由题意
k+8 >0,当k+8 >9 ,即 k>1时,焦点在x轴上,
a2=k+8, b2 =9, c2 =k-1, ∴e2 == k=4
k+8 >0,当k+8 <9 即-8a2=9,b2 =k+8, c2 =1-k
e2 == k= - 符合条件。
综上 k=4或 k= -
三 课堂小结
(1)椭圆的简单几何性质?
(2)椭圆的标准方程与椭圆的简单几何性质的关系?
四 作业:
课本P112 第 2, 3,,5题
第三章 圆锥曲线的方程
3.1.2 椭圆的简单几何性质
(第一课时)
学习目标
1 理解并掌握椭圆简单几何性质;
2 结合椭圆的定义及椭圆的标准方程理解其简单几何性质.
一)新课引入
从椭圆的标准方程:+=1
可变形为()2 +()2 =1
由此你想到什么?
二)讲授新课
1 范围
由 ()2 +()2 =1 得:
()2 ≤1,或()2 ≤1
即-a≤x≤a,或-b≤x≤b
如图所示:整个在x=±a,
y=±b围成
的矩形框内
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
2 对称性
设椭圆上任意一点P(x,y),其关于x轴的对称点P1 的坐标(x,-y),将其代入+=1,方程不变,说明椭圆关于关于x轴的对称;同理,椭圆关于关于y轴的对称,也关于原点的对称。
也可以从图形上观察得到
x
y
O
F1
F2
3、椭圆的顶点
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的
长半轴长和短半轴长。
x
y
O
F1
F2
(0,-b)
(0,b)
(-a,0)
(a,0)
A1
A2
B2
B1
4、椭圆的离心率e
离心率:椭圆的焦距与长轴长的比 ,叫做椭圆的离心率,用e表示,即 e=
由于a>c>0,则 e∈(0,1)
∵b=
∴b=
e越趋近于1,b越小,椭圆越扁;e越趋近于0,b越大,椭圆越接近圆。如上图所示
O
x
y
例1.求椭圆x2+9y2=81的长轴长、短轴长、离心率、焦点和顶点坐标.
分析 把已知方程化成标准方程为 : +=1
得 a=9,b=3,c=6.
所以椭圆的长轴长2a=18,短轴长2b=6,e=
两个焦点的坐标分别为F 1(-3 ,0),
F2(3 ,0).
四个顶点的坐标分别为A1(-9,0),A2(9,0),B1(0,-3),B2(0,3)
例2 求适合下列条件的椭圆的方程:
(1) 长轴长是10,离心率是;
(2) x 轴上的一个焦点与短轴的两个端点的连线互相垂直.焦距是6.
分析 (1)由已知2a=10,a=5;=,c=4.
则b2=9. 若椭圆的焦点在x轴上,椭圆的标准方程是:+=1;
若椭圆的焦点在y轴上,
椭圆的标准方程是:+=1
(2) x 轴上的一个焦点与短轴的两个端点的连线互相垂直.焦距是6.如图
分析:由椭圆的对称性,
x
y
O
F1
F2
A1
A2
ΔA1F2A2 是等腰直角三角形,
则OF2=OA1 =b=c=3
a2=18,所求椭圆的方程:
+=1
三 课堂练习
1 已知椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,则椭圆E的离心率等于( )
2 若椭圆 ,则k=( )
分析:1 已知椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9. 如图,
可能是a+c=9 或a-c=9;
又b=3 , a2=b2+c2
∴a-c=9不能成立。
∴a+c=9 成立
∴c=4
∴a=5
e= =
x
y
O
F1
F2
对于第2题:椭圆
由题意
k+8 >0,当k+8 >9 ,即 k>1时,焦点在x轴上,
a2=k+8, b2 =9, c2 =k-1, ∴e2 == k=4
k+8 >0,当k+8 <9 即-8
e2 == k= - 符合条件。
综上 k=4或 k= -
三 课堂小结
(1)椭圆的简单几何性质?
(2)椭圆的标准方程与椭圆的简单几何性质的关系?
四 作业:
课本P112 第 2, 3,,5题
