3.1.2椭圆的简单几何性质(第二课时)人教A 版2019(共16张PPT)
文档属性
| 名称 | 3.1.2椭圆的简单几何性质(第二课时)人教A 版2019(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 09:02:11 | ||
图片预览






文档简介
(共16张PPT)
第三章 圆锥曲线的方程
3.1.2 椭圆的简单几何性质
(第二课时)
学习目标
1 巩固对椭圆简单几何性质的理解;
2 会应用椭圆的椭圆简单几何性质解决相关问题.
一)新课引入
椭圆的定义?
椭圆的标准方程?
二)讲授新课
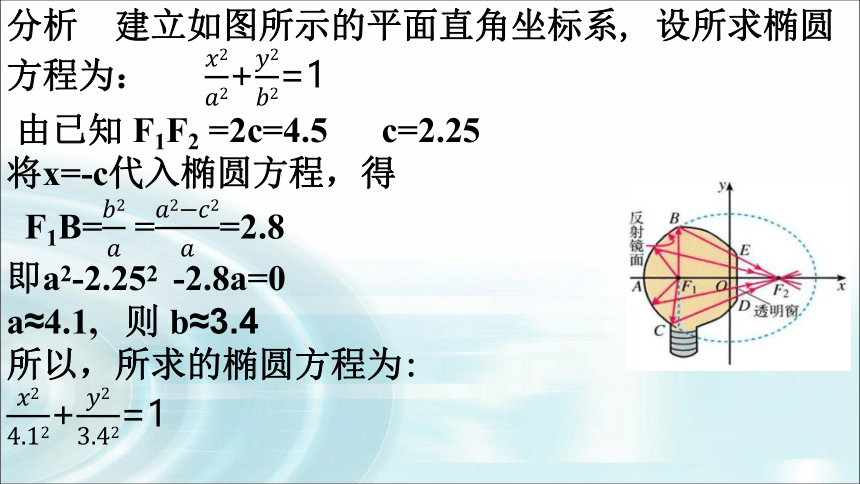
例5 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上, 由椭圆一个焦点F1发出的光线, 经过旋转椭圆面反射后集中到另一个焦点F2 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
分析 建立如图所示的平面直角坐标系, 设所求椭圆方程为: +=1
由已知 F1F2 =2c=4.5 c=2.25
将x=-c代入椭圆方程,得
F1B= ==2.8
即a2-2.252 -2.8a=0
a≈4.1, 则 b≈3.4
所以,所求的椭圆方程为:
+=1
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线
l : x= 的距离的比是常数 求动点M的轨迹.
分析:如图,设d为M到定直线
l : x= 的距离,
由题意,=
= ,两边平方并整理得:
+=1
O
x
y
M
H
F
l
d
这里a2=25,b2=9,c=4,
∴e=
定直线l : x= =
原题可这样叙述:平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线l : x=的距离的比是常数e (0或者 平面内的动点M(x, y)到定点F(-c, 0)的距离与它到定直线l : x=-的距离的比是常数e(0O
x
y
M
H
F
l
d
l′
F′
例7 如图所示,已知直线l :4x-5y+m=0和椭圆C:
+=1,m为何值时,直线l与椭圆C:
(1)有两个公共点?
(2)有且只有一个公共点?
(3)没有公共点
分析:直线与椭圆有无公共点,
相当于由它们联立而成的方程组有无解、有几个解。因此,问题转化为求方程组解的个数的问题。
O
x
y
F2
l
F1
4x-5y+m=0
联立
+=1
得 25x2+8mx+m2-225=0
Δ=36(252-m2)
当Δ>0时,即-5当Δ=0时,即m=±5时,直线与椭圆有一个公共点;当Δ<0时,即m<-5或m>5,直线与椭圆没有公共点。
问题 1 当Δ>0时,即-5设两个交点是A(x1,y1),B(x2,y2)
可以将关于x的一元二次方程
25x2+8mx+m2-225=0的解x1,x2求出,
再利用4x-5y+m=0 求出对应的y1,y2
进而得出两个交点A,B的坐标。再用两点的距离公式,求出∣AB∣的长。
∣AB∣= =∣∣
而已知直线l :4x-5y+m=0的斜率k= ;
∣∣=
那么
∣AB∣=∣∣
=
也就是说,求弦长需要已知弦的斜率,弦的两个端点横坐标和与积。
就本题而言,k= ,
关于x的一元二次方程 25x2+8mx+m2-225=0
=- =
∣AB∣=
我们称其为弦长公式.
问题2 当直线与椭圆相交时,弦的中点的轨迹是什么
依本题,设设两个交点是A(x1,y1),B(x2,y2),线段AB的中点M(x,y)
x1 、x2 满足:
25x2+8mx+m2-225=0
x=,y==-= -
则 y=x
问题3:椭圆的切线方程怎么求
当Δ=0时,即m=±5时,直线与椭圆有一个公共点.这时,直线与椭圆相切,就可以求椭圆的切线方程.
三 课堂小结
(1)椭圆的简单几何性质?
(2)直线与椭圆位置关系?
四 作业:
课本P114 第 5,6题
第三章 圆锥曲线的方程
3.1.2 椭圆的简单几何性质
(第二课时)
学习目标
1 巩固对椭圆简单几何性质的理解;
2 会应用椭圆的椭圆简单几何性质解决相关问题.
一)新课引入
椭圆的定义?
椭圆的标准方程?
二)讲授新课
例5 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上, 由椭圆一个焦点F1发出的光线, 经过旋转椭圆面反射后集中到另一个焦点F2 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
分析 建立如图所示的平面直角坐标系, 设所求椭圆方程为: +=1
由已知 F1F2 =2c=4.5 c=2.25
将x=-c代入椭圆方程,得
F1B= ==2.8
即a2-2.252 -2.8a=0
a≈4.1, 则 b≈3.4
所以,所求的椭圆方程为:
+=1
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线
l : x= 的距离的比是常数 求动点M的轨迹.
分析:如图,设d为M到定直线
l : x= 的距离,
由题意,=
= ,两边平方并整理得:
+=1
O
x
y
M
H
F
l
d
这里a2=25,b2=9,c=4,
∴e=
定直线l : x= =
原题可这样叙述:平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线l : x=的距离的比是常数e (0
x
y
M
H
F
l
d
l′
F′
例7 如图所示,已知直线l :4x-5y+m=0和椭圆C:
+=1,m为何值时,直线l与椭圆C:
(1)有两个公共点?
(2)有且只有一个公共点?
(3)没有公共点
分析:直线与椭圆有无公共点,
相当于由它们联立而成的方程组有无解、有几个解。因此,问题转化为求方程组解的个数的问题。
O
x
y
F2
l
F1
4x-5y+m=0
联立
+=1
得 25x2+8mx+m2-225=0
Δ=36(252-m2)
当Δ>0时,即-5
问题 1 当Δ>0时,即-5
可以将关于x的一元二次方程
25x2+8mx+m2-225=0的解x1,x2求出,
再利用4x-5y+m=0 求出对应的y1,y2
进而得出两个交点A,B的坐标。再用两点的距离公式,求出∣AB∣的长。
∣AB∣= =∣∣
而已知直线l :4x-5y+m=0的斜率k= ;
∣∣=
那么
∣AB∣=∣∣
=
也就是说,求弦长需要已知弦的斜率,弦的两个端点横坐标和与积。
就本题而言,k= ,
关于x的一元二次方程 25x2+8mx+m2-225=0
=- =
∣AB∣=
我们称其为弦长公式.
问题2 当直线与椭圆相交时,弦的中点的轨迹是什么
依本题,设设两个交点是A(x1,y1),B(x2,y2),线段AB的中点M(x,y)
x1 、x2 满足:
25x2+8mx+m2-225=0
x=,y==-= -
则 y=x
问题3:椭圆的切线方程怎么求
当Δ=0时,即m=±5时,直线与椭圆有一个公共点.这时,直线与椭圆相切,就可以求椭圆的切线方程.
三 课堂小结
(1)椭圆的简单几何性质?
(2)直线与椭圆位置关系?
四 作业:
课本P114 第 5,6题
