3.2.1双曲线及其标准方程-人教A 版2019(共15张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程-人教A 版2019(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 09:03:03 | ||
图片预览





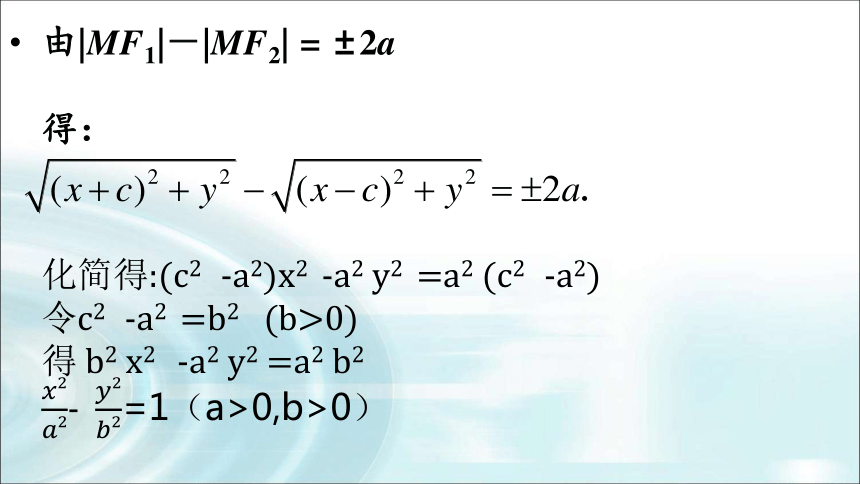
文档简介
(共15张PPT)
第三章 圆锥曲线的方程
3.2.1 双曲线及其标准方程
学习目标
1 了解双曲线的定义及双曲线的标准方程;
2 会应用以上知识解决相关问题.
一)新课引入
椭圆的定义?
构成冷却塔
外形的曲线
形状
二)讲授新课
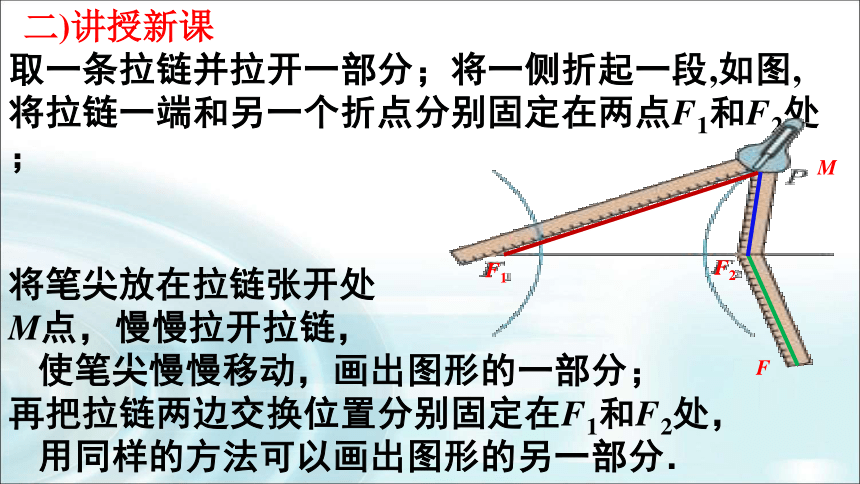
取一条拉链并拉开一部分;将一侧折起一段,如图,
将拉链一端和另一个折点分别固定在两点F1和F2处;
将笔尖放在拉链张开处
M点,慢慢拉开拉链,
使笔尖慢慢移动,画出图形的一部分;
再把拉链两边交换位置分别固定在F1和F2处,
用同样的方法可以画出图形的另一部分.
F
F2
F1
M
所画出的图形就是双曲线.
双曲线的定义:平面上到两个定点F1, F2的距离之差的绝对值为常数(小于|F1F2|)的点的轨迹叫作双曲线.
两个定点F1,F2叫作双曲线的焦点
两个焦点之间的距离|F1F2|叫作焦距
如同建立椭圆方程一样:
取过焦点F1,F2的直线为x轴,
线段F1F2的垂直平分线为y轴,
建立平面直角坐标系
如同建立椭圆方程一样:
取过焦点F1,F2的直线为x轴,
线段F1F2的垂直平分线为y轴,
建立平面直角坐标系 设双曲线的焦距
|F1F2|=2c,双曲线上的点与两定点的距离之差的绝对值为2a (a > 0),则F1,F2的坐标分别为(-c,0),(c,0). 设M(x,y)为双曲线上任意一点,则:
||MF1|-|MF2||=2a,
即 |MF1|-|MF2| = ±2a
由|MF1|-|MF2| = ±2a
得:
化简得:(c2 -a2)x2 -a2 y2 =a2 (c2 -a2)
令c2 -a2 =b2 (b>0)
得 b2 x2 -a2 y2 =a2 b2
- =1(a>0,b>0)
如果焦点在y轴上,同理可得双曲线的方程:
- =1(a>0,b>0)
我们把
- =1(a>0,b>0)
与- =1(a>0,b>0)
都称为双曲线的标准方程,前者是焦点在x轴上的双曲线,后者是焦点在y轴上的双曲线
也由此可知,双曲线的焦点看标准方程的正项
例1 已知双曲线的两个焦点分别为F1(-5,0),F2(5,0),双曲线上一点P到F1, F2的距离之差的绝对值等于6,求该双曲线的标准方程.
分析:由双曲线的定义:2c = 10,2a = 6,
c = 5,a = 3.
则 b = 5 -3 = 16
又焦点在x轴上,双曲线的标准方程:
-=1
例2 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程
分析:设爆炸点P,则∣PA ∣-∣PB∣=680
则P的轨迹是双曲线一支
(∣PA ∣>∣PB∣)
建立如图所示的坐标系。
c=400,a=340,b2 = c2-a2=44400
炮弹爆炸点的轨迹方程
-=1 (x≥340)
三 课堂练习
1.已知双曲线的两个焦点分别为F1(0,-2),F2(0,2),且双曲线经过点P(3,-2),求该双曲线的标准方程.
2 若方程 m x +n y =1表示双曲线, 则实数m,n需要满足什么条件
3 已知双曲线经过点(,-1),(,2) , 求该双曲线的标准方程.
分析 1 由于双曲线的焦点在y轴上
由双曲线的定义知:2a=∣∣PF1∣-∣PF2∣∣=2
∴ a = 1.
又c = 2, ∴b = c -a = 4-1=3.
由于双曲线的焦点在y轴上
所求双曲线的标准方程为
y2-=1
2 mn<0, 方程 m x +n y =1表示双曲线
3.由2,可设双曲线方程 m x +n y =1(mn<0)
将两个点的坐标分别代入m x +n y =1得:
6m+n=1 且 12m+4n=1,解得m=,n=-
即所求双曲线方程 x - y =1
四 课堂小结
(1)双曲线的定义?
(2)双曲线的标准方程?
五 作业:
课本P121 第 2,3,4题
第三章 圆锥曲线的方程
3.2.1 双曲线及其标准方程
学习目标
1 了解双曲线的定义及双曲线的标准方程;
2 会应用以上知识解决相关问题.
一)新课引入
椭圆的定义?
构成冷却塔
外形的曲线
形状
二)讲授新课
取一条拉链并拉开一部分;将一侧折起一段,如图,
将拉链一端和另一个折点分别固定在两点F1和F2处;
将笔尖放在拉链张开处
M点,慢慢拉开拉链,
使笔尖慢慢移动,画出图形的一部分;
再把拉链两边交换位置分别固定在F1和F2处,
用同样的方法可以画出图形的另一部分.
F
F2
F1
M
所画出的图形就是双曲线.
双曲线的定义:平面上到两个定点F1, F2的距离之差的绝对值为常数(小于|F1F2|)的点的轨迹叫作双曲线.
两个定点F1,F2叫作双曲线的焦点
两个焦点之间的距离|F1F2|叫作焦距
如同建立椭圆方程一样:
取过焦点F1,F2的直线为x轴,
线段F1F2的垂直平分线为y轴,
建立平面直角坐标系
如同建立椭圆方程一样:
取过焦点F1,F2的直线为x轴,
线段F1F2的垂直平分线为y轴,
建立平面直角坐标系 设双曲线的焦距
|F1F2|=2c,双曲线上的点与两定点的距离之差的绝对值为2a (a > 0),则F1,F2的坐标分别为(-c,0),(c,0). 设M(x,y)为双曲线上任意一点,则:
||MF1|-|MF2||=2a,
即 |MF1|-|MF2| = ±2a
由|MF1|-|MF2| = ±2a
得:
化简得:(c2 -a2)x2 -a2 y2 =a2 (c2 -a2)
令c2 -a2 =b2 (b>0)
得 b2 x2 -a2 y2 =a2 b2
- =1(a>0,b>0)
如果焦点在y轴上,同理可得双曲线的方程:
- =1(a>0,b>0)
我们把
- =1(a>0,b>0)
与- =1(a>0,b>0)
都称为双曲线的标准方程,前者是焦点在x轴上的双曲线,后者是焦点在y轴上的双曲线
也由此可知,双曲线的焦点看标准方程的正项
例1 已知双曲线的两个焦点分别为F1(-5,0),F2(5,0),双曲线上一点P到F1, F2的距离之差的绝对值等于6,求该双曲线的标准方程.
分析:由双曲线的定义:2c = 10,2a = 6,
c = 5,a = 3.
则 b = 5 -3 = 16
又焦点在x轴上,双曲线的标准方程:
-=1
例2 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程
分析:设爆炸点P,则∣PA ∣-∣PB∣=680
则P的轨迹是双曲线一支
(∣PA ∣>∣PB∣)
建立如图所示的坐标系。
c=400,a=340,b2 = c2-a2=44400
炮弹爆炸点的轨迹方程
-=1 (x≥340)
三 课堂练习
1.已知双曲线的两个焦点分别为F1(0,-2),F2(0,2),且双曲线经过点P(3,-2),求该双曲线的标准方程.
2 若方程 m x +n y =1表示双曲线, 则实数m,n需要满足什么条件
3 已知双曲线经过点(,-1),(,2) , 求该双曲线的标准方程.
分析 1 由于双曲线的焦点在y轴上
由双曲线的定义知:2a=∣∣PF1∣-∣PF2∣∣=2
∴ a = 1.
又c = 2, ∴b = c -a = 4-1=3.
由于双曲线的焦点在y轴上
所求双曲线的标准方程为
y2-=1
2 mn<0, 方程 m x +n y =1表示双曲线
3.由2,可设双曲线方程 m x +n y =1(mn<0)
将两个点的坐标分别代入m x +n y =1得:
6m+n=1 且 12m+4n=1,解得m=,n=-
即所求双曲线方程 x - y =1
四 课堂小结
(1)双曲线的定义?
(2)双曲线的标准方程?
五 作业:
课本P121 第 2,3,4题
