3.2.2双曲线的简单几何性质(第一课时) 课件(共16张PPT)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质(第一课时) 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第三章 圆锥曲线的方程
3.2.2 双曲线的简单几何性质
(第一课时)
学习目标
1 了解双曲线简单几何性质;
2 会结合双曲线理解其几何性质.
一 新课引入
对比椭圆的简单几何性质,双曲线有哪些简单几何性质?
二 讲授新课
1 范围
以 ()2 -()2 =1为例
得:
()2 ≥1,
即x≤-a或x≥a
如图所示,图形在直线x=-a,x=a外侧
两直线x=-a,x=a之间没有图形。
x
O
y
(x,-y)
(x,y)
(-x,y)
(-x,-y)
-a
a
2 对称性
设双曲线上任意一点P(x,y),其关于x轴的对称点P1 的坐标(x,-y),
将其代入- =1,
方程不变,
说明双曲线关于关于x轴的对称;
同理,双曲线关于关于y轴的对称,
也关于原点的对称。
也可以从图形上观察得到
x
O
y
(x,-y)
(x,y)
(-x,y)
(-x,-y)
-a
a
x
y
o
-b
b
-a
a
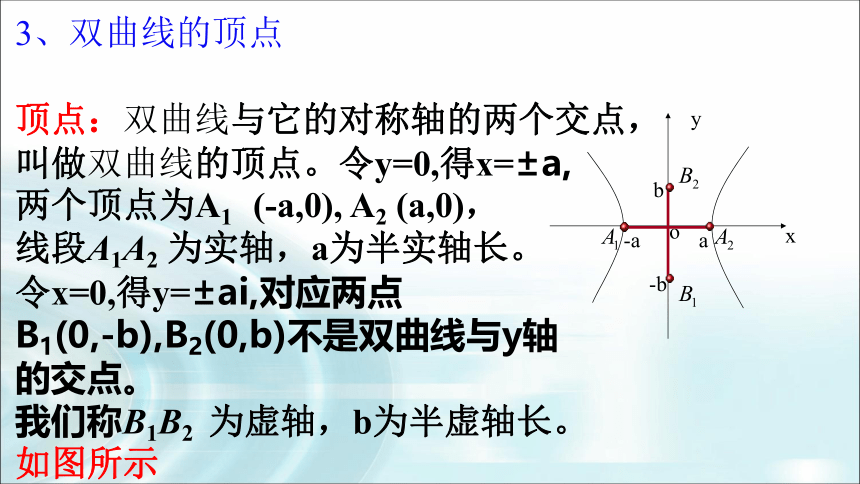
3、双曲线的顶点
顶点:双曲线与它的对称轴的两个交点,
叫做双曲线的顶点。令y=0,得x=±a,
两个顶点为A1 (-a,0), A2 (a,0),
线段A1A2 为实轴,a为半实轴长。
令x=0,得y=±ai,对应两点
B1(0,-b),B2(0,b)不是双曲线与y轴
的交点。
我们称B1B2 为虚轴,b为半虚轴长。
如图所示
M(x,y)
N(x,y’)
Q
x
y
o
a
b
4 渐近线
以 ()2 -()2 =1为例,
双曲线在第一象限的部分对应
方程:y= (x≥a)
令Δy=x- (x≥a)
=(x-)
∵x≥a>0
∴∴Δy>0 即在第一象限,对于任意一个x,
x>
即 直线y=x与曲线y= 在第一象限不相交,并且直线y=x始终在曲线y= 上方。
根据双曲线的对称性,直线y=x与双曲线- =1不相交,两者对于同一个横坐标对应的纵坐标的绝对值始终是前者的比后者的大。
同理,直线y=- x与双曲线- =1也有相同的结论
我们把直线y=x与y=- x称为
双曲线- =1的渐近线。
当a=b时,双曲线- =1为等轴双曲线,
渐近线为y=±x,
这时两条渐近线互相垂直。
5、离心率e
离心率:双曲线的焦距与实轴长的比 ,叫做双曲线离心率,用e表示,即 e=
由于c>a>0,则 e∈(1,+∞)
∵b=
∴=
e越趋近于1,b越小,两渐近线开口越小,双曲线开口也越小;e越大,b越大,两渐近线开口越大,双曲线开口也越大。
例3.求双曲线9y2-16x2=144的实半轴长、虚半轴长、焦点坐标、离心率、渐近线方程..
分析 把已知方程化成标准方程为 : -=1
得 a=4,b=3,c=5.
实半轴长a=4,虚半轴长b=3,
两个焦点的坐标分别为
F 1(0 ,-5), F2(0 ,5).
离心率e=
两个个顶点的坐标分别为A1(0,-4),A2(0,4),
渐近线方程:y= ±x
注 渐近线的求法: 焦点在x轴上时:
将()2 -()2 =1改写为:
()2 -()2 =0
解之得:y=±x
同理,焦点在y轴上时,双曲线的渐近线:
y=±x
三 课堂练习
1、若双曲线的渐近线方程为 y=±x 则双曲线的离心率为 .
双曲线的离心率为2,则两条渐近线方程 .
2求下列双曲线的渐近线方程
(1)4x2-9y2=36,
(2)25x2-4y2=100.
3 双曲线4x2-9y2=36, 上的一点P到右焦点的距离是5,求P到左焦点的距离.
分析:1 讨论焦点的位置.如焦点在x轴上, =,
e== = =
如焦点在y轴上, =
同理可得e=
下一问也要讨论
2 把常数项改为0,表达出y
3 化成标准方程,利用双曲线的定义可求
四 课堂小结
(1)双曲线的简单几何性质?
(2)你对双曲线的渐近线怎样理解,它有什么作用?
五 作业:
课本P114 第 1,2题
第三章 圆锥曲线的方程
3.2.2 双曲线的简单几何性质
(第一课时)
学习目标
1 了解双曲线简单几何性质;
2 会结合双曲线理解其几何性质.
一 新课引入
对比椭圆的简单几何性质,双曲线有哪些简单几何性质?
二 讲授新课
1 范围
以 ()2 -()2 =1为例
得:
()2 ≥1,
即x≤-a或x≥a
如图所示,图形在直线x=-a,x=a外侧
两直线x=-a,x=a之间没有图形。
x
O
y
(x,-y)
(x,y)
(-x,y)
(-x,-y)
-a
a
2 对称性
设双曲线上任意一点P(x,y),其关于x轴的对称点P1 的坐标(x,-y),
将其代入- =1,
方程不变,
说明双曲线关于关于x轴的对称;
同理,双曲线关于关于y轴的对称,
也关于原点的对称。
也可以从图形上观察得到
x
O
y
(x,-y)
(x,y)
(-x,y)
(-x,-y)
-a
a
x
y
o
-b
b
-a
a
3、双曲线的顶点
顶点:双曲线与它的对称轴的两个交点,
叫做双曲线的顶点。令y=0,得x=±a,
两个顶点为A1 (-a,0), A2 (a,0),
线段A1A2 为实轴,a为半实轴长。
令x=0,得y=±ai,对应两点
B1(0,-b),B2(0,b)不是双曲线与y轴
的交点。
我们称B1B2 为虚轴,b为半虚轴长。
如图所示
M(x,y)
N(x,y’)
Q
x
y
o
a
b
4 渐近线
以 ()2 -()2 =1为例,
双曲线在第一象限的部分对应
方程:y= (x≥a)
令Δy=x- (x≥a)
=(x-)
∵x≥a>0
∴
x>
即 直线y=x与曲线y= 在第一象限不相交,并且直线y=x始终在曲线y= 上方。
根据双曲线的对称性,直线y=x与双曲线- =1不相交,两者对于同一个横坐标对应的纵坐标的绝对值始终是前者的比后者的大。
同理,直线y=- x与双曲线- =1也有相同的结论
我们把直线y=x与y=- x称为
双曲线- =1的渐近线。
当a=b时,双曲线- =1为等轴双曲线,
渐近线为y=±x,
这时两条渐近线互相垂直。
5、离心率e
离心率:双曲线的焦距与实轴长的比 ,叫做双曲线离心率,用e表示,即 e=
由于c>a>0,则 e∈(1,+∞)
∵b=
∴=
e越趋近于1,b越小,两渐近线开口越小,双曲线开口也越小;e越大,b越大,两渐近线开口越大,双曲线开口也越大。
例3.求双曲线9y2-16x2=144的实半轴长、虚半轴长、焦点坐标、离心率、渐近线方程..
分析 把已知方程化成标准方程为 : -=1
得 a=4,b=3,c=5.
实半轴长a=4,虚半轴长b=3,
两个焦点的坐标分别为
F 1(0 ,-5), F2(0 ,5).
离心率e=
两个个顶点的坐标分别为A1(0,-4),A2(0,4),
渐近线方程:y= ±x
注 渐近线的求法: 焦点在x轴上时:
将()2 -()2 =1改写为:
()2 -()2 =0
解之得:y=±x
同理,焦点在y轴上时,双曲线的渐近线:
y=±x
三 课堂练习
1、若双曲线的渐近线方程为 y=±x 则双曲线的离心率为 .
双曲线的离心率为2,则两条渐近线方程 .
2求下列双曲线的渐近线方程
(1)4x2-9y2=36,
(2)25x2-4y2=100.
3 双曲线4x2-9y2=36, 上的一点P到右焦点的距离是5,求P到左焦点的距离.
分析:1 讨论焦点的位置.如焦点在x轴上, =,
e== = =
如焦点在y轴上, =
同理可得e=
下一问也要讨论
2 把常数项改为0,表达出y
3 化成标准方程,利用双曲线的定义可求
四 课堂小结
(1)双曲线的简单几何性质?
(2)你对双曲线的渐近线怎样理解,它有什么作用?
五 作业:
课本P114 第 1,2题
