第三章 相互作用 力的合成(共15张PPT)
文档属性
| 名称 | 第三章 相互作用 力的合成(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 949.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-27 11:37:21 | ||
图片预览



文档简介
(共15张PPT)
2.5 力的合成
G=200N
F1
F2
G=200N
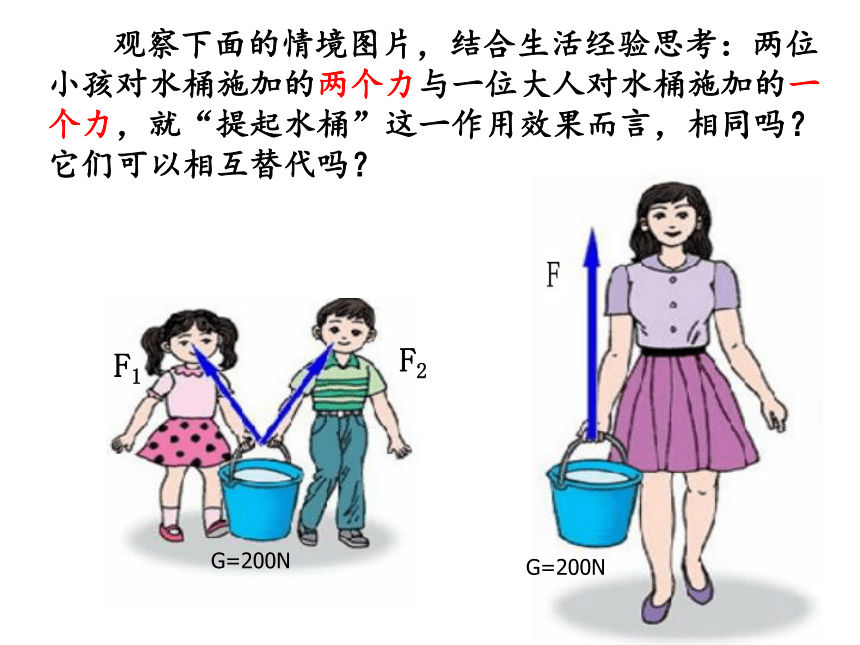
观察下面的情境图片,结合生活经验思考:两位小孩对水桶施加的两个力与一位大人对水桶施加的一个力,就“提起水桶”这一作用效果而言,相同吗?它们可以相互替代吗?
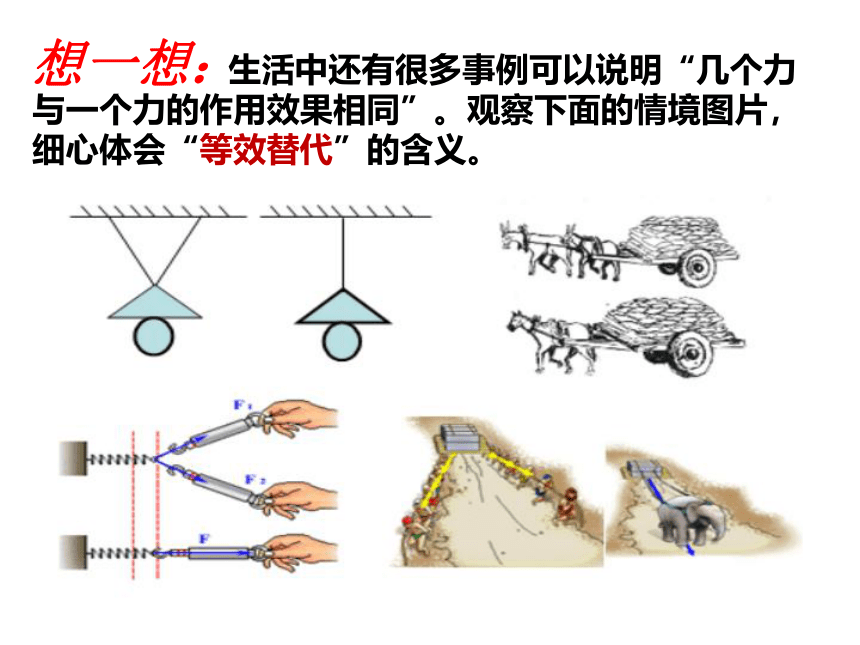
生活中还有很多事例可以说明“几个力与一个力的作用效果相同”。观察下面的情境图片,细心体会“等效替代”的含义。
想一想:
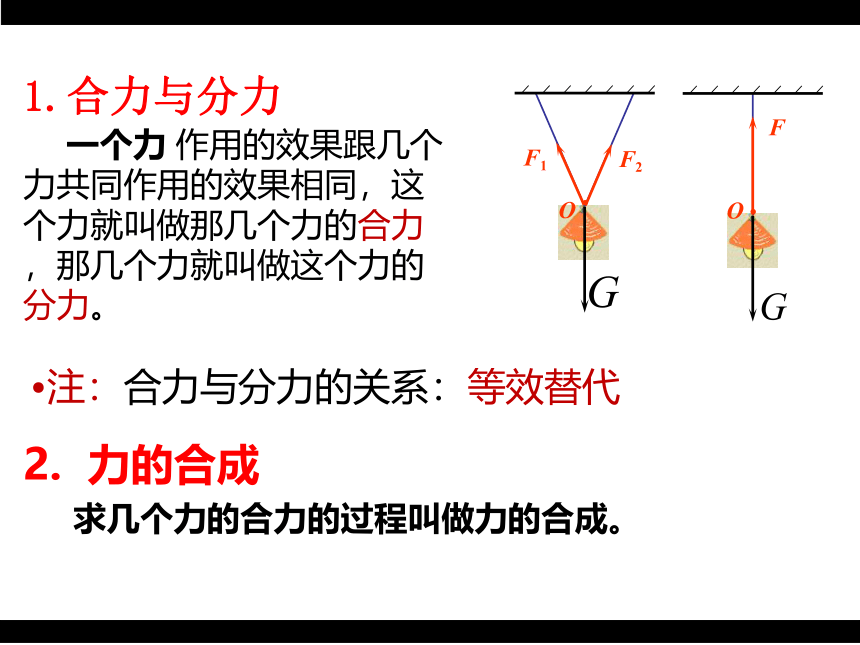
1.合力与分力
一个力 作用的效果跟几个力共同作用的效果相同,这个力就叫做那几个力的合力,那几个力就叫做这个力的分力。
O
.
O
.
F
1
F
2
F
2. 力的合成
求几个力的合力的过程叫做力的合成。
注:合力与分力的关系:等效替代
F1=40N
0
F2=30N
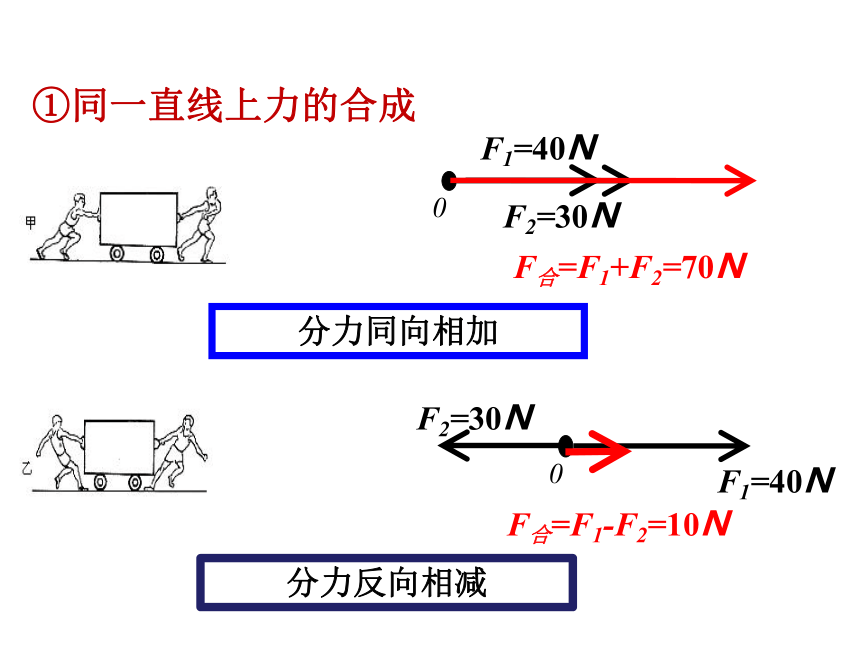
F合=F1+F2=70N
分力同向相加
①同一直线上力的合成
分力反向相减
0
F1=40N
F2=30N
F合=F1-F2=10N
②共点力
作用于物体上的同一点,或者力的作用线相交于同一点的几个力。
作用于一点
作用线交于一点
实验:探究互成角度的共点力合成的规律
问题:①怎样保证合力与分力等效?
②力的大小怎样知道?
③力的方向如何让确定?
F1=10.0 N
F2=6.8 N
F合=12.8 N
O
2N
3、归纳:可见互成角度的两个力的合成,不是简单的将两个力相加减,而是用表示两个力的有向线段为邻边作平行四边形,这两邻边之间的对角线就表示合力的大小和方向。这就叫平行四边形定则.
F1
F
F2
o
虚线
大小:长度
方向:角度
例. 两个共点力间的夹角是90 ,力的大小分别为90 N和120 N,试用作图法和计算法求合力的大小和方向。
F
1
F
2
F
O
30N
53
(2)计算法
解:(1)作图法
1
如图所示,量得合力的大小为150 N, 合力F 与F 的夹角为53 。
4、多力合成的方法:
F1
F2
F3
F4
F12
F123
F1234
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力
逐次合成法
思考:合力是否一定比分力大?
5、合力与分力间的大小关系:
①θ=0°时,即F1、F2共线同方向:
F合=F1+F2 合力方向与两个力的方向相同
②θ=180°时,即F1、F2共线反方向:
F合=|F1-F2| 合力方向与分力F1、F2中较大的方向相同。
④合力的取值范围:|F1-F2| ≤ F合≤ F1+F2
③ F1和F2大小不变时,夹角θ越大,合力就越小:
F合随F1和F2的夹角增大而减小
⑤ F合可能大于、等于、小于 F1、F2
1.关于合力的分力,下列叙述中正确的是( )
A.合力的大小一定大于每一分力的大小
B.合力可以同时垂直于每一分力
C.合力的方向可以与一个分力的方向相反
D.两分力的夹角在0°到180°之间时,夹角越大,则合力越小。
CD
【课堂练习】
2.F1与F2为作用在同一物体上的两个力,F1=10N,F2=8N,它们的合力大小可能是( )
A.19N B.18N C.10N D.2N?
BCD
【课堂练习】
3.有两个大小相等的共点力F1和F2,当它们间的夹角为90°时合力F,则当它们间的夹角为120°时,合力的大小为( )?
A. 2F B.
C. F D. F/2
B
【课堂练习】
2.5 力的合成
G=200N
F1
F2
G=200N
观察下面的情境图片,结合生活经验思考:两位小孩对水桶施加的两个力与一位大人对水桶施加的一个力,就“提起水桶”这一作用效果而言,相同吗?它们可以相互替代吗?
生活中还有很多事例可以说明“几个力与一个力的作用效果相同”。观察下面的情境图片,细心体会“等效替代”的含义。
想一想:
1.合力与分力
一个力 作用的效果跟几个力共同作用的效果相同,这个力就叫做那几个力的合力,那几个力就叫做这个力的分力。
O
.
O
.
F
1
F
2
F
2. 力的合成
求几个力的合力的过程叫做力的合成。
注:合力与分力的关系:等效替代
F1=40N
0
F2=30N
F合=F1+F2=70N
分力同向相加
①同一直线上力的合成
分力反向相减
0
F1=40N
F2=30N
F合=F1-F2=10N
②共点力
作用于物体上的同一点,或者力的作用线相交于同一点的几个力。
作用于一点
作用线交于一点
实验:探究互成角度的共点力合成的规律
问题:①怎样保证合力与分力等效?
②力的大小怎样知道?
③力的方向如何让确定?
F1=10.0 N
F2=6.8 N
F合=12.8 N
O
2N
3、归纳:可见互成角度的两个力的合成,不是简单的将两个力相加减,而是用表示两个力的有向线段为邻边作平行四边形,这两邻边之间的对角线就表示合力的大小和方向。这就叫平行四边形定则.
F1
F
F2
o
虚线
大小:长度
方向:角度
例. 两个共点力间的夹角是90 ,力的大小分别为90 N和120 N,试用作图法和计算法求合力的大小和方向。
F
1
F
2
F
O
30N
53
(2)计算法
解:(1)作图法
1
如图所示,量得合力的大小为150 N, 合力F 与F 的夹角为53 。
4、多力合成的方法:
F1
F2
F3
F4
F12
F123
F1234
先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力
逐次合成法
思考:合力是否一定比分力大?
5、合力与分力间的大小关系:
①θ=0°时,即F1、F2共线同方向:
F合=F1+F2 合力方向与两个力的方向相同
②θ=180°时,即F1、F2共线反方向:
F合=|F1-F2| 合力方向与分力F1、F2中较大的方向相同。
④合力的取值范围:|F1-F2| ≤ F合≤ F1+F2
③ F1和F2大小不变时,夹角θ越大,合力就越小:
F合随F1和F2的夹角增大而减小
⑤ F合可能大于、等于、小于 F1、F2
1.关于合力的分力,下列叙述中正确的是( )
A.合力的大小一定大于每一分力的大小
B.合力可以同时垂直于每一分力
C.合力的方向可以与一个分力的方向相反
D.两分力的夹角在0°到180°之间时,夹角越大,则合力越小。
CD
【课堂练习】
2.F1与F2为作用在同一物体上的两个力,F1=10N,F2=8N,它们的合力大小可能是( )
A.19N B.18N C.10N D.2N?
BCD
【课堂练习】
3.有两个大小相等的共点力F1和F2,当它们间的夹角为90°时合力F,则当它们间的夹角为120°时,合力的大小为( )?
A. 2F B.
C. F D. F/2
B
【课堂练习】
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
