4.2.2 离散型随机变量的分布列 教案(表格式)
文档属性
| 名称 | 4.2.2 离散型随机变量的分布列 教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 515.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 13:52:04 | ||
图片预览



文档简介
课程基本信息
课题 离散型随机变量的分布列
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 2020 年5 月
教学目标
教学目标: 1.理解取有限值的离散型随机变量的分布列的概念与性质. 2.会求出某些简单的离散型随机变量的分布列. 教学重点:离散型随机变量的分布列的概念与性质. 教学难点:离散型随机变量的分布列的概念与性质.
教学过程
时间 教学环节 主要师生活动
1分 知识 回顾 前面我们学习了离散型随机变量,我们先回顾一下。 一般地,如果随机试验的样本空间为,而且对于中的每一个样本点,变量X都对应有唯一确定的实数值,就称X为一个随机变量。对于随机变量X,其所有可能的取值,如果可以一一列举出来,则称X为离散型随机变量。
4分 新知 引入 下面我们来看一个关于离散型随机变量的问题: 尝试与发现: 已知随机变量的取值范围是,而且 , , , (1)求出与的值; (2)如果是给定的实数,则一定可以算出来吗? (3)探讨怎样才能对离散型随机变量有比较全面的了解. 解析: (1)由于只能在0,1,2中取值,所以等价于或, 又因为与互斥, 所以; 类似地,等价于或, 又因为与互斥, 所以; (2)因此,当实数给定时,只要检查是否满足就可以求出. (3) 由此可以看出,对于离散型随机变量来说,如果已知其每一个取值的概率,那么也就可以对其有了比较全面的了解.
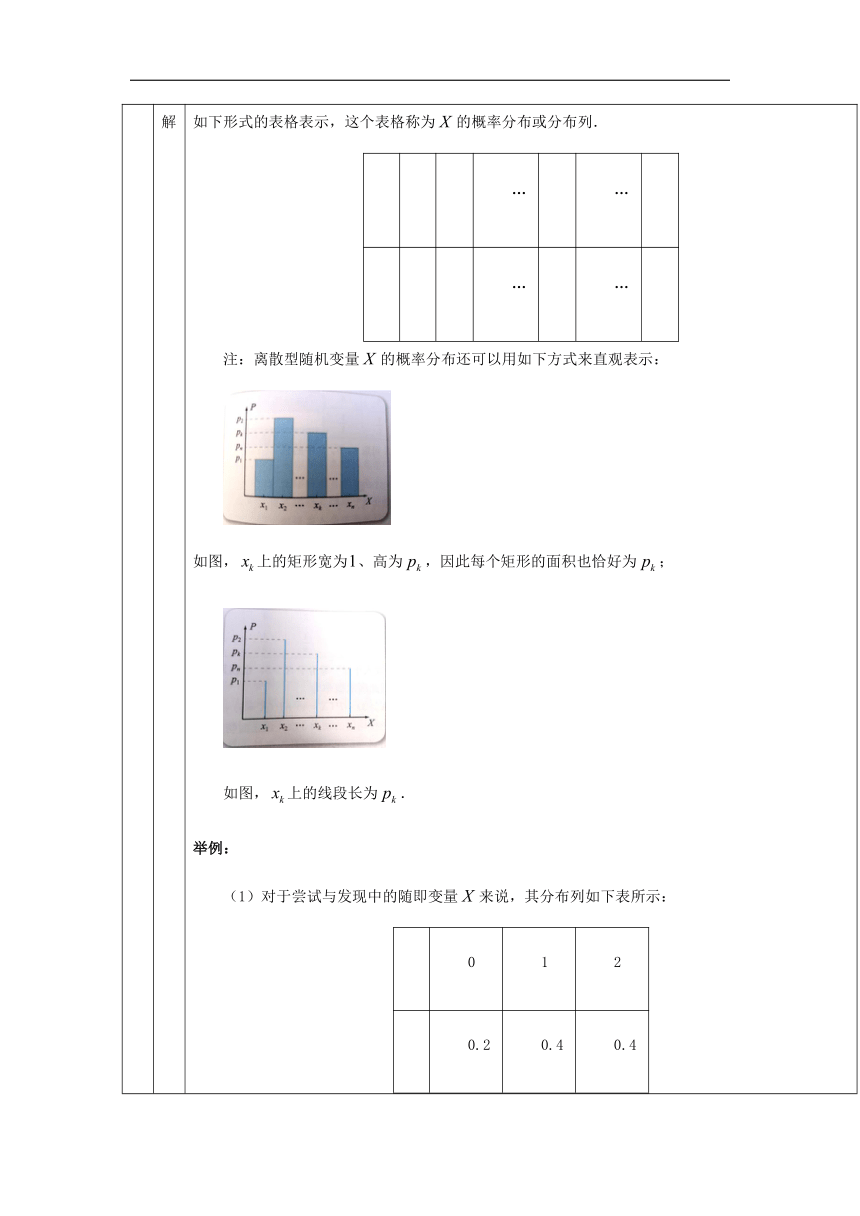
9分 新课 讲解 定义: 一般地,当离散型随机变量的取值范围是,如果对任意,概率 都是已知的,则称的概率分布是已知的.离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列. …… ……
注:离散型随机变量的概率分布还可以用如下方式来直观表示: 如图,上的矩形宽为、高为,因此每个矩形的面积也恰好为; 如图,上的线段长为. 举例: (1)对于尝试与发现中的随即变量来说,其分布列如下表所示: 0 12 0.20.40.4
的概率分布可以用如图直观表示: 剖析: 从离散型随机变量分布列的定义可以看出: 求离散型随机变量的分布列的步骤: (1)找出随机变量X的所有可能的取值(k=1,2,…,n). (2)求出取每一个值的概率P(X=)=. (3)列出表格. 尝试与发现 观察上述分布列的实例,总结离散型随机变量的分布列中应具有的性质. 分析:注意到表示的是事件发生的概率,因此每一个都是非负数;另外,因为分布列给出了随机变量能取的每一个值,而且随机变量取不同的值时的事件是互斥的,因此所有的之和应该等于,即: 离散型随机变量的分布列满足: 性质:(1) ; (2) . 因此我们在求离散型随机变量分布列时应注意的问题 (1)确定离散型随机变量的分布列的关键是要搞清取每一个值对应的随机事件,进一步利用排列、组合知识求出取每一个值的概率.对于随机变量取值较多时,应由简单情况先导出一般的通式,从而简化过程. (2)在求离散型随机变量的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可验证分布列是否正确.
4分 应用 举例 例1 掷一个均匀的骰子,记所得点数为. (1)求的分布列; (2)求“点数大于”的概率. 解 (1)因为的取值范围是 , 而且, 因此的分布列如下表所示.
(2)“点数大于”等价于,也就是说,可取中的任何一个值,因此所求概率为 . 例2 抛一枚均匀的硬币次,设正面朝上的次数为. (1)说明表示的是什么事件,并求出; (2)求的分布列. 解 (1)表示的事件是“恰有次正面朝上”. 因为抛一枚均匀的硬币次,总共有种不同的情况,其中恰有两次正面朝上的情况共有种,所以. (2)根据题意可知,的取值范围是, 又因为用(1)中的方法可知,, 因此的分布列如下表所示.
1分 问题 分析 尝试与发现: 在上一小节中我们已经看到,如果是一个离散型随机变量,都是实数,且,则也是一个离散型随机变量.那么,它们的分布列之间有什么联系? 容易看出,当与都是离散型随机变量而且时,与的分布列如下表所示,它们的第二行的概率值都是一样的. …… ……
…… ……
1分 小结 总结本节课的知识要点,有助于学生落实重点知识与方法。 1、离散型随机变量的分布列 一般地,当离散型随机变量的取值范围是,如果对任意,概率 都是已知的,则称的概率分布是已知的.离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列. …… ……
2、离散型随机变量的分布列的性质 (1) ; (2) . 3、求离散型随机变量的分布列的步骤 (1)找出随机变量X的所有可能的取值(k=1,2,…,n). (2)求出取每一个值的概率P(X=)=. (3)列出表格.
课后 作业 教材P69练习B 2,4,5 1、B-2 某商店购进一批西瓜,预计晴天西瓜畅销,可获利000元;阴天销路一般,可获利00元;下雨天西瓜滞销,会亏损00元. 根据天气预报,未来数日晴天的概率为.2,下雨的概率为.4,试写出销售这批西瓜获利的分布列. 2、B-4抛一枚均匀的硬币次,设正面朝上的次数为. (1)说明表示的是什么事件,并求出 (2)求的分布列. 3、B-5同时抛两个均匀的骰子,设所得点数之和为 (1)写出的分布列; (2)求; (3)求“点数和大于”的概率.
课题 离散型随机变量的分布列
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 2020 年5 月
教学目标
教学目标: 1.理解取有限值的离散型随机变量的分布列的概念与性质. 2.会求出某些简单的离散型随机变量的分布列. 教学重点:离散型随机变量的分布列的概念与性质. 教学难点:离散型随机变量的分布列的概念与性质.
教学过程
时间 教学环节 主要师生活动
1分 知识 回顾 前面我们学习了离散型随机变量,我们先回顾一下。 一般地,如果随机试验的样本空间为,而且对于中的每一个样本点,变量X都对应有唯一确定的实数值,就称X为一个随机变量。对于随机变量X,其所有可能的取值,如果可以一一列举出来,则称X为离散型随机变量。
4分 新知 引入 下面我们来看一个关于离散型随机变量的问题: 尝试与发现: 已知随机变量的取值范围是,而且 , , , (1)求出与的值; (2)如果是给定的实数,则一定可以算出来吗? (3)探讨怎样才能对离散型随机变量有比较全面的了解. 解析: (1)由于只能在0,1,2中取值,所以等价于或, 又因为与互斥, 所以; 类似地,等价于或, 又因为与互斥, 所以; (2)因此,当实数给定时,只要检查是否满足就可以求出. (3) 由此可以看出,对于离散型随机变量来说,如果已知其每一个取值的概率,那么也就可以对其有了比较全面的了解.
9分 新课 讲解 定义: 一般地,当离散型随机变量的取值范围是,如果对任意,概率 都是已知的,则称的概率分布是已知的.离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列. …… ……
注:离散型随机变量的概率分布还可以用如下方式来直观表示: 如图,上的矩形宽为、高为,因此每个矩形的面积也恰好为; 如图,上的线段长为. 举例: (1)对于尝试与发现中的随即变量来说,其分布列如下表所示: 0 12 0.20.40.4
的概率分布可以用如图直观表示: 剖析: 从离散型随机变量分布列的定义可以看出: 求离散型随机变量的分布列的步骤: (1)找出随机变量X的所有可能的取值(k=1,2,…,n). (2)求出取每一个值的概率P(X=)=. (3)列出表格. 尝试与发现 观察上述分布列的实例,总结离散型随机变量的分布列中应具有的性质. 分析:注意到表示的是事件发生的概率,因此每一个都是非负数;另外,因为分布列给出了随机变量能取的每一个值,而且随机变量取不同的值时的事件是互斥的,因此所有的之和应该等于,即: 离散型随机变量的分布列满足: 性质:(1) ; (2) . 因此我们在求离散型随机变量分布列时应注意的问题 (1)确定离散型随机变量的分布列的关键是要搞清取每一个值对应的随机事件,进一步利用排列、组合知识求出取每一个值的概率.对于随机变量取值较多时,应由简单情况先导出一般的通式,从而简化过程. (2)在求离散型随机变量的分布列时,要充分利用分布列的性质,这样不但可以减少运算量,还可验证分布列是否正确.
4分 应用 举例 例1 掷一个均匀的骰子,记所得点数为. (1)求的分布列; (2)求“点数大于”的概率. 解 (1)因为的取值范围是 , 而且, 因此的分布列如下表所示.
(2)“点数大于”等价于,也就是说,可取中的任何一个值,因此所求概率为 . 例2 抛一枚均匀的硬币次,设正面朝上的次数为. (1)说明表示的是什么事件,并求出; (2)求的分布列. 解 (1)表示的事件是“恰有次正面朝上”. 因为抛一枚均匀的硬币次,总共有种不同的情况,其中恰有两次正面朝上的情况共有种,所以. (2)根据题意可知,的取值范围是, 又因为用(1)中的方法可知,, 因此的分布列如下表所示.
1分 问题 分析 尝试与发现: 在上一小节中我们已经看到,如果是一个离散型随机变量,都是实数,且,则也是一个离散型随机变量.那么,它们的分布列之间有什么联系? 容易看出,当与都是离散型随机变量而且时,与的分布列如下表所示,它们的第二行的概率值都是一样的. …… ……
…… ……
1分 小结 总结本节课的知识要点,有助于学生落实重点知识与方法。 1、离散型随机变量的分布列 一般地,当离散型随机变量的取值范围是,如果对任意,概率 都是已知的,则称的概率分布是已知的.离散型随机变量的概率分布可以用如下形式的表格表示,这个表格称为的概率分布或分布列. …… ……
2、离散型随机变量的分布列的性质 (1) ; (2) . 3、求离散型随机变量的分布列的步骤 (1)找出随机变量X的所有可能的取值(k=1,2,…,n). (2)求出取每一个值的概率P(X=)=. (3)列出表格.
课后 作业 教材P69练习B 2,4,5 1、B-2 某商店购进一批西瓜,预计晴天西瓜畅销,可获利000元;阴天销路一般,可获利00元;下雨天西瓜滞销,会亏损00元. 根据天气预报,未来数日晴天的概率为.2,下雨的概率为.4,试写出销售这批西瓜获利的分布列. 2、B-4抛一枚均匀的硬币次,设正面朝上的次数为. (1)说明表示的是什么事件,并求出 (2)求的分布列. 3、B-5同时抛两个均匀的骰子,设所得点数之和为 (1)写出的分布列; (2)求; (3)求“点数和大于”的概率.
