4.2.4 随机变量的数字特征(2)教学设计(表格式)
文档属性
| 名称 | 4.2.4 随机变量的数字特征(2)教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 389.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 13:52:04 | ||
图片预览



文档简介
课程基本信息
课题 随机变量的数值特征(2)
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 年 月
教学目标
教学目标: 掌握离散型随机变量的方差与标准差的概念公式,通过梳理初步形成解决离散型随机变量期望与方差的问题的思考步骤; 通过解决离散型随机变量数学期望与方差的实际应用问题,进一步深化离散型随机变量期望与方差的内涵,体会数学的实际应用价值. 教学重点: 如何解决与离散型随机变量的数学期望与方差有关的问题. 教学难点: 如何借助离散型随机变量的数学期望与方差解决生活中的实际问题.
教学过程
时间 教学环节 主要师生活动
5分 复习 回顾, 引入 新课 一般地,设一个离散型随机变量X所有可能取值是 这些值对应的概率是则 叫做这个离散型随机变量X的均值或数学期望; 离散型随机变量X的数学期望刻画了这个离散型随机变量的平均取值水平. 情境与问题:某省要从甲、乙两名射击运动员中选一人参加全运会,根据以往数据,这两名运动员设计幻术的分布列分别如下.若从平均水平和发挥稳定性角度来考虑,要你决定谁参加全运会,你会怎样决定 说明理由. 甲的环数X18910P0.20.60.2
乙的环数X28910P0.40.20.4
因为E(X1)= E(X1)=9,所以仅从平均水平的角度考虑,是无法决定选谁参加的,怎样来衡量他们的发挥稳定性呢? 设甲重复射击足够多次(设为n次)则甲所得环数可以估计为 8,8,…,8,9 ,9,…,9 ,10 ,10,…,10. 甲这组数的方差为 , =0.4 类似的,乙这组数的方差为 =0.8, 由于0.4<0.8,因此可以认为甲的发挥更稳定,应该派甲参加全运会。
5分 新授课 如果离散型随机变量X的分布列如下表所示. Xx1x2…xi…xnPp1p2…pi…pn
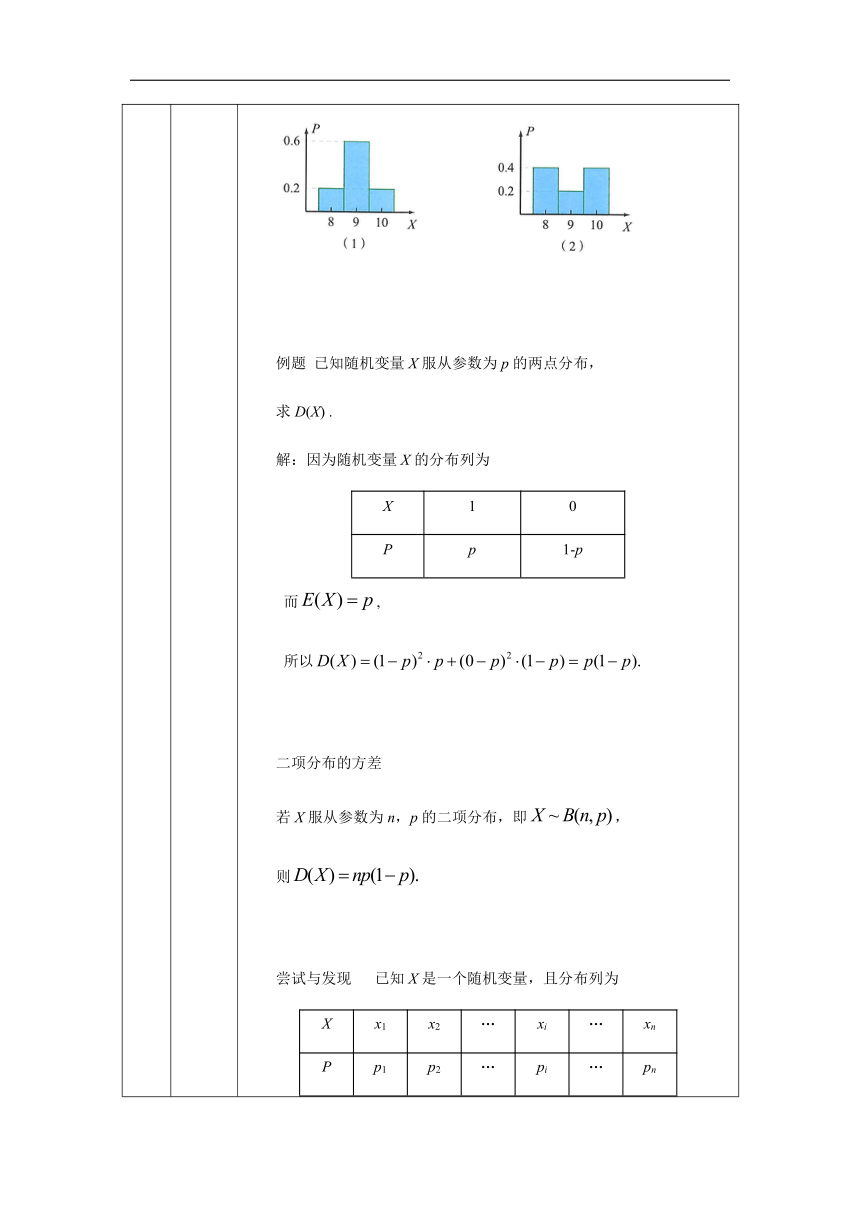
则 叫做这个离散型随机变量X的方差; 称为离散型随机变量X的标准差. 离散型随机变量X的方差和标准差反映了离散型随机变量取值相对于均值的离散程度(或波动大小). 情境与问题中,甲、乙射击环数的分布列用图直观地表示,也能看出D(X 1)与D(X 2)的相对大小. 例题 已知随机变量X服从参数为p的两点分布, 求D(X) . 解:因为随机变量X的分布列为 X10Pp1-p
而, 所以 二项分布的方差 若X服从参数为n,p的二项分布,即, 则 尝试与发现 已知X是一个随机变量,且分布列为 Xx1x2…xi…xnPp1p2…pi…pn
设a,b都是实数。且a≠0,则Y=aX+b也是一个随机变量,而且E(Y)=aE(X)+b,那么,这两个随机变量的方差之间有什么联系呢? 分析:若X与Y都是离散型随机变量,且Y=aX+b,则由X与Y之间分布列和均值之间的关系可知
5分 例题 分析 例题 已知一批产品的次品率为0.02,从这批产品中每次随机取一件,有放回地抽取50次,用X表示抽到的次品数. (1)求D(X); (2)假设抽出的产品需要送往专门的检测部门检测,检测费用Y元与次品数X有关,且Y=10X+300,求D(Y). 解:(1) 因为X服从的是参数为50,0.02的二项分布,即X~B(50,0.02),所以D(X)=50×0.02×(1-0.02)=0.98. (2) D(Y) =D(10X+300)=102D(X) =100×0.98=98.
5分 应用 举例 例题 已知某射击选手射击的命中率是0.8,记他三次独立射击时的命中次数为X,求X的分布列、期望和方差? 解:X的可能取值为0,1,2,3. 所以X的分布列为 X0123P0.0080.0960.3840.512
方法一: 方法二:因为X~B(3,0.8), 所以E(X)=3×0.8=2.4, D(X)=3×0.8×0.2=0.48
2分 例题 分析 例题 A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析, X1和X2的分布列分别为 X12%8%12%X25%10%P0.20.50.3P0.80.2
求:(1)在A、B两个项目上各投资100万元, Y1和Y2分别表示投资项目A和B所获得的利润,求方差D(Y1)和D(Y2); (2)根据得到的结论,对于投资者有什么建议? 解:(1)题目可知,投资项目A和B所获得的利润Y1和Y2的分布列为: Y12812Y2510P0.20.50.3P0.80.2
所以 解:(2) 由(1)可知,说明投资A项目比投资B项目期望收益要高; 同时,说明投资A项目比投资B项目的实际收益相对于期望收益的平均波动要更大. 因此,对于追求稳定的投资者,投资B项目更合适;而对于更看重利润并且愿意为了高利润承担风险的投资者,投资A项目更合适.
1分 课堂 小结 求随机变量的期望与方差的一般步骤(方法一): 找到随机变量X的所有可能取值; 计算X取每一个值xi的概率, 得到X的分布列: Xx1x2…xi…xnPp1p2…pi…pn
2.计算 二项分布:若,,则 , 超几何分布:若离散型随机变量X服从参数为N,M,n的超几何分布,则.
课后 作业 从装有3个白球和2个黑球的布袋中摸取一球,有放回的摸取5次,求摸得的白球数的数学期望和方差. 分析:本题是一道二项分布数学期望与方差的问题. 需要先找到二项分布的重要参数和,再根据公式求解. 解:由题目知摸得的白球数服从参数和的二项分布, 所以, .
课题 随机变量的数值特征(2)
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 年 月
教学目标
教学目标: 掌握离散型随机变量的方差与标准差的概念公式,通过梳理初步形成解决离散型随机变量期望与方差的问题的思考步骤; 通过解决离散型随机变量数学期望与方差的实际应用问题,进一步深化离散型随机变量期望与方差的内涵,体会数学的实际应用价值. 教学重点: 如何解决与离散型随机变量的数学期望与方差有关的问题. 教学难点: 如何借助离散型随机变量的数学期望与方差解决生活中的实际问题.
教学过程
时间 教学环节 主要师生活动
5分 复习 回顾, 引入 新课 一般地,设一个离散型随机变量X所有可能取值是 这些值对应的概率是则 叫做这个离散型随机变量X的均值或数学期望; 离散型随机变量X的数学期望刻画了这个离散型随机变量的平均取值水平. 情境与问题:某省要从甲、乙两名射击运动员中选一人参加全运会,根据以往数据,这两名运动员设计幻术的分布列分别如下.若从平均水平和发挥稳定性角度来考虑,要你决定谁参加全运会,你会怎样决定 说明理由. 甲的环数X18910P0.20.60.2
乙的环数X28910P0.40.20.4
因为E(X1)= E(X1)=9,所以仅从平均水平的角度考虑,是无法决定选谁参加的,怎样来衡量他们的发挥稳定性呢? 设甲重复射击足够多次(设为n次)则甲所得环数可以估计为 8,8,…,8,9 ,9,…,9 ,10 ,10,…,10. 甲这组数的方差为 , =0.4 类似的,乙这组数的方差为 =0.8, 由于0.4<0.8,因此可以认为甲的发挥更稳定,应该派甲参加全运会。
5分 新授课 如果离散型随机变量X的分布列如下表所示. Xx1x2…xi…xnPp1p2…pi…pn
则 叫做这个离散型随机变量X的方差; 称为离散型随机变量X的标准差. 离散型随机变量X的方差和标准差反映了离散型随机变量取值相对于均值的离散程度(或波动大小). 情境与问题中,甲、乙射击环数的分布列用图直观地表示,也能看出D(X 1)与D(X 2)的相对大小. 例题 已知随机变量X服从参数为p的两点分布, 求D(X) . 解:因为随机变量X的分布列为 X10Pp1-p
而, 所以 二项分布的方差 若X服从参数为n,p的二项分布,即, 则 尝试与发现 已知X是一个随机变量,且分布列为 Xx1x2…xi…xnPp1p2…pi…pn
设a,b都是实数。且a≠0,则Y=aX+b也是一个随机变量,而且E(Y)=aE(X)+b,那么,这两个随机变量的方差之间有什么联系呢? 分析:若X与Y都是离散型随机变量,且Y=aX+b,则由X与Y之间分布列和均值之间的关系可知
5分 例题 分析 例题 已知一批产品的次品率为0.02,从这批产品中每次随机取一件,有放回地抽取50次,用X表示抽到的次品数. (1)求D(X); (2)假设抽出的产品需要送往专门的检测部门检测,检测费用Y元与次品数X有关,且Y=10X+300,求D(Y). 解:(1) 因为X服从的是参数为50,0.02的二项分布,即X~B(50,0.02),所以D(X)=50×0.02×(1-0.02)=0.98. (2) D(Y) =D(10X+300)=102D(X) =100×0.98=98.
5分 应用 举例 例题 已知某射击选手射击的命中率是0.8,记他三次独立射击时的命中次数为X,求X的分布列、期望和方差? 解:X的可能取值为0,1,2,3. 所以X的分布列为 X0123P0.0080.0960.3840.512
方法一: 方法二:因为X~B(3,0.8), 所以E(X)=3×0.8=2.4, D(X)=3×0.8×0.2=0.48
2分 例题 分析 例题 A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析, X1和X2的分布列分别为 X12%8%12%X25%10%P0.20.50.3P0.80.2
求:(1)在A、B两个项目上各投资100万元, Y1和Y2分别表示投资项目A和B所获得的利润,求方差D(Y1)和D(Y2); (2)根据得到的结论,对于投资者有什么建议? 解:(1)题目可知,投资项目A和B所获得的利润Y1和Y2的分布列为: Y12812Y2510P0.20.50.3P0.80.2
所以 解:(2) 由(1)可知,说明投资A项目比投资B项目期望收益要高; 同时,说明投资A项目比投资B项目的实际收益相对于期望收益的平均波动要更大. 因此,对于追求稳定的投资者,投资B项目更合适;而对于更看重利润并且愿意为了高利润承担风险的投资者,投资A项目更合适.
1分 课堂 小结 求随机变量的期望与方差的一般步骤(方法一): 找到随机变量X的所有可能取值; 计算X取每一个值xi的概率, 得到X的分布列: Xx1x2…xi…xnPp1p2…pi…pn
2.计算 二项分布:若,,则 , 超几何分布:若离散型随机变量X服从参数为N,M,n的超几何分布,则.
课后 作业 从装有3个白球和2个黑球的布袋中摸取一球,有放回的摸取5次,求摸得的白球数的数学期望和方差. 分析:本题是一道二项分布数学期望与方差的问题. 需要先找到二项分布的重要参数和,再根据公式求解. 解:由题目知摸得的白球数服从参数和的二项分布, 所以, .
