4.2 随机变量小结 教学设计(表格式)
文档属性
| 名称 | 4.2 随机变量小结 教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 105.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 00:00:00 | ||
图片预览



文档简介
课程基本信息
课题 随机变量小结
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 年 月
教学目标
教学目标: 梳理随机变量的知识结构和基本方法,形成系统化的知识结构和方法体系;体会求概率分布列与数学期望、方差的方法;体会超几何分布与二项分布的区别与联系;体验分布模型的建立、分布列的计算和统计图表的数据处理,不断提高数据分析、数学运算等核心素养. 重点:概率分布综合问题的思考策略 难点:分布模型的识别与方法的选择
教学过程
时间 教学环节 主要师生活动
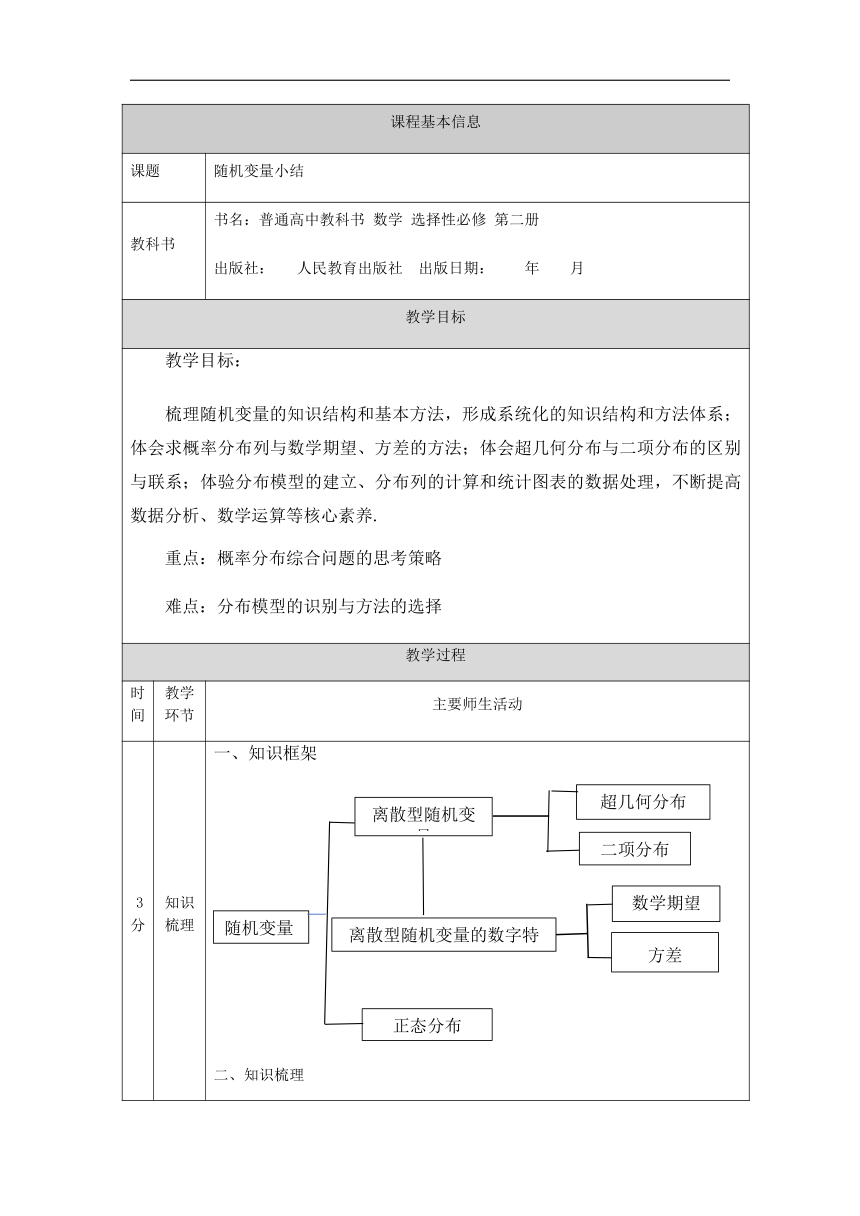
3分 知识梳理 一、知识框架 二、知识梳理 离散型随机变量的分布列: 若P(X=xk)=pk ,k∈{1,2,…,n},则 Xx1x2…xi…xnPp1p2…pi…pn
此表称为X的概率分布或分布列. 求随机变量分布列的步骤 (1)写出随机变量的可能值; (2)求对应概率; (3)列表; (4)检查概率之和是否为1. 几种常见的概率分布 两点分布 X01P1-pp
两点分布又叫伯努利分布,应用非常广泛: 抽取的彩券是否中奖;买回的一件产品是否为正品;新生婴儿的性别;投篮是否命中等. 二项分布:在n次独立重复试验中,事件A在一次试验中发生的概率是p,不发生的概率是1-p ,在这n次独立重复试验中,事件A发生的次数X 服从参数为n,p的二项分布,即X~B(n,p),有 超几何分布:设有总数为N件的甲、乙两类物品,其中甲类有M件(M < N),从所有物品中任取n件(n ≤N),这n 件中所含甲类物品件数X服从参数为N, n, M 的超几何分布,X取不小于t且不大于s的所有自然数,其中s是M和n中的较小者,t在n ≤M –N时取0,否则t=n-(N–M). (二)随机变量的均值 二项分布:若,,则 ; 超几何分布:若离散型随机变量X服从参数为N,M,n的超几何分布,则. (三)随机变量的方差 二项分布:若,,则
5分 例题讲解
设是一个离散型随机变量,其分布列见右表.则等于( ) 分析:根据概率分布列的性质,建立方程求值. 解:由概率分布性质可知:,配方得: 解得:,当时, 与概率性质矛盾,当时,符合题意.选. 小结:概率分列必须满足两个性质:(1);(2), ,所以根据分布列求值,要注意检验.
8分 例题 分析 例 袋中装有 2个白球和 4个黑球,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到黑球时终止,每个球在每一次被取出的机会是等可能的,用X 表示取球终止时所需要的取球次数,求随机变量X 的分布列. 解:由题意得,X的可能取值为 1,2,3. 例 袋中装有 2个白球和 4个黑球,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到黑球时终止,每个球在每一次被取出的机会是等可能的,用X 表示取球终止时所需要的取球次数,求随机变量X 的分布列. 解:由题意得,X的可能取值为 1,2,3.
因此,随机变量X 的分布列为 X123P
例题 某射手每次射击击中目标的概率是0.8,求这名射手在10次射击中, 恰有8次概率; 至少有8次击中目标的概率. (结果保留两个有效数字.) 解:设击中目标的次数为X,则X~B(10,0.8) (1) (2)至少有8次击中目标的概率为 (3)至少应射击几次,才能保证击中目标的概率大于0.99? . 因此,至少应射击3次,才能保证击中目标的概率大于0.99
1分 小结 1. 复习巩固求随机变量分布列、期望、方差的一般方法; 2.进一步学习二项分布与超几何分布的相关知识; 3.关注社会现实生活,感受数学的应用价值.
课后 作业 一条公共汽车线路沿线共有6个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有4位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求: (1)这4位乘客在不相同的车站下车的概率; (2)这4位乘客中恰有2人在终点站下车的概率; (3)设在终点站下车人数为ξ ,求ξ 的分布列和数学期望.
课题 随机变量小结
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 年 月
教学目标
教学目标: 梳理随机变量的知识结构和基本方法,形成系统化的知识结构和方法体系;体会求概率分布列与数学期望、方差的方法;体会超几何分布与二项分布的区别与联系;体验分布模型的建立、分布列的计算和统计图表的数据处理,不断提高数据分析、数学运算等核心素养. 重点:概率分布综合问题的思考策略 难点:分布模型的识别与方法的选择
教学过程
时间 教学环节 主要师生活动
3分 知识梳理 一、知识框架 二、知识梳理 离散型随机变量的分布列: 若P(X=xk)=pk ,k∈{1,2,…,n},则 Xx1x2…xi…xnPp1p2…pi…pn
此表称为X的概率分布或分布列. 求随机变量分布列的步骤 (1)写出随机变量的可能值; (2)求对应概率; (3)列表; (4)检查概率之和是否为1. 几种常见的概率分布 两点分布 X01P1-pp
两点分布又叫伯努利分布,应用非常广泛: 抽取的彩券是否中奖;买回的一件产品是否为正品;新生婴儿的性别;投篮是否命中等. 二项分布:在n次独立重复试验中,事件A在一次试验中发生的概率是p,不发生的概率是1-p ,在这n次独立重复试验中,事件A发生的次数X 服从参数为n,p的二项分布,即X~B(n,p),有 超几何分布:设有总数为N件的甲、乙两类物品,其中甲类有M件(M < N),从所有物品中任取n件(n ≤N),这n 件中所含甲类物品件数X服从参数为N, n, M 的超几何分布,X取不小于t且不大于s的所有自然数,其中s是M和n中的较小者,t在n ≤M –N时取0,否则t=n-(N–M). (二)随机变量的均值 二项分布:若,,则 ; 超几何分布:若离散型随机变量X服从参数为N,M,n的超几何分布,则. (三)随机变量的方差 二项分布:若,,则
5分 例题讲解
设是一个离散型随机变量,其分布列见右表.则等于( ) 分析:根据概率分布列的性质,建立方程求值. 解:由概率分布性质可知:,配方得: 解得:,当时, 与概率性质矛盾,当时,符合题意.选. 小结:概率分列必须满足两个性质:(1);(2), ,所以根据分布列求值,要注意检验.
8分 例题 分析 例 袋中装有 2个白球和 4个黑球,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到黑球时终止,每个球在每一次被取出的机会是等可能的,用X 表示取球终止时所需要的取球次数,求随机变量X 的分布列. 解:由题意得,X的可能取值为 1,2,3. 例 袋中装有 2个白球和 4个黑球,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到黑球时终止,每个球在每一次被取出的机会是等可能的,用X 表示取球终止时所需要的取球次数,求随机变量X 的分布列. 解:由题意得,X的可能取值为 1,2,3.
因此,随机变量X 的分布列为 X123P
例题 某射手每次射击击中目标的概率是0.8,求这名射手在10次射击中, 恰有8次概率; 至少有8次击中目标的概率. (结果保留两个有效数字.) 解:设击中目标的次数为X,则X~B(10,0.8) (1) (2)至少有8次击中目标的概率为 (3)至少应射击几次,才能保证击中目标的概率大于0.99? . 因此,至少应射击3次,才能保证击中目标的概率大于0.99
1分 小结 1. 复习巩固求随机变量分布列、期望、方差的一般方法; 2.进一步学习二项分布与超几何分布的相关知识; 3.关注社会现实生活,感受数学的应用价值.
课后 作业 一条公共汽车线路沿线共有6个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有4位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求: (1)这4位乘客在不相同的车站下车的概率; (2)这4位乘客中恰有2人在终点站下车的概率; (3)设在终点站下车人数为ξ ,求ξ 的分布列和数学期望.
