4.2.5 正态分布 教学设计(表格式)
文档属性
| 名称 | 4.2.5 正态分布 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 978.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 13:52:04 | ||
图片预览

文档简介
课程基本信息
课题 正态分布
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 年 月
教学目标
教学目标: 遵循历史上数学家研究问题的路径,理解正态分布和正态曲线的概念、意义及性质;归纳正态曲线的性质,会用函数的概念、性质解决有关正态分布的问题;挖掘蕴含在其中的数形结合、函数与方程等数学思想方法.通过观察、探究,提高分析问题和解决问题的能力, 教学重点:归纳正态分布曲线的性质特点,掌握3 原则. 教学难点:正态分布的意义的理解和性质的应用.
教学过程
时间 教学环节 主要师生活动
3分 新课 引入 尝试与发现 已知X服从参数为100,0.5的二项分布,即X~B(100,0.5),你能手工计算出P(X=50)的值吗? 因为,手工计算该值是一个“几乎不可能”完成的任务,由此可以看出,若X~B(n,p),那么n较大时,直接计算P(X=k)的值将是十分困难的,有没有其他办法能得到上式的近似值呢? 例如,若X~B(6,),则X的分布列如下. X0123456P
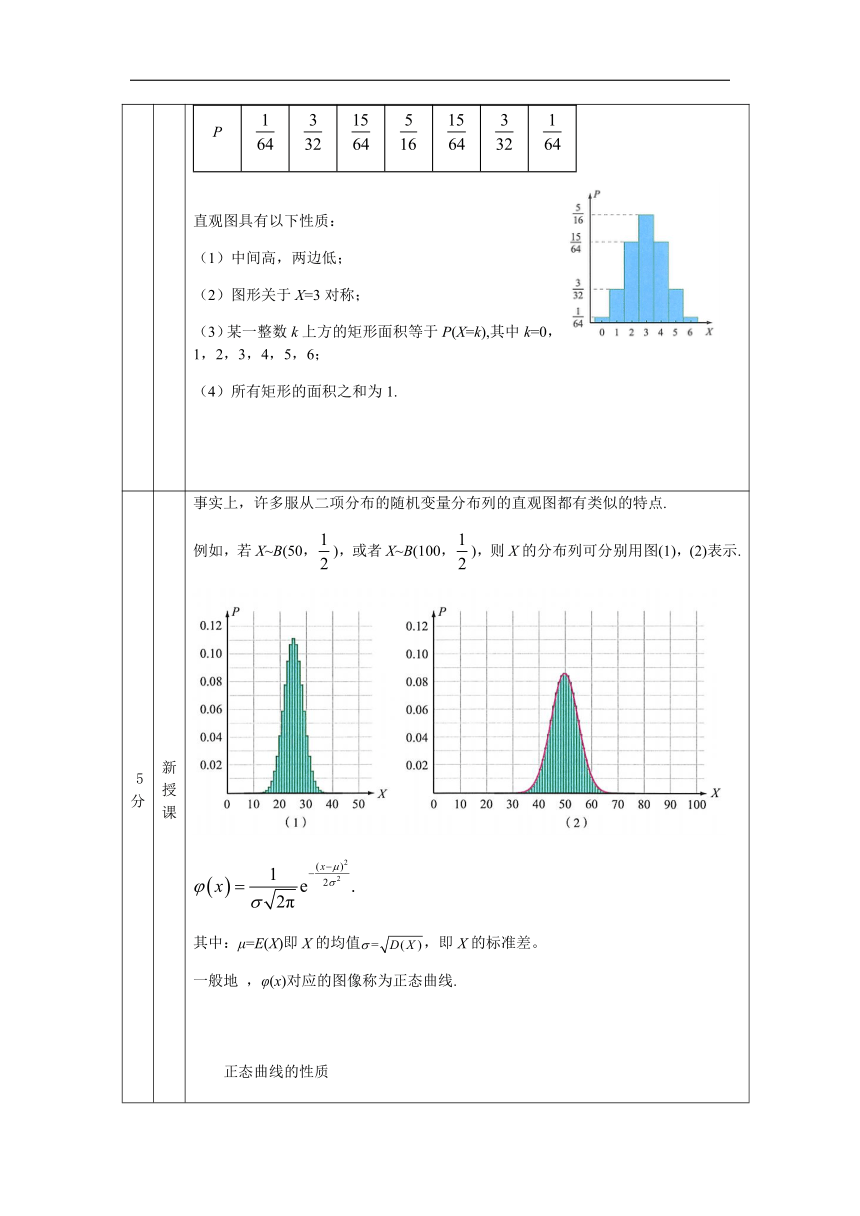
直观图具有以下性质: (1)中间高,两边低; (2)图形关于X=3对称; (3)某一整数k上方的矩形面积等于P(X=k),其中k=0,1,2,3,4,5,6; (4)所有矩形的面积之和为1.
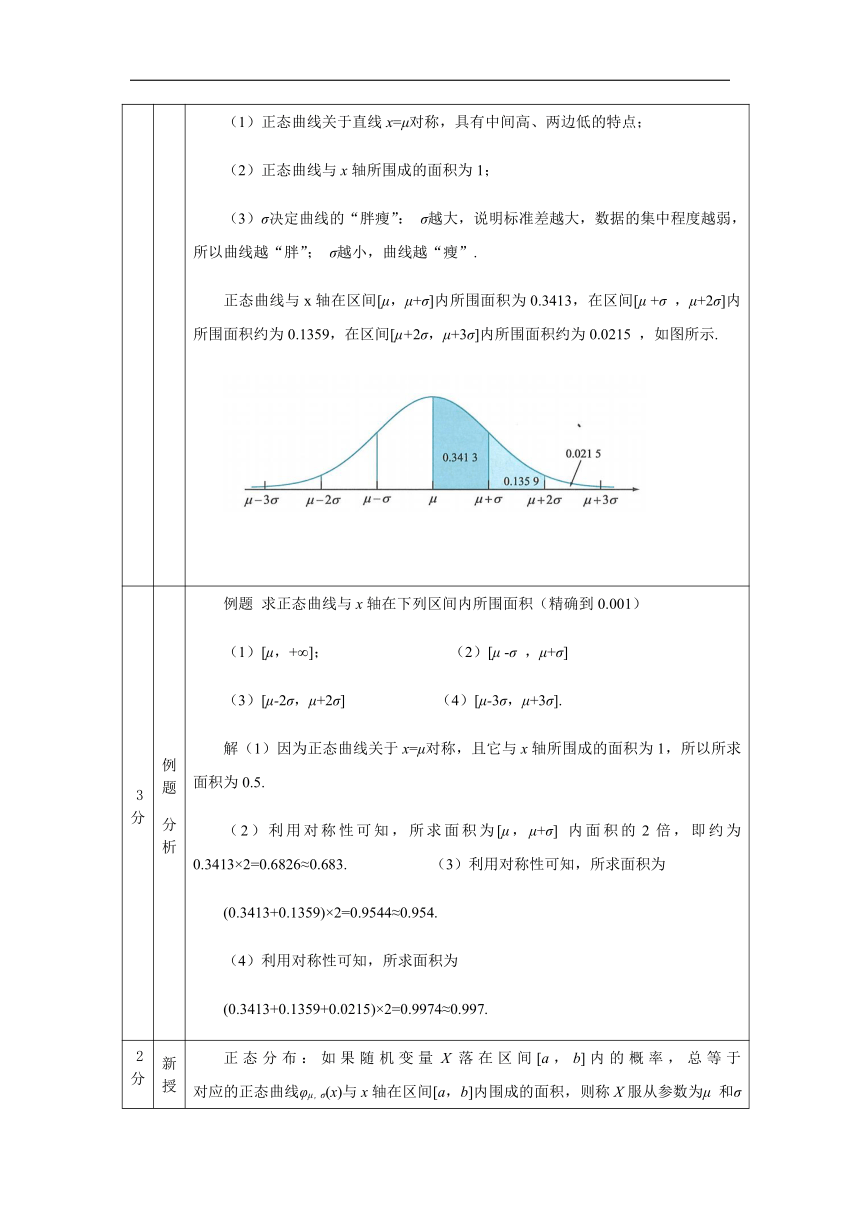
5分 新授课 事实上,许多服从二项分布的随机变量分布列的直观图都有类似的特点. 例如,若X~B(50,),或者X~B(100,),则X的分布列可分别用图(1),(2)表示. 其中:μ=E(X)即X的均值,即X的标准差。 一般地 ,φ(x)对应的图像称为正态曲线. 正态曲线的性质 (1)正态曲线关于直线x=μ对称,具有中间高、两边低的特点; (2)正态曲线与x轴所围成的面积为1; (3)σ决定曲线的“胖瘦”: σ越大,说明标准差越大,数据的集中程度越弱,所以曲线越“胖”; σ越小,曲线越“瘦”. 正态曲线与x轴在区间[μ,μ+σ]内所围面积为0.3413,在区间[μ +σ ,μ+2σ]内所围面积约为0.1359,在区间[μ+2σ,μ+3σ]内所围面积约为0.0215 ,如图所示.
3分 例题 分析 例题 求正态曲线与x轴在下列区间内所围面积(精确到0.001) (1)[μ,+∞]; (2)[μ -σ ,μ+σ] (3)[μ-2σ,μ+2σ] (4)[μ-3σ,μ+3σ]. 解(1)因为正态曲线关于x=μ对称,且它与x轴所围成的面积为1,所以所求面积为0.5. (2)利用对称性可知,所求面积为[μ,μ+σ] 内面积的2倍,即约为0.3413×2=0.6826≈0.683. (3)利用对称性可知,所求面积为 (0.3413+0.1359)×2=0.9544≈0.954. (4)利用对称性可知,所求面积为 (0.3413+0.1359+0.0215)×2=0.9974≈0.997.
2分 新授课 正态分布:如果随机变量X落在区间[a,b]内的概率,总等于 对应的正态曲线φμ,σ(x)与x轴在区间[a,b]内围成的面积,则称X服从参数为μ 和σ的正态分布,记作X~N(μ ,σ2 ). μ是X的平均值, σ是X的标准差,σ2是X的方差. 由正态曲线的性质及前面例题可知,如果X~N(μ ,σ2 ),那么 P(X≤μ )= P(X≥μ )=0.5, P(|X –μ|≤σ)= P(μ-σ≤X≤μ+σ ) ≈68.3%, P(|X –μ|≤2σ)= P(μ-2σ≤X≤μ+2σ ) ≈95.4%, P(|X –μ|≤3σ)= P(μ- 3σ≤X≤μ+ 3σ ) ≈99.7%. 现实生活中,很多随机变量都服从或近似服从正态分布:随机误差、同一地区同龄人的身高、正常条件下生产出来的产品尺寸、同一批灯泡的寿命等.
3分 例题 分析 例 假设某地区高二学生的身高服从正态分布,且均值为170(单位:cm,下同),标准差为10.在该地区任意抽取一名高二学生,求这名学生的身高: (1)不高于170的概率; (2)在区间[160,180]内的概率; (3)不高于180的概率. 解:设该学生的身高为X,由题意可知X~N(170 ,102 ). (1)P(X≤170 )=50%, (2)因为均值为170,标准差为10,而160=170-10,180=170+10,所以 P(160≤X≤ 170 ) =P(|X –170|≤10) ≈68.3%, (3)由(2)以及正态曲线的对称性可知 P(170≤X≤ 180 )= P(160≤X≤ 180 ) ≈ 68.3%=34.15%, 由概率加法公式可知P(X≤ 180 )= P(X≤ 170 )+ P(170≤X≤ 180 ) ≈ 50%+34.15%=84.15%.
2分 标准正态分布:μ =0,σ=1的正态分布称为标准正态分布,记作X~N(0 ,1 ),对于任意a,通常记Φ(a)=P(X3分 例 已知X~N(0 ,1 ),利用上述表格求以下概率值:(1)P(X < 0.28);(2)P(X <- 0.36); (3)P(0.18≤X < 0.57); 解:(1)P(X < 0.28)= Φ(a)= 0.6103; (2)P(X < -0.36)=Φ(-0.36)=1-Φ(0.36)=0.3594 (3)P(0.18≤X < 0.57)= P(X < 0.57) -P(X <0.18 )= Φ(0.57) -Φ(0.18) =0.1443.
1分 小结 1.二项分布与正态曲线,曲线的性质与特点; 2.正态分布与3 原则; 3.标准正态分布.
课后 作业 设,则落在内的概率是( ) A.95.44% B.99.74% C.4.56% D.0.26% 解析:由知,=-2, =12,则==0.9974.
课题 正态分布
教科书 书名:普通高中教科书 数学 选择性必修 第二册 出版社: 人民教育出版社 出版日期: 年 月
教学目标
教学目标: 遵循历史上数学家研究问题的路径,理解正态分布和正态曲线的概念、意义及性质;归纳正态曲线的性质,会用函数的概念、性质解决有关正态分布的问题;挖掘蕴含在其中的数形结合、函数与方程等数学思想方法.通过观察、探究,提高分析问题和解决问题的能力, 教学重点:归纳正态分布曲线的性质特点,掌握3 原则. 教学难点:正态分布的意义的理解和性质的应用.
教学过程
时间 教学环节 主要师生活动
3分 新课 引入 尝试与发现 已知X服从参数为100,0.5的二项分布,即X~B(100,0.5),你能手工计算出P(X=50)的值吗? 因为,手工计算该值是一个“几乎不可能”完成的任务,由此可以看出,若X~B(n,p),那么n较大时,直接计算P(X=k)的值将是十分困难的,有没有其他办法能得到上式的近似值呢? 例如,若X~B(6,),则X的分布列如下. X0123456P
直观图具有以下性质: (1)中间高,两边低; (2)图形关于X=3对称; (3)某一整数k上方的矩形面积等于P(X=k),其中k=0,1,2,3,4,5,6; (4)所有矩形的面积之和为1.
5分 新授课 事实上,许多服从二项分布的随机变量分布列的直观图都有类似的特点. 例如,若X~B(50,),或者X~B(100,),则X的分布列可分别用图(1),(2)表示. 其中:μ=E(X)即X的均值,即X的标准差。 一般地 ,φ(x)对应的图像称为正态曲线. 正态曲线的性质 (1)正态曲线关于直线x=μ对称,具有中间高、两边低的特点; (2)正态曲线与x轴所围成的面积为1; (3)σ决定曲线的“胖瘦”: σ越大,说明标准差越大,数据的集中程度越弱,所以曲线越“胖”; σ越小,曲线越“瘦”. 正态曲线与x轴在区间[μ,μ+σ]内所围面积为0.3413,在区间[μ +σ ,μ+2σ]内所围面积约为0.1359,在区间[μ+2σ,μ+3σ]内所围面积约为0.0215 ,如图所示.
3分 例题 分析 例题 求正态曲线与x轴在下列区间内所围面积(精确到0.001) (1)[μ,+∞]; (2)[μ -σ ,μ+σ] (3)[μ-2σ,μ+2σ] (4)[μ-3σ,μ+3σ]. 解(1)因为正态曲线关于x=μ对称,且它与x轴所围成的面积为1,所以所求面积为0.5. (2)利用对称性可知,所求面积为[μ,μ+σ] 内面积的2倍,即约为0.3413×2=0.6826≈0.683. (3)利用对称性可知,所求面积为 (0.3413+0.1359)×2=0.9544≈0.954. (4)利用对称性可知,所求面积为 (0.3413+0.1359+0.0215)×2=0.9974≈0.997.
2分 新授课 正态分布:如果随机变量X落在区间[a,b]内的概率,总等于 对应的正态曲线φμ,σ(x)与x轴在区间[a,b]内围成的面积,则称X服从参数为μ 和σ的正态分布,记作X~N(μ ,σ2 ). μ是X的平均值, σ是X的标准差,σ2是X的方差. 由正态曲线的性质及前面例题可知,如果X~N(μ ,σ2 ),那么 P(X≤μ )= P(X≥μ )=0.5, P(|X –μ|≤σ)= P(μ-σ≤X≤μ+σ ) ≈68.3%, P(|X –μ|≤2σ)= P(μ-2σ≤X≤μ+2σ ) ≈95.4%, P(|X –μ|≤3σ)= P(μ- 3σ≤X≤μ+ 3σ ) ≈99.7%. 现实生活中,很多随机变量都服从或近似服从正态分布:随机误差、同一地区同龄人的身高、正常条件下生产出来的产品尺寸、同一批灯泡的寿命等.
3分 例题 分析 例 假设某地区高二学生的身高服从正态分布,且均值为170(单位:cm,下同),标准差为10.在该地区任意抽取一名高二学生,求这名学生的身高: (1)不高于170的概率; (2)在区间[160,180]内的概率; (3)不高于180的概率. 解:设该学生的身高为X,由题意可知X~N(170 ,102 ). (1)P(X≤170 )=50%, (2)因为均值为170,标准差为10,而160=170-10,180=170+10,所以 P(160≤X≤ 170 ) =P(|X –170|≤10) ≈68.3%, (3)由(2)以及正态曲线的对称性可知 P(170≤X≤ 180 )= P(160≤X≤ 180 ) ≈ 68.3%=34.15%, 由概率加法公式可知P(X≤ 180 )= P(X≤ 170 )+ P(170≤X≤ 180 ) ≈ 50%+34.15%=84.15%.
2分 标准正态分布:μ =0,σ=1的正态分布称为标准正态分布,记作X~N(0 ,1 ),对于任意a,通常记Φ(a)=P(X
1分 小结 1.二项分布与正态曲线,曲线的性质与特点; 2.正态分布与3 原则; 3.标准正态分布.
课后 作业 设,则落在内的概率是( ) A.95.44% B.99.74% C.4.56% D.0.26% 解析:由知,=-2, =12,则==0.9974.
