2022-2023学年高一数学同步备课系列(人教A版2019必修第一册)3.3 幂函数(教学课件)(37张ppt)
文档属性
| 名称 | 2022-2023学年高一数学同步备课系列(人教A版2019必修第一册)3.3 幂函数(教学课件)(37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 15:05:00 | ||
图片预览










文档简介
3.3 幂函数
第 3章 函数的概念与性质
人教A版2019必修第一册
01幂函数的概念
02幂函数的图像和性质
目录
03幂函数的单调性
04.利用幂函数的单调性比较
指数幂的大小
3
学习目标
1、理解幂函数的概念,会画幂函数
y=x,y=x2,y=x3,y=x-1,y=x 的图象;
2、结合这几个幂函数的图象,理解幂函数图象的变化情况和性质;
3、通过观察、总结幂函数的性质,培养学生概括抽象和识图能力.
4
重点难点
重点:
常见幂函数的概念、图象和性质
难点:
幂函数的单调性及比较两个幂值的大小
第一次给幂这个概念下定义的是我国明代著名的科学家、政治家徐光启,同时他还是一位沟通中西文化的先行者。徐光启在和意大利人利玛窦合译欧几里德《几何原本》时,给幂字下注解:“自乘之数曰幂”。
徐光启
(1562—1633)
情景引入
前面学习了函数的概念,利用函数概念和对函数的观察,研究了函数的一些性质.本节我们利用这些知识研究一类新的函数.先看几个实例.
(1)如果宋老师以1元/????????的价格购买了某种蔬菜????????????,那么她需要支付????=????元,这里????是????的函数;
(2)如果正方形的边长为????,那么正方形的面积????=????2,这里????是????的函数;
(3)如果立方体的棱长为????,那么立方体的体积????=????3,这里????是????的函数;
(4)如果一个正方形场地的面积为????,那么这个正方形场地的边长????=????,这里????是????的函数;
(5)如果某人?????????内骑车行进了1????????,那么他骑车的平均速度????=1????????????/????,即????=?????1,这里????是????的函数.
?
(1)????=????; (2)????=????2; (3)????=????3;
(4)????=????,即????=????12; (5)????=1????,即????=?????1.
?
活动1:请观察(1)—(5)中的函数解析式,讨论它们有何共同特征.
实际上,这些函数的解析式都有幂的形式,而且都是以幂的底数为自变量;幂的指数都是常数,分别是1,2,3,????????,-1;它们都是形如????=????????的函数.
?
一般地,函数????=????????叫做幂函数,其中是自变量,是常数.
?
注:幂函数中????的系数为“1”.
?
1.在函数????=1????2,????=2????2,????=????3+????,????=1中,幂函数的个数为( ).
????.0?????????????????????????????????.1???????????????????????????????????.2??????????????????????????????????????.3
?
答案:B.其中????=1的定义域为R,而????=????0中,????≠0.所以????=1不是幂函数.
?
练一练
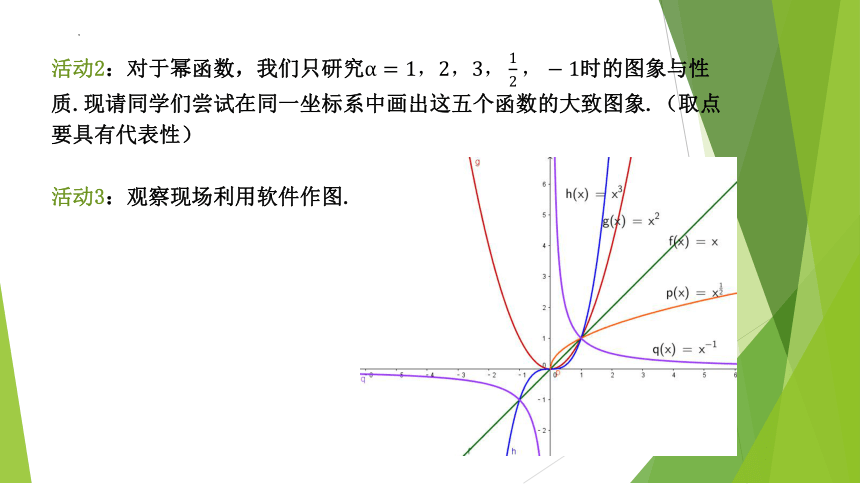
活动2:对于幂函数,我们只研究α=1,2,3,12,?1时的图象与性质.现请同学们尝试在同一坐标系中画出这五个函数的大致图象.(取点要具有代表性)
活动3:观察现场利用软件作图.
?
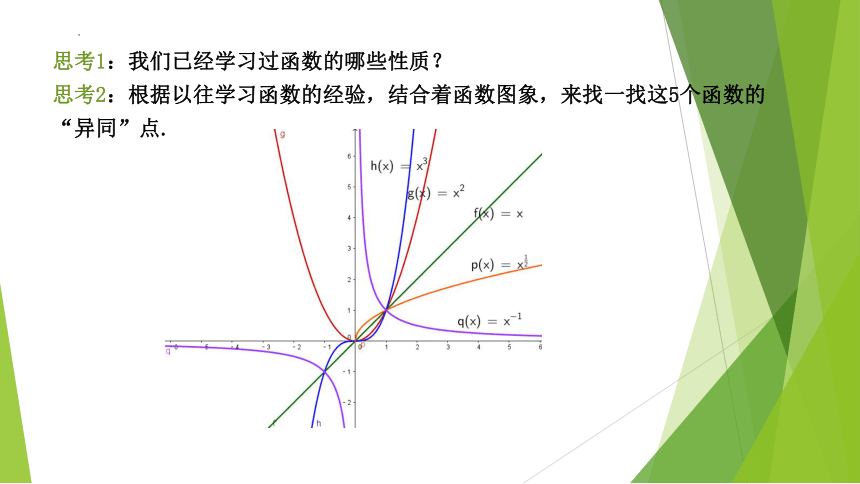
思考1:我们已经学习过函数的哪些性质?
思考2:根据以往学习函数的经验,结合着函数图象,来找一找这5个函数的“异同”点.
思考3:观察5个函数图象,哪个象限一定有幂函数的图象,哪个象限一定没有
幂函数的图象.
幂函数????=????????的性质:
(1)过定点(1,1);
(2)幂函数的图象一定会在第一象限,一定不在第四象限;
(3)当????>0时,函数在区间[0,+∞)上是增函数;
(4)当????<0时,函数在区间[0,+∞)上是减函数;
(5)在(0,1)上,指数越大,幂函数图象越靠近????轴(指大图低);
(6)在(1,+∞)上,指数越大,幂函数图象越远离????轴(指大图高);
?
2.判断正误.
(1)幂函数的图象必过(0,0)和(1,1).( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)当幂指数????取1,3,????????时,幂函数????=????????是增函数.( )
(4)若幂函数????=????????的图象关于原点对称,则????=????????在定义域内
????随????的增大而增大.( )
?
答案:×,×,√,×.
练一练
1.幂函数的概念
已知函数 ,m为何值时,f(x)是幂函数?
解:若f(x)为幂函数,则m2+2m -2=1,∴m=-3或1.
3.函数 是幂函数,且在(0,+∞)上是减函数,求实数m的值。
解:由m2-m+1=1,得m=0或m=1,再把m=0和m=1分别代入m2+2m-3<0检验,得m=0
典例1
练一练
4.已知幂函数 的图像经过点 ,求这个函数的表达式.
????=????????
?
????,????
?
【解】由题意设函数的表达式为
????????=????????
?
把点 代入,得:
????,????
?
????=????????
?
即 ,所以
????????????=????????
?
????=????????
?
所以这个函数的表达式为
????????=????????????
?
和初中解决一次函数一样,利用待定系数法.因为幂函数只有一个系数,所以只需要一个点的坐标就可以求写出幂函数的表达式.
练一练
2.幂函数的图像与性质
n典例2
[解析] 过原点的指数α>0,不过原点的α<0,
∴n<0,
当x>1时,在直线y=x上方的α>1,下方的α<1,
∴p>1,0x>1时,指数越大,图象越高,∴m>q,
综上所述n[答案] n求幂函数 的定义域并讨论其奇偶性和单调性.
【解】因为 , ,又 为
两个连续的正整数相乘,其结果必为正偶数,所以
为正奇数,所以函数的定义域为R.
????????=????????????????+????+????????∈?????
?
????????+????+????=????????+????+????
?
????∈?????
?
????????+????
?
????????+????+????
?
由 为正奇数,得
????????+????+????
?
?????????=?????????????????+????+????=?????????????????+????+????=?????????
?
,所以 为增函数.
????????
?
因为 ,所以 是正的奇次方根,所以
在定义域内为增函数.
????????????+????+????>????
?
????????????????+????+????
?
????????
?
典例3
3.幂函数的单调性
【例题】证明幂函数 是增函数.
????????=????
?
【证明】函数的定义域是[0,+∞).
?????????,????????∈????,+∞,且?????????
?????????????????????????=?????????????????
?
=?????????????????????????+????????????????+????????
?
=??????????????????????????+????????
?
因为 , ,所以
??????????????????
????????+????????>????
?
?????????????
即幂函数 是增函数.
????????=????
?
典例4
练一练
4.利用幂函数的单调性
比较指数幂的大小
利用幂函数的性质,比较下列两个数的大小.
【解】设 ,则 在R上为增函数.
比较大小用作差法.由增减性,根据自变量的大小,比较函数值的大小;或者根据函数值的大小,比较自变量的大小.
????????=????????
?
????????
?
∵ -1.5<-1.4,∴ (-1.5)3<(-1.4)3
(-1.5)3 和 (-1.4)3
典例5
课堂练习
2.若f(x)=(m2-4m+5)x-m+|n+1|是幂函数,则f(2)=_____.
不是
1.辨析1:判断下列函数是不是幂函数?
是
不是
不是
是
不是
由f(x)=(m2-4m+5)x-m+|n+1|是幂函数得
∴f(x)=x-2,
简析:
3.判断正误.
(1)幂函数的图象必过(0,0)和(1,1).( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)当幂指数????取1,3,????????时,幂函数????=????????是增函数.( )
(4)若幂函数????=????????的图象关于原点对称,则????=????????在定义域内????随????的增大而增大.( )
?
×
×
√
×
4.若四个幂函数图象????=????????,????=????????,????=????????,????=????????在同一坐标系中的图象如图所示,则????,????,????,????的大小关系是( ).
????.????>????>????>????????????????.????>????>????>????????????????.????>????>????>????????????????.????>????>????>????
?
????=????????
?
????=????????
?
????=????????
?
????=????????
?
随堂检测
1.已知幂函数的图像经过点(9,3),求这个幂函数的解析式.
设幂函数为 ????????=????????,
?
因为图像经过点(9,3),
所以 3=9?????,
?
所以 ????????=???????????? .
?
所以 ????=????????,
?
2.比较下面两组数的大小.
(1) 2.31.1 和 2.51.1 (2)(????2+2)????????? 和 2?????????
?
3.如果幂函数的图象????=(?????????????????+????)??????????????????????不过原点,求实数m的值
?
4.在同一平面直角坐标系中画出函数 ????????=???? 与 ????????=?????1 的图象,并利用图象求不等式 ????> ?????1 的解集.
?
5.已知在区间(0,?????)(????<0)上,函数????=????????2?1与????=????????2+????????+12????+1都是减函数,试求????的取值范围.
?
6.下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.
6.下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.
第 3章 函数的概念与性质
人教A版2019必修第一册
01幂函数的概念
02幂函数的图像和性质
目录
03幂函数的单调性
04.利用幂函数的单调性比较
指数幂的大小
3
学习目标
1、理解幂函数的概念,会画幂函数
y=x,y=x2,y=x3,y=x-1,y=x 的图象;
2、结合这几个幂函数的图象,理解幂函数图象的变化情况和性质;
3、通过观察、总结幂函数的性质,培养学生概括抽象和识图能力.
4
重点难点
重点:
常见幂函数的概念、图象和性质
难点:
幂函数的单调性及比较两个幂值的大小
第一次给幂这个概念下定义的是我国明代著名的科学家、政治家徐光启,同时他还是一位沟通中西文化的先行者。徐光启在和意大利人利玛窦合译欧几里德《几何原本》时,给幂字下注解:“自乘之数曰幂”。
徐光启
(1562—1633)
情景引入
前面学习了函数的概念,利用函数概念和对函数的观察,研究了函数的一些性质.本节我们利用这些知识研究一类新的函数.先看几个实例.
(1)如果宋老师以1元/????????的价格购买了某种蔬菜????????????,那么她需要支付????=????元,这里????是????的函数;
(2)如果正方形的边长为????,那么正方形的面积????=????2,这里????是????的函数;
(3)如果立方体的棱长为????,那么立方体的体积????=????3,这里????是????的函数;
(4)如果一个正方形场地的面积为????,那么这个正方形场地的边长????=????,这里????是????的函数;
(5)如果某人?????????内骑车行进了1????????,那么他骑车的平均速度????=1????????????/????,即????=?????1,这里????是????的函数.
?
(1)????=????; (2)????=????2; (3)????=????3;
(4)????=????,即????=????12; (5)????=1????,即????=?????1.
?
活动1:请观察(1)—(5)中的函数解析式,讨论它们有何共同特征.
实际上,这些函数的解析式都有幂的形式,而且都是以幂的底数为自变量;幂的指数都是常数,分别是1,2,3,????????,-1;它们都是形如????=????????的函数.
?
一般地,函数????=????????叫做幂函数,其中是自变量,是常数.
?
注:幂函数中????的系数为“1”.
?
1.在函数????=1????2,????=2????2,????=????3+????,????=1中,幂函数的个数为( ).
????.0?????????????????????????????????.1???????????????????????????????????.2??????????????????????????????????????.3
?
答案:B.其中????=1的定义域为R,而????=????0中,????≠0.所以????=1不是幂函数.
?
练一练
活动2:对于幂函数,我们只研究α=1,2,3,12,?1时的图象与性质.现请同学们尝试在同一坐标系中画出这五个函数的大致图象.(取点要具有代表性)
活动3:观察现场利用软件作图.
?
思考1:我们已经学习过函数的哪些性质?
思考2:根据以往学习函数的经验,结合着函数图象,来找一找这5个函数的“异同”点.
思考3:观察5个函数图象,哪个象限一定有幂函数的图象,哪个象限一定没有
幂函数的图象.
幂函数????=????????的性质:
(1)过定点(1,1);
(2)幂函数的图象一定会在第一象限,一定不在第四象限;
(3)当????>0时,函数在区间[0,+∞)上是增函数;
(4)当????<0时,函数在区间[0,+∞)上是减函数;
(5)在(0,1)上,指数越大,幂函数图象越靠近????轴(指大图低);
(6)在(1,+∞)上,指数越大,幂函数图象越远离????轴(指大图高);
?
2.判断正误.
(1)幂函数的图象必过(0,0)和(1,1).( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)当幂指数????取1,3,????????时,幂函数????=????????是增函数.( )
(4)若幂函数????=????????的图象关于原点对称,则????=????????在定义域内
????随????的增大而增大.( )
?
答案:×,×,√,×.
练一练
1.幂函数的概念
已知函数 ,m为何值时,f(x)是幂函数?
解:若f(x)为幂函数,则m2+2m -2=1,∴m=-3或1.
3.函数 是幂函数,且在(0,+∞)上是减函数,求实数m的值。
解:由m2-m+1=1,得m=0或m=1,再把m=0和m=1分别代入m2+2m-3<0检验,得m=0
典例1
练一练
4.已知幂函数 的图像经过点 ,求这个函数的表达式.
????=????????
?
????,????
?
【解】由题意设函数的表达式为
????????=????????
?
把点 代入,得:
????,????
?
????=????????
?
即 ,所以
????????????=????????
?
????=????????
?
所以这个函数的表达式为
????????=????????????
?
和初中解决一次函数一样,利用待定系数法.因为幂函数只有一个系数,所以只需要一个点的坐标就可以求写出幂函数的表达式.
练一练
2.幂函数的图像与性质
n
[解析] 过原点的指数α>0,不过原点的α<0,
∴n<0,
当x>1时,在直线y=x上方的α>1,下方的α<1,
∴p>1,0
综上所述n
【解】因为 , ,又 为
两个连续的正整数相乘,其结果必为正偶数,所以
为正奇数,所以函数的定义域为R.
????????=????????????????+????+????????∈?????
?
????????+????+????=????????+????+????
?
????∈?????
?
????????+????
?
????????+????+????
?
由 为正奇数,得
????????+????+????
?
?????????=?????????????????+????+????=?????????????????+????+????=?????????
?
,所以 为增函数.
????????
?
因为 ,所以 是正的奇次方根,所以
在定义域内为增函数.
????????????+????+????>????
?
????????????????+????+????
?
????????
?
典例3
3.幂函数的单调性
【例题】证明幂函数 是增函数.
????????=????
?
【证明】函数的定义域是[0,+∞).
?????????,????????∈????,+∞,且?????????
?????????????????????????=?????????????????
?
=?????????????????????????+????????????????+????????
?
=??????????????????????????+????????
?
因为 , ,所以
??????????????????
????????+????????>????
?
?????????????
即幂函数 是增函数.
????????=????
?
典例4
练一练
4.利用幂函数的单调性
比较指数幂的大小
利用幂函数的性质,比较下列两个数的大小.
【解】设 ,则 在R上为增函数.
比较大小用作差法.由增减性,根据自变量的大小,比较函数值的大小;或者根据函数值的大小,比较自变量的大小.
????????=????????
?
????????
?
∵ -1.5<-1.4,∴ (-1.5)3<(-1.4)3
(-1.5)3 和 (-1.4)3
典例5
课堂练习
2.若f(x)=(m2-4m+5)x-m+|n+1|是幂函数,则f(2)=_____.
不是
1.辨析1:判断下列函数是不是幂函数?
是
不是
不是
是
不是
由f(x)=(m2-4m+5)x-m+|n+1|是幂函数得
∴f(x)=x-2,
简析:
3.判断正误.
(1)幂函数的图象必过(0,0)和(1,1).( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)当幂指数????取1,3,????????时,幂函数????=????????是增函数.( )
(4)若幂函数????=????????的图象关于原点对称,则????=????????在定义域内????随????的增大而增大.( )
?
×
×
√
×
4.若四个幂函数图象????=????????,????=????????,????=????????,????=????????在同一坐标系中的图象如图所示,则????,????,????,????的大小关系是( ).
????.????>????>????>????????????????.????>????>????>????????????????.????>????>????>????????????????.????>????>????>????
?
????=????????
?
????=????????
?
????=????????
?
????=????????
?
随堂检测
1.已知幂函数的图像经过点(9,3),求这个幂函数的解析式.
设幂函数为 ????????=????????,
?
因为图像经过点(9,3),
所以 3=9?????,
?
所以 ????????=???????????? .
?
所以 ????=????????,
?
2.比较下面两组数的大小.
(1) 2.31.1 和 2.51.1 (2)(????2+2)????????? 和 2?????????
?
3.如果幂函数的图象????=(?????????????????+????)??????????????????????不过原点,求实数m的值
?
4.在同一平面直角坐标系中画出函数 ????????=???? 与 ????????=?????1 的图象,并利用图象求不等式 ????> ?????1 的解集.
?
5.已知在区间(0,?????)(????<0)上,函数????=????????2?1与????=????????2+????????+12????+1都是减函数,试求????的取值范围.
?
6.下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.
6.下面六个幂函数的图象如图所示,试建立函数与图象之间的对应关系.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
