2022—2023学年九年级人教版数学上册24.1.2 垂直于弦的直径 课时练习(含解析)
文档属性
| 名称 | 2022—2023学年九年级人教版数学上册24.1.2 垂直于弦的直径 课时练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 928.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 00:00:00 | ||
图片预览


文档简介
24.1.2 垂直于弦的直径(附解析)
一、单选题(共10个小题)
1.如图,AB为⊙O的弦,半径OC⊥AB于点D ,且AB=6,OD=4,则DC的长为( )
A.1 B.2 C.2.5 D.5
2.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.(4﹣)米 B.2米 C.3米 D.(4+)米
3.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1或7 B.7 C.1 D.3或4
4.如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于C点,AB=12cm,AO=8cm,则OC长为( )cm
A.5 B.4 C. D.
5.如图,⊙O的半径为10,弦AB=16,M是弦AB上的动点,则OM不可能为( )
A.5 B.6 C.7 D.8
6.下列说法正确的是( )
①平分弧的直径垂直平分弧所对的弦
②平分弦的直径平分弦所对的弧
③垂直于弦的直线必过圆心
④垂直于弦的直径平分弦所对的弧
A.②③ B.①③ C.②④ D.①④
7.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
8.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为( )
A.22寸 B.24寸 C.26寸 D.28寸
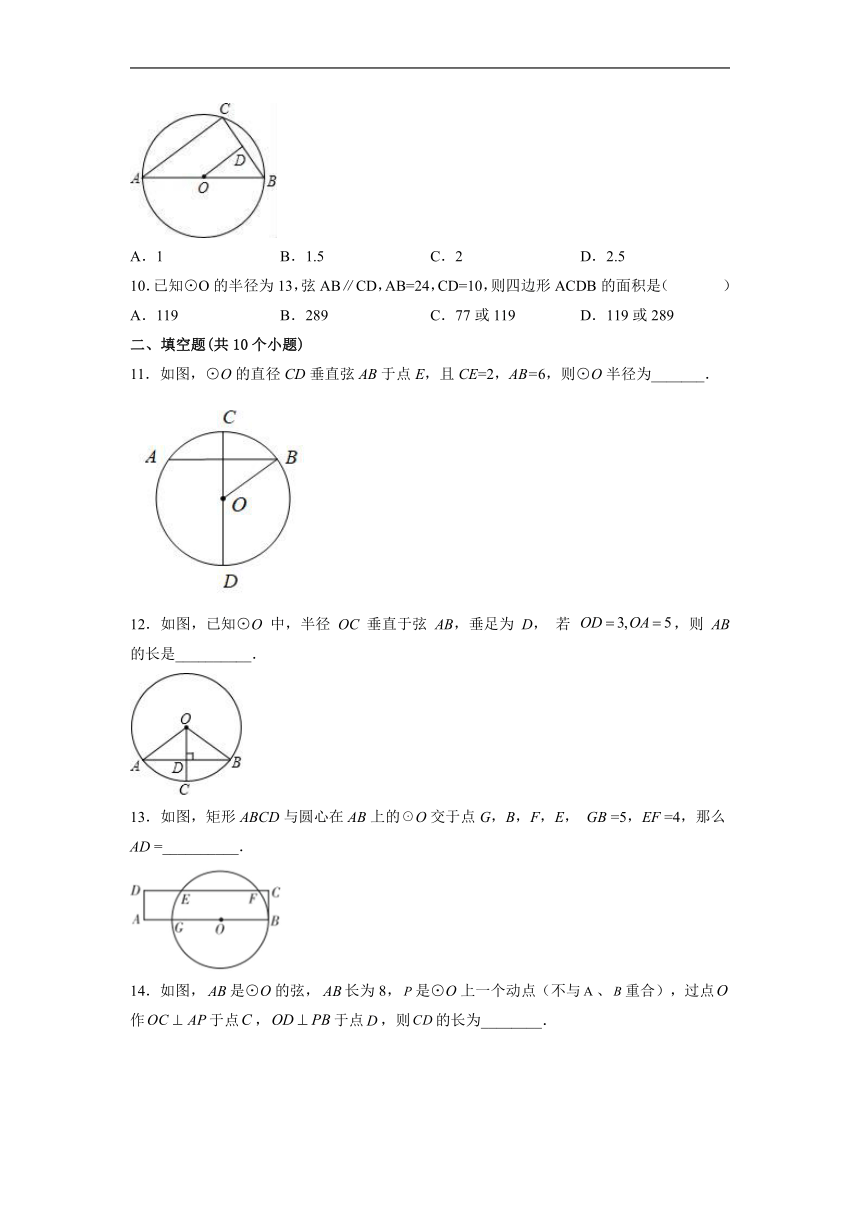
9.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
A.1 B.1.5 C.2 D.2.5
10.已知⊙O的半径为13,弦AB∥CD,AB=24,CD=10,则四边形ACDB的面积是( )
A.119 B.289 C.77或119 D.119或289
二、填空题(共10个小题)
11.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=6,则⊙O半径为_______.
12.如图,已知⊙O 中,半径 OC 垂直于弦 AB,垂足为 D, 若 ,则 AB 的长是__________.
13.如图,矩形ABCD与圆心在AB上的☉O交于点G,B,F,E, GB =5,EF =4,那么AD =__________.
14.如图,是⊙O的弦,长为8,是⊙O上一个动点(不与、重合),过点作于点,于点,则的长为________.
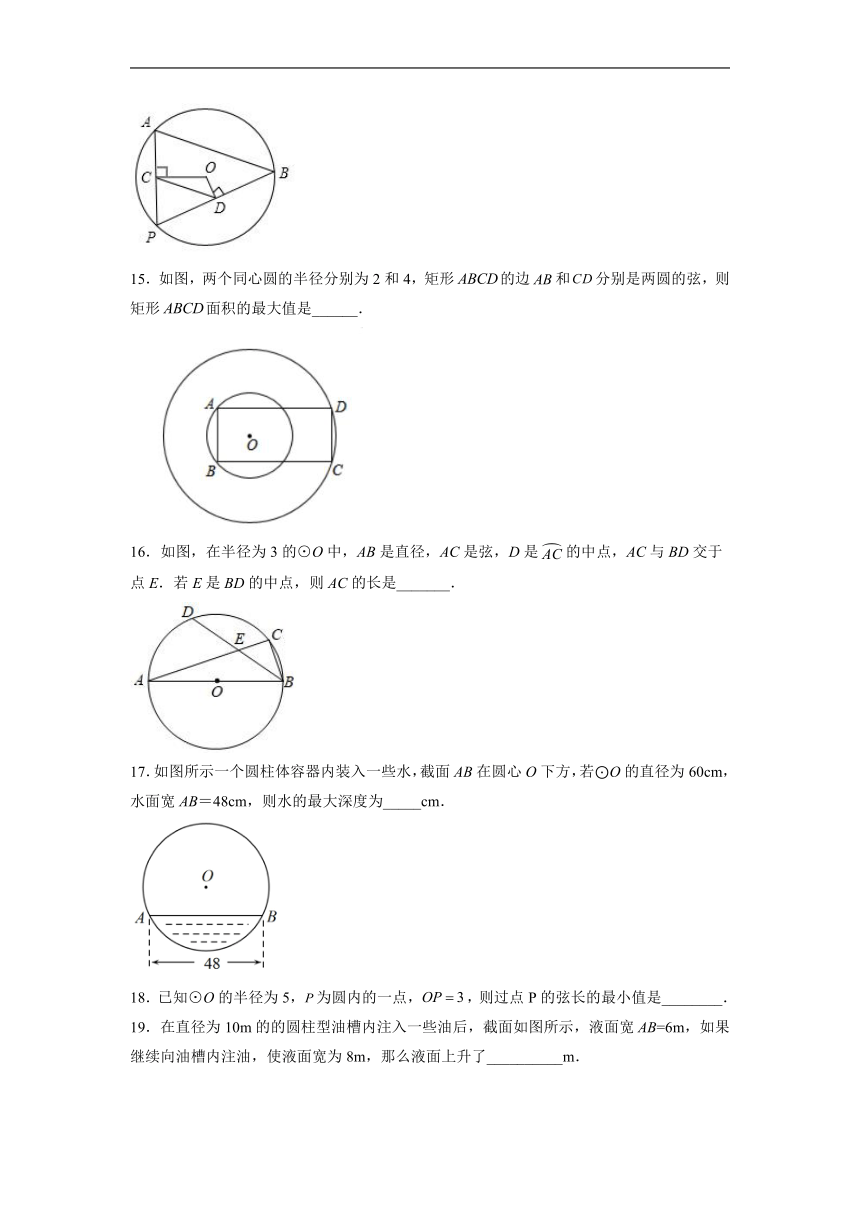
15.如图,两个同心圆的半径分别为2和4,矩形的边和分别是两圆的弦,则矩形面积的最大值是______.
16.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是_______.
17.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为60cm,水面宽AB=48cm,则水的最大深度为_____cm.
18.已知⊙O的半径为5,为圆内的一点,,则过点P的弦长的最小值是________.
19.在直径为10m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=6m,如果继续向油槽内注油,使液面宽为8m,那么液面上升了__________m.
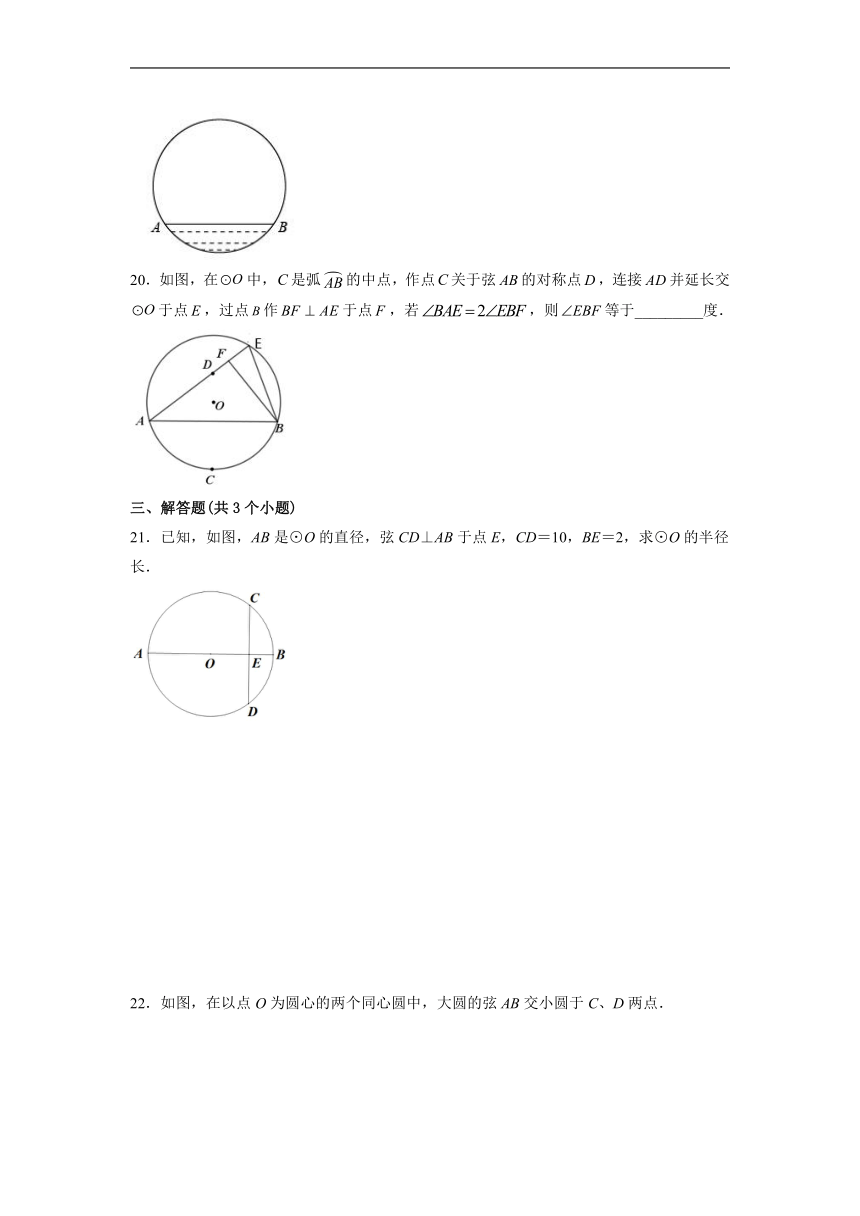
20.如图,在中,是弧的中点,作点关于弦的对称点,连接并延长交于点,过点作于点,若,则等于_________度.
三、解答题(共3个小题)
21.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=10,BE=2,求⊙O的半径长.
22.如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:AC=BD;
(2)连接OA、OC,若OA=6,OC=4,∠OCD=60°,求AC的长.
23.如图,在半径为2的扇形中,,点C是弧上的一个动点(不与点A、B重合),,垂足分别为D、E.
(1)当时,求线段的长;
(2)在中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)在中是否存在度数保持不变的角?如果存在,请指出并求其度数,如果不存在,请说明理由.
24.1.2 垂直于弦的直径解析
1.
【答案】A
【详解】解:如图,连接AO,
∵半径与点D,
∴,
∵,
∴根据勾股定理,,
∴,
∴.
故选A.
2.
【答案】A
【详解】解:根据题意和圆的性质知点C为的中点,
连接OC交AB于D,则OC⊥AB,AD=BD=AB=3,
在Rt△OAD中,OA=4,AD=3,
∴OD===,
∴CD=OC﹣OD=4﹣,
即点到弦所在直线的距离是(4﹣)米,
故选:A.
3.
【答案】A
【详解】解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:A.
4.
【答案】D
【详解】解: O为圆心的两个同心圆的圆心,大圆的弦AB与小圆相切于C点,
C点是AB的中点,即AC=BC==6;
并且OC⊥AB,在中,
由勾股定理得,
所以;AO=8cm,
所以,
所以OC=
故选:
5.
【答案】A
【详解】解:过O作OD⊥AB于D,连接OA,
∵OA=10,AB=16,
∴AD=AB=×16=8,
∴OD==6,
∴OD≤OM≤OA,即6≤OM≤10.
∴OM不可能为5,
故选:A.
6.
【答案】D
【详解】根据垂径定理及其推论进行判断.
【解答】解:根据垂径定理,
①正确;
②错误.平分弦(不是直径)的直径平分弦所对的弧;
③错误.垂直于弦且平分弦的直线必过圆心;
④正确.
故选:D.
7.
【答案】A
【详解】解:第一块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
8.
【答案】C
【详解】解:设圆材的圆心为O,延长CD,交⊙O于点E,连接OA,如图所示:
由题意知:CE过点O,且,
则.
设圆形木材半径为r,
则,.
∵,
∴,
解得 ,
即⊙O的半径为13寸,
∴⊙O的直径为26寸.
故选:C.
9.
【答案】C
【详解】解:∵OD⊥BC,
∴CD=BD,
∵OA=OB,AC=4
∴OD=AC=2.
故选C.
10.
【答案】D
【详解】解:①当弦AB和CD在圆心同侧时,如图1,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∴OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12-5=7cm;
∴四边形ACDB的面积
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴.AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴四边形ACDB的面积
∴四边形ACDB的面积为119或289.
故选D.
11.
【答案】
【详解】解:∵⊙O的直径CD垂直弦AB于点E,AB=6,
∴BE=3,∠OEB=90°,
设OB=x,则OC=x,
∵CE=2,
∴OE=x-2,
∵在Rt△OBE中,,
∴,解得:,
∴,即⊙O的半径为,
故答案为:.
12.
【答案】8
【详解】解:∵OC为半径,OC⊥AB,
∴AB=2AD,
∵,
∴,
∴AB=2AD=8.
故答案为:8
13.
【答案】
【详解】如图,连接OF,过点O作OH⊥EF,垂足为H,
则EH=FH=EF=2,
∵GB=5,
∴OF=OB=,
在△OHF中,勾股定理,得
OH=,
∵四边形ABCD是矩形,
∴四边形OADH也是矩形,
∴AD=OH=,
故答案为:.
14.
【答案】4
【详解】解:∵,,
∴,,
∴是的中位线,
∴.
故答案为:4.
15.
【答案】16
【详解】解:过点O作OP⊥AB于P并反向延长交CD于N,作OM⊥AD于点M,连接OA、OD
∴AO=2,OD=4,四边形APND和四边形PBCN为矩形,PN⊥CD,
∴OM=AP
根据垂径定理可得:点P和点N分别为AB和CD的中点,
∴S矩形APND=S矩形ABCD
∵△AOD的高OM等于矩形APND的宽,△AOD的底为矩形APND的长
∴S△AOD=S矩形APND=S矩形ABCD
∴S矩形ABCD最大时,S△AOD也最大
过点D作AO边上的高h,根据垂线段最短可得h≤OD(当且仅当OD⊥OA时,取等号)
∴S△AOD=AO·h≤AO·OD=×2×4=4
故S△AOD的最大值为4
∴S矩形ABCD的最大值为4÷=16
故答案为:16.
16.
【答案】
【详解】解:如图,连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中,
, ∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,AB=2OD=6,
∴BC=2,
∴.
故答案为:.
17.
【答案】12
【详解】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为60cm,
∴OB=OC=30cm,
在Rt△OBD中,OD===18(cm),
∴CD=OC﹣OD=30﹣18=12(cm),
即水的最大深度为12cm,
故答案为:12.
18.
【答案】8
【详解】过P点作弦AB,使AB⊥OP,则AB为过P点的最短的弦,
连结OA,
∵OP⊥AB,
∴AP=BP,
在Rt△AOP中,OA=5,OP=3,
∴AP=,
∴AB=2AP=8.
故答案为:8.
19.
【答案】1或7
【详解】解:连接OA,作OG⊥AB于G,
∵AB=6m,
∴AG=AB=3m,
∵油槽直径为10m,
∴OA=5m,
∴OG=4m,即弦AB的弦心距是4m,
同理当油面宽AB为8m时,弦心距是3m,
∴当油面没超过圆心O时,油上升了1m;
当油面超过圆心O时,油上升了7m.
故答案为:1或7.
20.
【答案】18
【详解】设∠EBF=x,则∠BAE=2x,连接OC交AB于点G,连接OB,BC,OD,如下图所示
∵C是的中点,点O为圆心
∴OCAB(垂径定理)
又∵点C与点D关于弦AB对称
∴CDAB,且C,D,O三点共线,GD=GC
∴∠AGD=∠BGC=90°,GA=GB
故△AGD△BGC(SAS)
∴∠ADG=∠BCG=90°-2x
又∵OB=OC
∴∠OBC=∠OCB=∠ADC=90°-2x
又∵同弧
∠E=∠COB=180°-2∠OBC=180°-2(90°-2x)(在△OCB中)
∵BFAE
在△BEF中,∠E=90°-∠EBF=90°-x
故综上:180°-2(90°-2x)=90°-x
解得x=18°
故本题答案为:18
21.
【答案】⊙O的半径长为
【详解】连接OC
∵直径AB⊥CD
∴CE=DE,∠OEC=90°
∵CD=10
∴CE=DE=5
设半径为x,则OC=x,OE=x-2
在Rt△OEC中,,
∴,
∴x=
∴⊙O的半径长为.
22.
【答案】(1)见解析;(2)
【详解】(1)证明:过O作OH⊥CD于H,如图1所示:
∵OH⊥CD,
∴CH=DH,AH=BH,
∴AH﹣CH=BH﹣DH,
∴AC=BD;
(2)解:过O作OH⊥CD于H,连接OD,如图2所示:
则CH=DH=CD,
∵OC=OD,∠OCD=60°,
∴△OCD是等边三角形,
∴CD=OC=4,
∴CH=2,
∴OH===2,
∴AH===2,
∴AC=AH﹣CH=2﹣2.
23.
【答案】(1);(2)存在,中,的长度保持不变为
(3)存在,中,的度数保持不变为
【详解】(1)∵
∴
在中.
(2)存在,
连接
∵
∴,
∴
∴中,的长度保持不变为.
(3)存在,
连接
∵,
∴
同理:
∵
∴
∴
∴中,的度数保持不变为
一、单选题(共10个小题)
1.如图,AB为⊙O的弦,半径OC⊥AB于点D ,且AB=6,OD=4,则DC的长为( )
A.1 B.2 C.2.5 D.5
2.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.(4﹣)米 B.2米 C.3米 D.(4+)米
3.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1或7 B.7 C.1 D.3或4
4.如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于C点,AB=12cm,AO=8cm,则OC长为( )cm
A.5 B.4 C. D.
5.如图,⊙O的半径为10,弦AB=16,M是弦AB上的动点,则OM不可能为( )
A.5 B.6 C.7 D.8
6.下列说法正确的是( )
①平分弧的直径垂直平分弧所对的弦
②平分弦的直径平分弦所对的弧
③垂直于弦的直线必过圆心
④垂直于弦的直径平分弦所对的弧
A.②③ B.①③ C.②④ D.①④
7.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
8.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为( )
A.22寸 B.24寸 C.26寸 D.28寸
9.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
A.1 B.1.5 C.2 D.2.5
10.已知⊙O的半径为13,弦AB∥CD,AB=24,CD=10,则四边形ACDB的面积是( )
A.119 B.289 C.77或119 D.119或289
二、填空题(共10个小题)
11.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=6,则⊙O半径为_______.
12.如图,已知⊙O 中,半径 OC 垂直于弦 AB,垂足为 D, 若 ,则 AB 的长是__________.
13.如图,矩形ABCD与圆心在AB上的☉O交于点G,B,F,E, GB =5,EF =4,那么AD =__________.
14.如图,是⊙O的弦,长为8,是⊙O上一个动点(不与、重合),过点作于点,于点,则的长为________.
15.如图,两个同心圆的半径分别为2和4,矩形的边和分别是两圆的弦,则矩形面积的最大值是______.
16.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是_______.
17.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为60cm,水面宽AB=48cm,则水的最大深度为_____cm.
18.已知⊙O的半径为5,为圆内的一点,,则过点P的弦长的最小值是________.
19.在直径为10m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=6m,如果继续向油槽内注油,使液面宽为8m,那么液面上升了__________m.
20.如图,在中,是弧的中点,作点关于弦的对称点,连接并延长交于点,过点作于点,若,则等于_________度.
三、解答题(共3个小题)
21.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=10,BE=2,求⊙O的半径长.
22.如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点.
(1)求证:AC=BD;
(2)连接OA、OC,若OA=6,OC=4,∠OCD=60°,求AC的长.
23.如图,在半径为2的扇形中,,点C是弧上的一个动点(不与点A、B重合),,垂足分别为D、E.
(1)当时,求线段的长;
(2)在中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)在中是否存在度数保持不变的角?如果存在,请指出并求其度数,如果不存在,请说明理由.
24.1.2 垂直于弦的直径解析
1.
【答案】A
【详解】解:如图,连接AO,
∵半径与点D,
∴,
∵,
∴根据勾股定理,,
∴,
∴.
故选A.
2.
【答案】A
【详解】解:根据题意和圆的性质知点C为的中点,
连接OC交AB于D,则OC⊥AB,AD=BD=AB=3,
在Rt△OAD中,OA=4,AD=3,
∴OD===,
∴CD=OC﹣OD=4﹣,
即点到弦所在直线的距离是(4﹣)米,
故选:A.
3.
【答案】A
【详解】解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:A.
4.
【答案】D
【详解】解: O为圆心的两个同心圆的圆心,大圆的弦AB与小圆相切于C点,
C点是AB的中点,即AC=BC==6;
并且OC⊥AB,在中,
由勾股定理得,
所以;AO=8cm,
所以,
所以OC=
故选:
5.
【答案】A
【详解】解:过O作OD⊥AB于D,连接OA,
∵OA=10,AB=16,
∴AD=AB=×16=8,
∴OD==6,
∴OD≤OM≤OA,即6≤OM≤10.
∴OM不可能为5,
故选:A.
6.
【答案】D
【详解】根据垂径定理及其推论进行判断.
【解答】解:根据垂径定理,
①正确;
②错误.平分弦(不是直径)的直径平分弦所对的弧;
③错误.垂直于弦且平分弦的直线必过圆心;
④正确.
故选:D.
7.
【答案】A
【详解】解:第一块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
8.
【答案】C
【详解】解:设圆材的圆心为O,延长CD,交⊙O于点E,连接OA,如图所示:
由题意知:CE过点O,且,
则.
设圆形木材半径为r,
则,.
∵,
∴,
解得 ,
即⊙O的半径为13寸,
∴⊙O的直径为26寸.
故选:C.
9.
【答案】C
【详解】解:∵OD⊥BC,
∴CD=BD,
∵OA=OB,AC=4
∴OD=AC=2.
故选C.
10.
【答案】D
【详解】解:①当弦AB和CD在圆心同侧时,如图1,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∴OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12-5=7cm;
∴四边形ACDB的面积
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴.AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴四边形ACDB的面积
∴四边形ACDB的面积为119或289.
故选D.
11.
【答案】
【详解】解:∵⊙O的直径CD垂直弦AB于点E,AB=6,
∴BE=3,∠OEB=90°,
设OB=x,则OC=x,
∵CE=2,
∴OE=x-2,
∵在Rt△OBE中,,
∴,解得:,
∴,即⊙O的半径为,
故答案为:.
12.
【答案】8
【详解】解:∵OC为半径,OC⊥AB,
∴AB=2AD,
∵,
∴,
∴AB=2AD=8.
故答案为:8
13.
【答案】
【详解】如图,连接OF,过点O作OH⊥EF,垂足为H,
则EH=FH=EF=2,
∵GB=5,
∴OF=OB=,
在△OHF中,勾股定理,得
OH=,
∵四边形ABCD是矩形,
∴四边形OADH也是矩形,
∴AD=OH=,
故答案为:.
14.
【答案】4
【详解】解:∵,,
∴,,
∴是的中位线,
∴.
故答案为:4.
15.
【答案】16
【详解】解:过点O作OP⊥AB于P并反向延长交CD于N,作OM⊥AD于点M,连接OA、OD
∴AO=2,OD=4,四边形APND和四边形PBCN为矩形,PN⊥CD,
∴OM=AP
根据垂径定理可得:点P和点N分别为AB和CD的中点,
∴S矩形APND=S矩形ABCD
∵△AOD的高OM等于矩形APND的宽,△AOD的底为矩形APND的长
∴S△AOD=S矩形APND=S矩形ABCD
∴S矩形ABCD最大时,S△AOD也最大
过点D作AO边上的高h,根据垂线段最短可得h≤OD(当且仅当OD⊥OA时,取等号)
∴S△AOD=AO·h≤AO·OD=×2×4=4
故S△AOD的最大值为4
∴S矩形ABCD的最大值为4÷=16
故答案为:16.
16.
【答案】
【详解】解:如图,连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中,
, ∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,AB=2OD=6,
∴BC=2,
∴.
故答案为:.
17.
【答案】12
【详解】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为60cm,
∴OB=OC=30cm,
在Rt△OBD中,OD===18(cm),
∴CD=OC﹣OD=30﹣18=12(cm),
即水的最大深度为12cm,
故答案为:12.
18.
【答案】8
【详解】过P点作弦AB,使AB⊥OP,则AB为过P点的最短的弦,
连结OA,
∵OP⊥AB,
∴AP=BP,
在Rt△AOP中,OA=5,OP=3,
∴AP=,
∴AB=2AP=8.
故答案为:8.
19.
【答案】1或7
【详解】解:连接OA,作OG⊥AB于G,
∵AB=6m,
∴AG=AB=3m,
∵油槽直径为10m,
∴OA=5m,
∴OG=4m,即弦AB的弦心距是4m,
同理当油面宽AB为8m时,弦心距是3m,
∴当油面没超过圆心O时,油上升了1m;
当油面超过圆心O时,油上升了7m.
故答案为:1或7.
20.
【答案】18
【详解】设∠EBF=x,则∠BAE=2x,连接OC交AB于点G,连接OB,BC,OD,如下图所示
∵C是的中点,点O为圆心
∴OCAB(垂径定理)
又∵点C与点D关于弦AB对称
∴CDAB,且C,D,O三点共线,GD=GC
∴∠AGD=∠BGC=90°,GA=GB
故△AGD△BGC(SAS)
∴∠ADG=∠BCG=90°-2x
又∵OB=OC
∴∠OBC=∠OCB=∠ADC=90°-2x
又∵同弧
∠E=∠COB=180°-2∠OBC=180°-2(90°-2x)(在△OCB中)
∵BFAE
在△BEF中,∠E=90°-∠EBF=90°-x
故综上:180°-2(90°-2x)=90°-x
解得x=18°
故本题答案为:18
21.
【答案】⊙O的半径长为
【详解】连接OC
∵直径AB⊥CD
∴CE=DE,∠OEC=90°
∵CD=10
∴CE=DE=5
设半径为x,则OC=x,OE=x-2
在Rt△OEC中,,
∴,
∴x=
∴⊙O的半径长为.
22.
【答案】(1)见解析;(2)
【详解】(1)证明:过O作OH⊥CD于H,如图1所示:
∵OH⊥CD,
∴CH=DH,AH=BH,
∴AH﹣CH=BH﹣DH,
∴AC=BD;
(2)解:过O作OH⊥CD于H,连接OD,如图2所示:
则CH=DH=CD,
∵OC=OD,∠OCD=60°,
∴△OCD是等边三角形,
∴CD=OC=4,
∴CH=2,
∴OH===2,
∴AH===2,
∴AC=AH﹣CH=2﹣2.
23.
【答案】(1);(2)存在,中,的长度保持不变为
(3)存在,中,的度数保持不变为
【详解】(1)∵
∴
在中.
(2)存在,
连接
∵
∴,
∴
∴中,的长度保持不变为.
(3)存在,
连接
∵,
∴
同理:
∵
∴
∴
∴中,的度数保持不变为
同课章节目录
