2022—2023学年人教版数学九年级上册24.1.4 圆周角 课时练习 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册24.1.4 圆周角 课时练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 00:00:00 | ||
图片预览

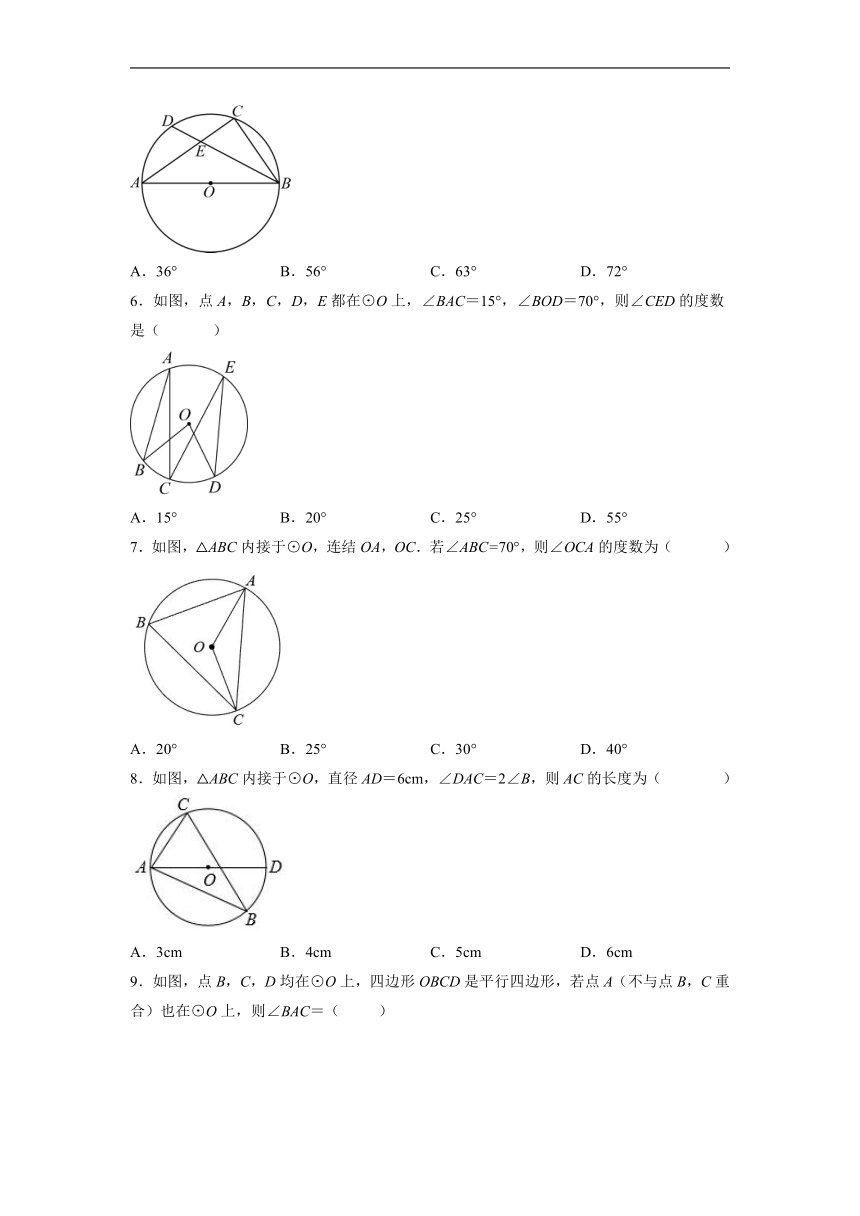
文档简介
24.1.4 圆周角(附解析)
一、单选题(共10个小题)
1.下列图形中的角是圆周角的是( )
A. B.C. D.
2.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12 B.10 C.4 D.5
3.如图,四边形ABCD内接于⊙O,AB为直径,∠C=120°.若AD=2,则AB的长为( )
A. B.2 C.2 D.4
4.如图,四边形是⊙O的内接四边形,且,,则的度数为( )
A. B. C. D.
5.如图,在半径为R的⊙O中,AB是直径,AC是弦,D为弧AC的中点,AC与BD交于点E,已知∠A=36°,则∠AED的度数为( )
A.36° B.56° C.63° D.72°
6.如图,点A,B,C,D,E都在⊙O上,∠BAC=15°,∠BOD=70°,则∠CED的度数是( )
A.15° B.20° C.25° D.55°
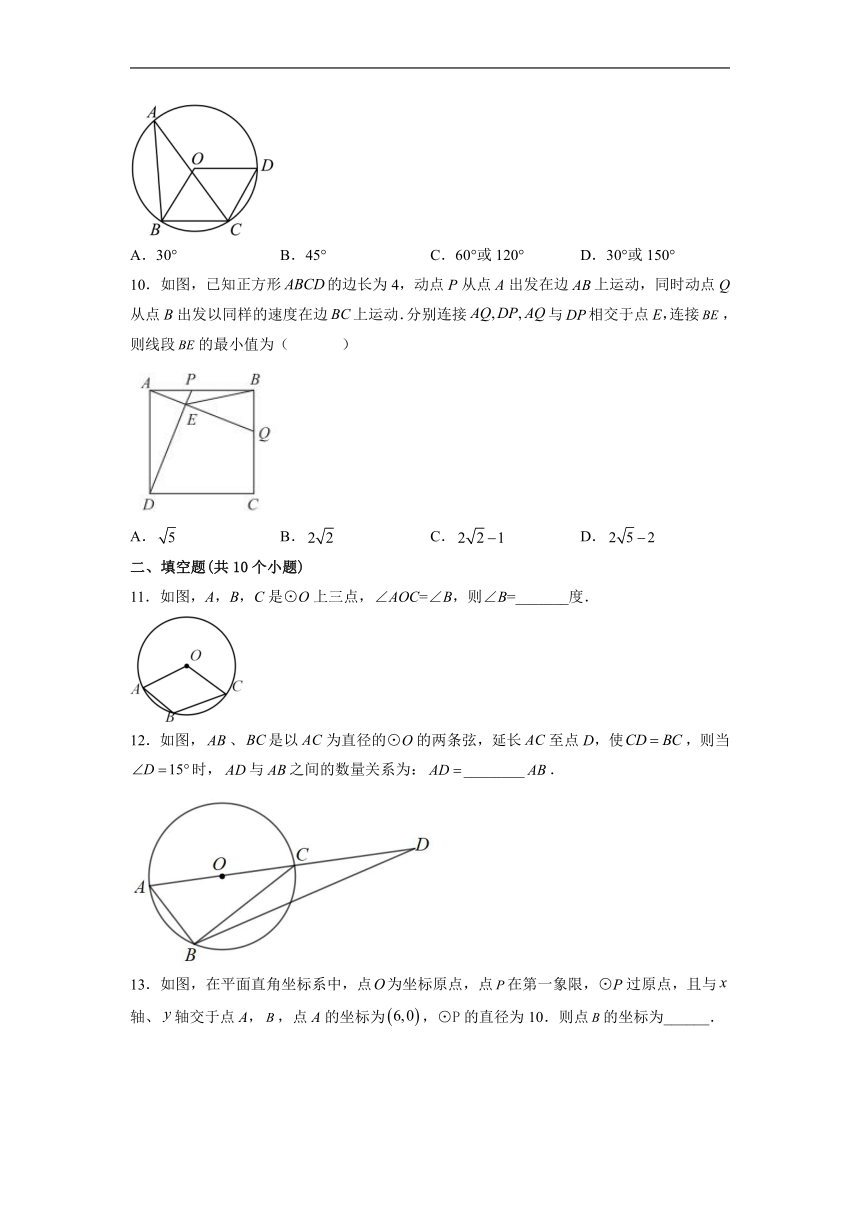
7.如图,△ABC内接于⊙O,连结OA,OC.若∠ABC=70°,则∠OCA的度数为( )
A.20° B.25° C.30° D.40°
8.如图,△ABC内接于⊙O,直径AD=6cm,∠DAC=2∠B,则AC的长度为( )
A.3cm B.4cm C.5cm D.6cm
9.如图,点B,C,D均在⊙O上,四边形OBCD是平行四边形,若点A(不与点B,C重合)也在⊙O上,则∠BAC=( )
A.30° B.45° C.60°或120° D.30°或150°
10.如图,已知正方形的边长为4,动点P从点A出发在边上运动,同时动点Q从点B出发以同样的速度在边上运动.分别连接与相交于点E,连接,则线段的最小值为( )
A. B. C. D.
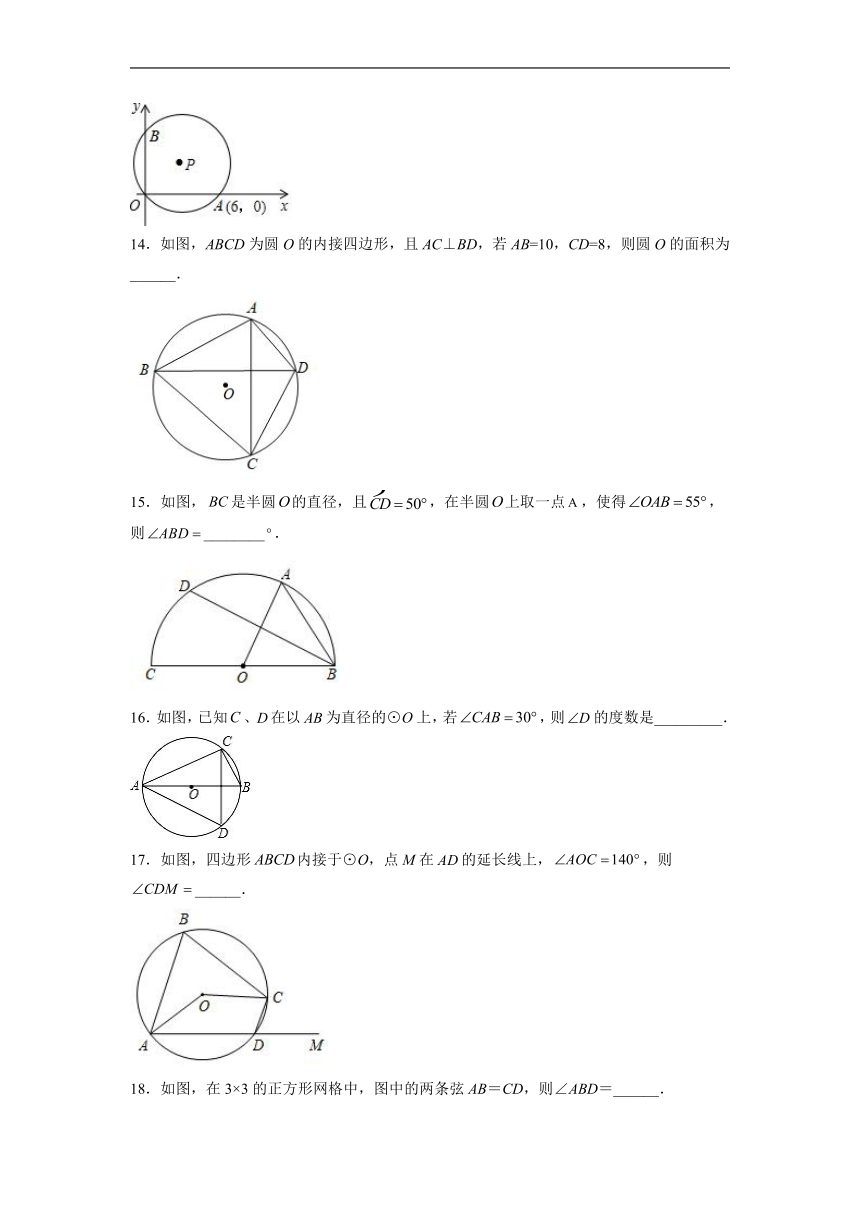
二、填空题(共10个小题)
11.如图,A,B,C是⊙O上三点,∠AOC=∠B,则∠B=_______度.
12.如图,、是以为直径的⊙O的两条弦,延长至点D,使,则当时,与之间的数量关系为:________.
13.如图,在平面直角坐标系中,点为坐标原点,点在第一象限,⊙P过原点,且与轴、轴交于点A,,点A的坐标为,⊙P的直径为10.则点的坐标为______.
14.如图,ABCD为圆O的内接四边形,且AC⊥BD,若AB=10,CD=8,则圆O的面积为______.
15.如图,是半圆的直径,且,在半圆上取一点,使得,则________.
16.如图,已知、在以为直径的⊙O上,若,则的度数是_________.
17.如图,四边形内接于⊙O,点M在的延长线上,,则______.
18.如图,在3×3的正方形网格中,图中的两条弦AB=CD,则∠ABD=______.
19.如图,是⊙O的弦,,点是上的一个动点,且,若点、分别是、的中点,则的最大值是______.
20.如图,AB,CD是⊙O的直径,弦BE与CD交于点F,F为BE中点,.若,则BC的长为______.
三、解答题(共3个小题)
21.在⊙O中,弦AB⊥AC,且AB=AC=6.D是⊙O上一点(不在上),连接AD、BD、CD.
(1)如图①,若AD经过圆心O,求BD、CD的长;
(2)如图②,若∠BAD=2∠DAC,连接BC、OD,且BC是直径,求BD、CD的长.
22.如图,AB为⊙O的直径,弦CD⊥AB于E,点F在DC的延长线上,AF交⊙O于G.
(1)求证:∠FGC=∠ACD;
(2)若AE=CD=8,试求⊙O的半径.
23.已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD=6,BD=8,求⊙O的半径和DE的长.
24.1.4 圆周角解析
1.
【答案】A
【详解】解:根据圆周角的定义可知,选项中的角是圆周角.
故选:.
2.
【答案】B
【详解】解:连接EF,
∵OE⊥OF,
∴∠EOF=90°
∴EF是直径
∴EF===10
故选:B.
3.
【答案】D
【详解】解:连接OD,
∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,
∵∠C=120°,
∴∠A=60°,
∵OD=OA,
∴△AOD是等边三角形,
∴AD=OD=OA,
∵AD=2,
∴OA=OD=OB=2,
∴AB=2+2=4,
故选:D.
4.
【答案】B
【详解】解:四边形是⊙O的内接四边形,
,
,
故选:B.
5.
【答案】C
【详解】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=36°,
∴∠ABC=90°﹣∠A=90°﹣36°=54°,
∵D为弧AC的中点,
∴,
∴,
∴∠AED=∠A+∠ABD=36°+27°=63°.
故选:C.
6.
【答案】B
【详解】:解:连接BE,
∵∠BOD=70°,
∴∠BED=∠BOD=35°,
∵∠BEC=∠BAC=15°,
∴∠CED=∠BED ∠BEC=35° 15°=20°,
故选:B.
7.
【答案】A
【详解】解:∵OA=OC,
∴∠OCA=∠OAC,
∵∠AOC=2∠ABC=2×70°=140°,
∴∠OCA==20°,
故选:A.
8.
【答案】A
【详解】解:连接CD,则∠D=∠B,
∵∠DAC=2∠B,
∴∠DAC=2∠D,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠DAC=90°,
∴3∠D=90°,
∴∠D=30°,
∴AC=AD=×6=3cm,
故选:A.
9.
【答案】D
【详解】解:(1)当点A在优弧BC上时,连接OC,
∵四边形OBCD是平行四边形,
∴BC=OD,
∴BC=OB=OC,
∴ΔOBC是等边三角形,
∴∠BOC=60°
∴∠BAC=∠BOC=30°;
(2)当点A在劣弧BC上位置时,连接OC,
∵四边形ABA'C为圆内接四边形,
∴∠BAC+∠BA'C=180°,
∵∠BAC=30°,
∴∠BA'C=150°.
综上∠BAC的度数为30°或150°.
故选:D.
10.
【答案】D
【详解】∵点P与点Q的速度相同,
∴AP=BQ,
∵四边形ABCD为正方形,
∴∠DAP=∠ABQ,AB=AD,
∴△DAP≌△ABQ(SAS),
∴∠ABP=∠DAQ,
∵∠ADP+∠BAQ=90°,
∵∠DAE+∠BAQ=90°,
∴∠DAE+∠ADE=90°,
∴点E在以AD为直径的圆上,圆心为点O,
如图,连接OB,与圆O的交点即为所求,
∵AD=4,
∴AB=4,AO=2,
∴,
∴BE的最小值为OB-2=,
故选:D.
11.
【答案】120
【详解】如图,连结OB,
∵OA=OB=OC,
∴△OAB和△OBC都是等腰三角形,
∴∠A=∠OBA,∠C=∠OBC,
∴∠ABC=∠OBA+∠OBC=∠A+∠C,
∴∠A+∠C=∠ABC=∠AOC
∵∠A+ ∠ABC+∠C+∠AOC=360゜
∴3∠ABC=360゜
∴∠ABC=120゜
即∠B=120゜.
故答案为:120.
12.
【答案】
【详解】解:设AB的边长为x,
∵,
∴,
∴,
∵AC是直径,
∴,
∴AC=2x,
根据勾股定理可得,
即,
∴,
∵,
∴,
故答案为:.
13.
【答案】
【详解】连接AB,
∵∠AOB=90°,
∴AB是直径,
∴AB=10.
又∵∠AOB=90°,点A的坐标为,
∴,,
∴,
∴点的坐标为.
故答案为:.
14.
【答案】
【详解】解:如图,连接,并延长交圆于点,连接,.
则,.
∵,
∴//,
∴
∴BE=CD,
∵
∴.
在Rt△中,AB=10,
所以,由勾股定理得,
∴.
所以圆的面积为.
15.
【答案】30
【详解】解:如下图,连接OD,
∵,
∴∠COD=50°,
∴∠CBD=∠COD=25°,
∵,OA=OB,
∴∠OBA=,
∴,
故答案为:30.
16.
【答案】
【详解】为⊙O的直径,
,
,
,
.
故答案为:60°.
17.
【答案】70°
【详解】解:∵,
∴,
∵四边形ABCD内接于⊙O,
∴,
∵,
∴,
故答案为:70°.
18.
【答案】
【详解】解:如图,
连接AD,BC,设CD与AB交于点E,
由网格特点知,.
∵AB=CD,
∴.
根据同弧所对的圆周角相等,可知.
∴,
∴,
∴,
故答案为:.
19.
【答案】
【详解】解:作直径,如图,
点、分别是、的中点,
为的中位线,
,
为直径,
,
,
,
当时,的值最大,
最大值为,的最大值为.
故答案为.
20.
【答案】
【详解】如图,连接AE.
∵F为BE中点,CD是的直径,
∴.
∵AB是⊙O的直径,
∴,
∴.
∵,
∴四边形AEDF为平行四边形,
∴.
∵F为BE中点,O为AB中点,
∴OF为中位线,
∴.
设,则,
∴,
∴,
∴,
∴.
∵,
∴,解得:(舍),
∴,,,
∴,
∴.
故答案为:.
21.
【答案】(1)BD=6,CD=6;(2),BD=
【详解】(1)解:AD是⊙O的直径,
∴∠C=∠B=90°,
∵AB⊥AC,
∴∠BAC=90°,
∴四边形ABDC是矩形,
∵AB=AC=6,
∴BD=AC=6,CD=AB=6;
(2)∵∠BAC=90°,∠BAD=2∠DAC,
∴∠BAD=60°,∠DAC=30°,
∴∠COD=2∠CAD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴CD=OC,
在Rt△ABC中,,
∴,
在Rt△BCD中,.
22.
【答案】(1)见解析;(2)5
【详解】(1)证明:∵AB为⊙O的直径,CD⊥AB,
∴AB垂直平分CD,
∴AC=AD,
∴∠ACD=∠D,
∵四边形AGCD内接于⊙O,
∴∠AGC+∠D=180°,
∵∠AGC+∠FGC=180°,
∴∠D=∠FGC,
∴∠ACD=∠FGC;
(2)连接OC,
∵AB为⊙O的直径,CD⊥AB,AE=CD=8,
∴CE=ED=4,
设OA=OC=r,则OE=8-r,
在Rt△COE中,,
即,解得r=5,即⊙O的半径为5.
23.
【答案】(1)见解析;(2)见解析;(3)半径是2.5;DE=2.4
【详解】(1)∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠1+∠3=∠5+∠3=90°,
∴∠1=∠5=∠2,
∴PD=PA,
∵∠4+∠2=∠1+∠3=90°,
∴∠3=∠4,
∴PD=PF,
∴PA=PF,即P是线段AF的中点;
(3)连接CD,
∵∠DAC=∠DBA =∠DCA,
∴CD=AD=3,
∵∠ADB=90°,BD=4
∴AB==5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4.即DE的长为2.4.
一、单选题(共10个小题)
1.下列图形中的角是圆周角的是( )
A. B.C. D.
2.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12 B.10 C.4 D.5
3.如图,四边形ABCD内接于⊙O,AB为直径,∠C=120°.若AD=2,则AB的长为( )
A. B.2 C.2 D.4
4.如图,四边形是⊙O的内接四边形,且,,则的度数为( )
A. B. C. D.
5.如图,在半径为R的⊙O中,AB是直径,AC是弦,D为弧AC的中点,AC与BD交于点E,已知∠A=36°,则∠AED的度数为( )
A.36° B.56° C.63° D.72°
6.如图,点A,B,C,D,E都在⊙O上,∠BAC=15°,∠BOD=70°,则∠CED的度数是( )
A.15° B.20° C.25° D.55°
7.如图,△ABC内接于⊙O,连结OA,OC.若∠ABC=70°,则∠OCA的度数为( )
A.20° B.25° C.30° D.40°
8.如图,△ABC内接于⊙O,直径AD=6cm,∠DAC=2∠B,则AC的长度为( )
A.3cm B.4cm C.5cm D.6cm
9.如图,点B,C,D均在⊙O上,四边形OBCD是平行四边形,若点A(不与点B,C重合)也在⊙O上,则∠BAC=( )
A.30° B.45° C.60°或120° D.30°或150°
10.如图,已知正方形的边长为4,动点P从点A出发在边上运动,同时动点Q从点B出发以同样的速度在边上运动.分别连接与相交于点E,连接,则线段的最小值为( )
A. B. C. D.
二、填空题(共10个小题)
11.如图,A,B,C是⊙O上三点,∠AOC=∠B,则∠B=_______度.
12.如图,、是以为直径的⊙O的两条弦,延长至点D,使,则当时,与之间的数量关系为:________.
13.如图,在平面直角坐标系中,点为坐标原点,点在第一象限,⊙P过原点,且与轴、轴交于点A,,点A的坐标为,⊙P的直径为10.则点的坐标为______.
14.如图,ABCD为圆O的内接四边形,且AC⊥BD,若AB=10,CD=8,则圆O的面积为______.
15.如图,是半圆的直径,且,在半圆上取一点,使得,则________.
16.如图,已知、在以为直径的⊙O上,若,则的度数是_________.
17.如图,四边形内接于⊙O,点M在的延长线上,,则______.
18.如图,在3×3的正方形网格中,图中的两条弦AB=CD,则∠ABD=______.
19.如图,是⊙O的弦,,点是上的一个动点,且,若点、分别是、的中点,则的最大值是______.
20.如图,AB,CD是⊙O的直径,弦BE与CD交于点F,F为BE中点,.若,则BC的长为______.
三、解答题(共3个小题)
21.在⊙O中,弦AB⊥AC,且AB=AC=6.D是⊙O上一点(不在上),连接AD、BD、CD.
(1)如图①,若AD经过圆心O,求BD、CD的长;
(2)如图②,若∠BAD=2∠DAC,连接BC、OD,且BC是直径,求BD、CD的长.
22.如图,AB为⊙O的直径,弦CD⊥AB于E,点F在DC的延长线上,AF交⊙O于G.
(1)求证:∠FGC=∠ACD;
(2)若AE=CD=8,试求⊙O的半径.
23.已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD=6,BD=8,求⊙O的半径和DE的长.
24.1.4 圆周角解析
1.
【答案】A
【详解】解:根据圆周角的定义可知,选项中的角是圆周角.
故选:.
2.
【答案】B
【详解】解:连接EF,
∵OE⊥OF,
∴∠EOF=90°
∴EF是直径
∴EF===10
故选:B.
3.
【答案】D
【详解】解:连接OD,
∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,
∵∠C=120°,
∴∠A=60°,
∵OD=OA,
∴△AOD是等边三角形,
∴AD=OD=OA,
∵AD=2,
∴OA=OD=OB=2,
∴AB=2+2=4,
故选:D.
4.
【答案】B
【详解】解:四边形是⊙O的内接四边形,
,
,
故选:B.
5.
【答案】C
【详解】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=36°,
∴∠ABC=90°﹣∠A=90°﹣36°=54°,
∵D为弧AC的中点,
∴,
∴,
∴∠AED=∠A+∠ABD=36°+27°=63°.
故选:C.
6.
【答案】B
【详解】:解:连接BE,
∵∠BOD=70°,
∴∠BED=∠BOD=35°,
∵∠BEC=∠BAC=15°,
∴∠CED=∠BED ∠BEC=35° 15°=20°,
故选:B.
7.
【答案】A
【详解】解:∵OA=OC,
∴∠OCA=∠OAC,
∵∠AOC=2∠ABC=2×70°=140°,
∴∠OCA==20°,
故选:A.
8.
【答案】A
【详解】解:连接CD,则∠D=∠B,
∵∠DAC=2∠B,
∴∠DAC=2∠D,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠DAC=90°,
∴3∠D=90°,
∴∠D=30°,
∴AC=AD=×6=3cm,
故选:A.
9.
【答案】D
【详解】解:(1)当点A在优弧BC上时,连接OC,
∵四边形OBCD是平行四边形,
∴BC=OD,
∴BC=OB=OC,
∴ΔOBC是等边三角形,
∴∠BOC=60°
∴∠BAC=∠BOC=30°;
(2)当点A在劣弧BC上位置时,连接OC,
∵四边形ABA'C为圆内接四边形,
∴∠BAC+∠BA'C=180°,
∵∠BAC=30°,
∴∠BA'C=150°.
综上∠BAC的度数为30°或150°.
故选:D.
10.
【答案】D
【详解】∵点P与点Q的速度相同,
∴AP=BQ,
∵四边形ABCD为正方形,
∴∠DAP=∠ABQ,AB=AD,
∴△DAP≌△ABQ(SAS),
∴∠ABP=∠DAQ,
∵∠ADP+∠BAQ=90°,
∵∠DAE+∠BAQ=90°,
∴∠DAE+∠ADE=90°,
∴点E在以AD为直径的圆上,圆心为点O,
如图,连接OB,与圆O的交点即为所求,
∵AD=4,
∴AB=4,AO=2,
∴,
∴BE的最小值为OB-2=,
故选:D.
11.
【答案】120
【详解】如图,连结OB,
∵OA=OB=OC,
∴△OAB和△OBC都是等腰三角形,
∴∠A=∠OBA,∠C=∠OBC,
∴∠ABC=∠OBA+∠OBC=∠A+∠C,
∴∠A+∠C=∠ABC=∠AOC
∵∠A+ ∠ABC+∠C+∠AOC=360゜
∴3∠ABC=360゜
∴∠ABC=120゜
即∠B=120゜.
故答案为:120.
12.
【答案】
【详解】解:设AB的边长为x,
∵,
∴,
∴,
∵AC是直径,
∴,
∴AC=2x,
根据勾股定理可得,
即,
∴,
∵,
∴,
故答案为:.
13.
【答案】
【详解】连接AB,
∵∠AOB=90°,
∴AB是直径,
∴AB=10.
又∵∠AOB=90°,点A的坐标为,
∴,,
∴,
∴点的坐标为.
故答案为:.
14.
【答案】
【详解】解:如图,连接,并延长交圆于点,连接,.
则,.
∵,
∴//,
∴
∴BE=CD,
∵
∴.
在Rt△中,AB=10,
所以,由勾股定理得,
∴.
所以圆的面积为.
15.
【答案】30
【详解】解:如下图,连接OD,
∵,
∴∠COD=50°,
∴∠CBD=∠COD=25°,
∵,OA=OB,
∴∠OBA=,
∴,
故答案为:30.
16.
【答案】
【详解】为⊙O的直径,
,
,
,
.
故答案为:60°.
17.
【答案】70°
【详解】解:∵,
∴,
∵四边形ABCD内接于⊙O,
∴,
∵,
∴,
故答案为:70°.
18.
【答案】
【详解】解:如图,
连接AD,BC,设CD与AB交于点E,
由网格特点知,.
∵AB=CD,
∴.
根据同弧所对的圆周角相等,可知.
∴,
∴,
∴,
故答案为:.
19.
【答案】
【详解】解:作直径,如图,
点、分别是、的中点,
为的中位线,
,
为直径,
,
,
,
当时,的值最大,
最大值为,的最大值为.
故答案为.
20.
【答案】
【详解】如图,连接AE.
∵F为BE中点,CD是的直径,
∴.
∵AB是⊙O的直径,
∴,
∴.
∵,
∴四边形AEDF为平行四边形,
∴.
∵F为BE中点,O为AB中点,
∴OF为中位线,
∴.
设,则,
∴,
∴,
∴,
∴.
∵,
∴,解得:(舍),
∴,,,
∴,
∴.
故答案为:.
21.
【答案】(1)BD=6,CD=6;(2),BD=
【详解】(1)解:AD是⊙O的直径,
∴∠C=∠B=90°,
∵AB⊥AC,
∴∠BAC=90°,
∴四边形ABDC是矩形,
∵AB=AC=6,
∴BD=AC=6,CD=AB=6;
(2)∵∠BAC=90°,∠BAD=2∠DAC,
∴∠BAD=60°,∠DAC=30°,
∴∠COD=2∠CAD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴CD=OC,
在Rt△ABC中,,
∴,
在Rt△BCD中,.
22.
【答案】(1)见解析;(2)5
【详解】(1)证明:∵AB为⊙O的直径,CD⊥AB,
∴AB垂直平分CD,
∴AC=AD,
∴∠ACD=∠D,
∵四边形AGCD内接于⊙O,
∴∠AGC+∠D=180°,
∵∠AGC+∠FGC=180°,
∴∠D=∠FGC,
∴∠ACD=∠FGC;
(2)连接OC,
∵AB为⊙O的直径,CD⊥AB,AE=CD=8,
∴CE=ED=4,
设OA=OC=r,则OE=8-r,
在Rt△COE中,,
即,解得r=5,即⊙O的半径为5.
23.
【答案】(1)见解析;(2)见解析;(3)半径是2.5;DE=2.4
【详解】(1)∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠1+∠3=∠5+∠3=90°,
∴∠1=∠5=∠2,
∴PD=PA,
∵∠4+∠2=∠1+∠3=90°,
∴∠3=∠4,
∴PD=PF,
∴PA=PF,即P是线段AF的中点;
(3)连接CD,
∵∠DAC=∠DBA =∠DCA,
∴CD=AD=3,
∵∠ADB=90°,BD=4
∴AB==5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4.即DE的长为2.4.
同课章节目录
