24.3 正多边形和圆 课时练习 2022-2023学年九年级人教版数学上册(含解析)
文档属性
| 名称 | 24.3 正多边形和圆 课时练习 2022-2023学年九年级人教版数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 21:33:08 | ||
图片预览


文档简介
24.3 正多边形和圆(附解析)
一、单选题(共10个小题)
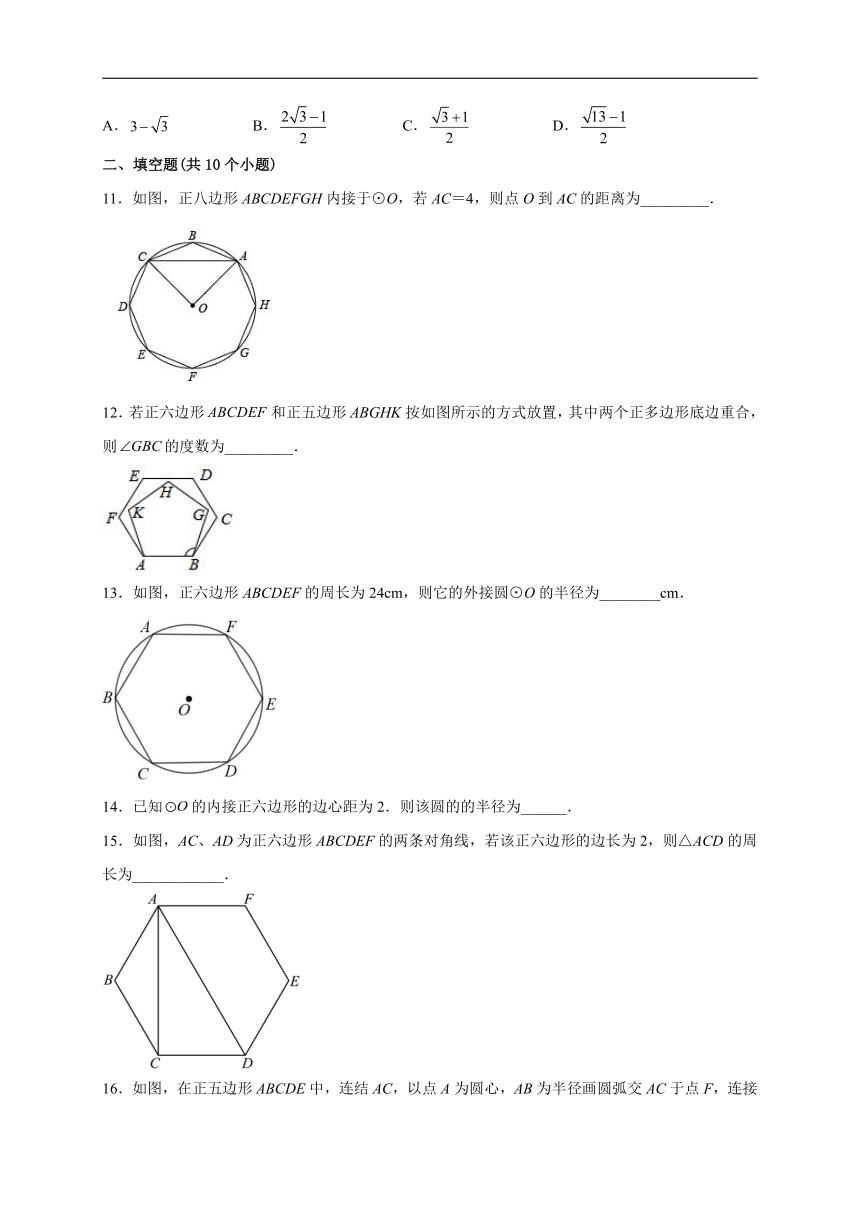
1.有一个正n边形的中心角是36°,则n为( )
A.7 B.8 C.9 D.10
2.如图,在圆内接正六边形ABCDEF中,BD,EC交于点G,已知半径为3,则EG的长为( )
A. B.3 C. D.6
3.如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( )
A.6 B.12 C.24 D.48
4.如图所示的图案,其外轮廓是一个正五边形,绕它的中心旋转一定的角度后能够与自身重合,则这个旋转角可能是( )
A. B. C. D.
5.若一个正多边形的中心角为40°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
6.⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )
A. B. C.2 D.2
7.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
8.如图,已知正六边形的边心距为3,则它的周长是( )
A.6 B.12 C. D.
9.如图,正五边形和正三角形都是的内接多边形,则的度数是( )
A. B. C. D.
10.已知四个正六边形如图摆放在图中,顶点A,B,C,D,E,F在圆上.若两个大正六边形的边长均为2,则小正六边形的边长是( )
A. B. C. D.
二、填空题(共10个小题)
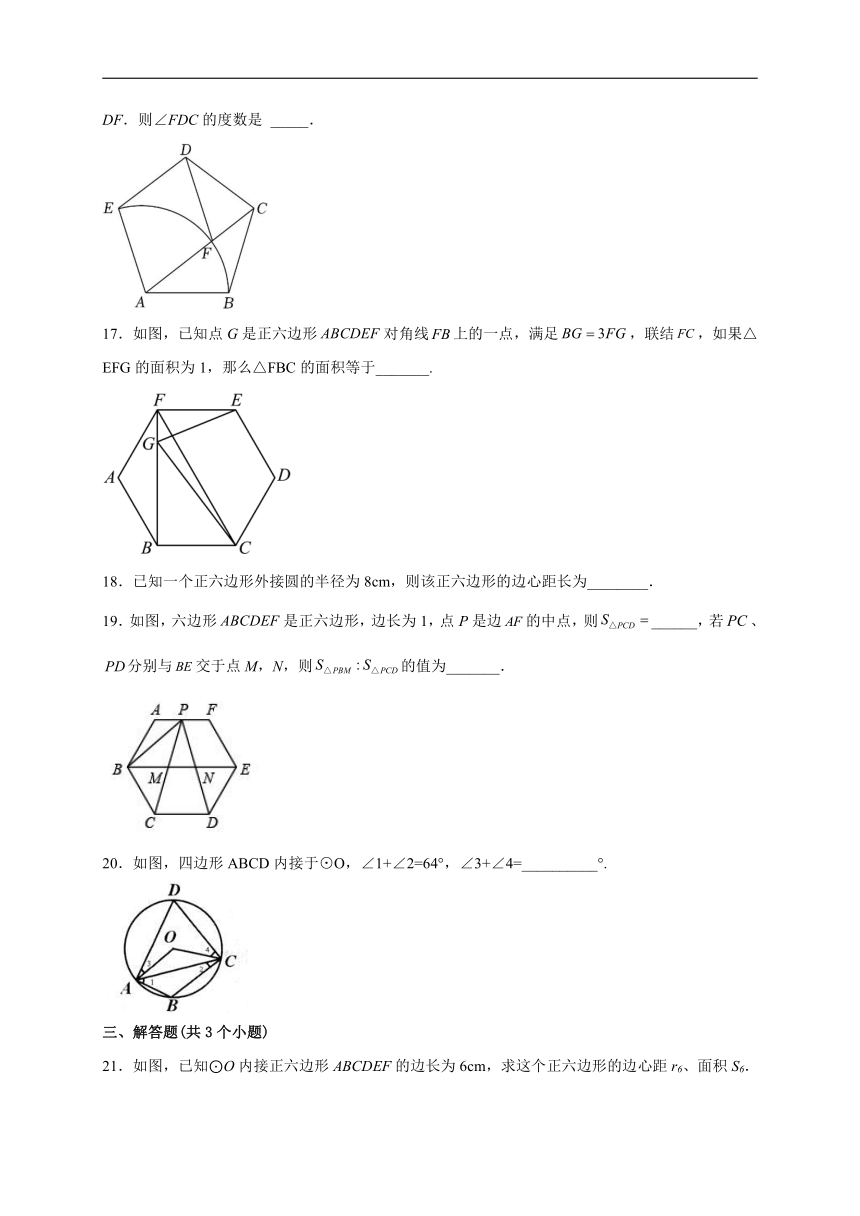
11.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC的距离为_________.
12.若正六边形和正五边形按如图所示的方式放置,其中两个正多边形底边重合,则的度数为_________.
13.如图,正六边形ABCDEF的周长为24cm,则它的外接圆⊙O的半径为________cm.
14.已知的内接正六边形的边心距为2.则该圆的的半径为______.
15.如图,AC、AD为正六边形ABCDEF的两条对角线,若该正六边形的边长为2,则△ACD的周长为____________.
16.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是 _____.
17.如图,已知点G是正六边形对角线上的一点,满足,联结,如果△EFG的面积为1,那么△FBC的面积等于_______.
18.已知一个正六边形外接圆的半径为8cm,则该正六边形的边心距长为________.
19.如图,六边形是正六边形,边长为1,点P是边的中点,则______,若、分别与交于点M,N,则的值为_______.
20.如图,四边形ABCD内接于⊙O,∠1+∠2=64°,∠3+∠4=__________°.
三、解答题(共3个小题)
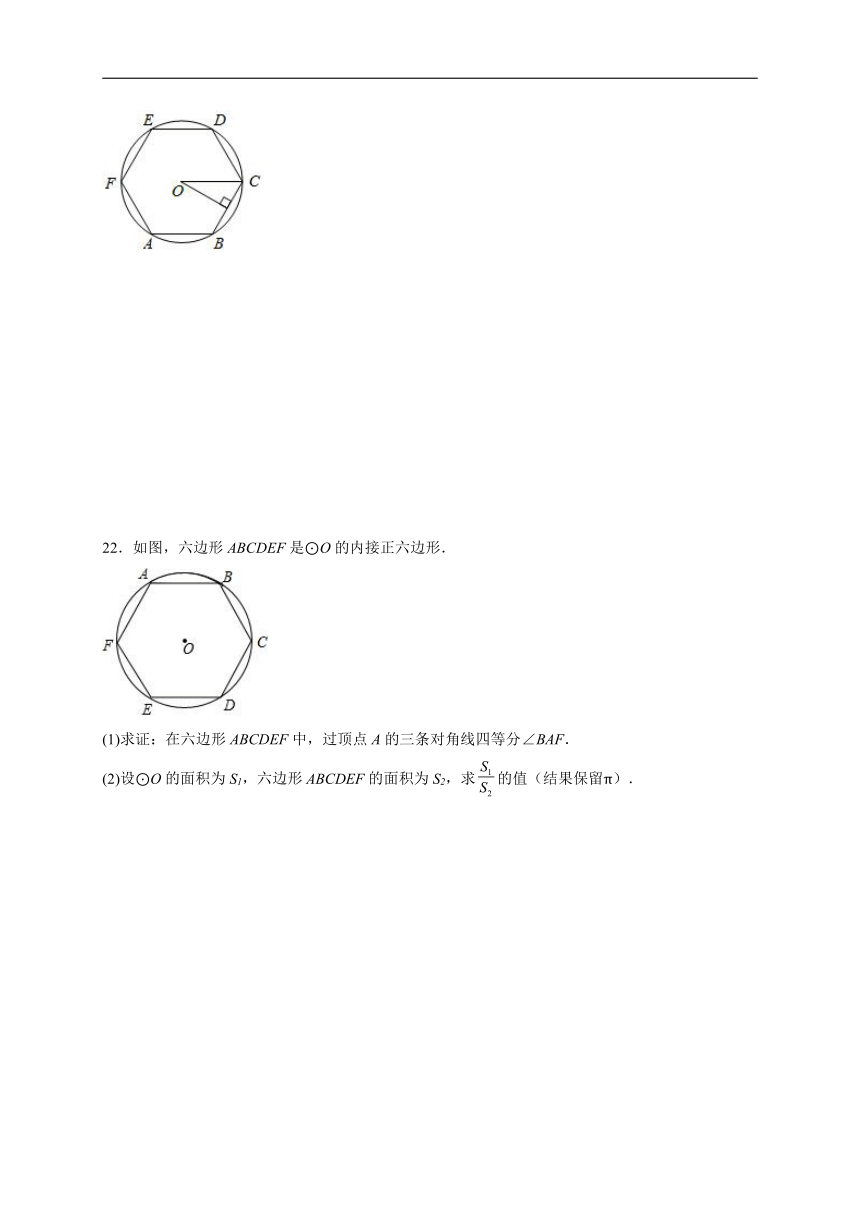
21.如图,已知⊙O内接正六边形ABCDEF的边长为6cm,求这个正六边形的边心距r6、面积S6.
22.如图,六边形ABCDEF是⊙O的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分∠BAF.
(2)设⊙O的面积为S1,六边形ABCDEF的面积为S2,求的值(结果保留π).
23.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
24.3 正多边形和圆解析
1.
【答案】D
【详解】解:,
故选:D.
2.
【答案】C
【详解】解:连接BE、GO,则BE经过O点,且O是BE的中点,
∵六边形ABCDEF是正六边形,
∴,
,
∵DE=EC,
∴,
∵,
∴,
∴,
设EG的长为x,则OG的长为,
∴,
解得:.
故选:C.
3.
【答案】C
【详解】解:连接OC,
∵AB是⊙O内接正六边形的一边,
∴∠AOB=360°÷6=60°,
∵BC是⊙O内接正八边形的一边,
∴∠BOC=360°÷8=45°,
∴∠AOC=∠AOB-∠BOC=60°-45°=15°
∴n=360°÷15°=24.
故选:C.
4.
【答案】B
【详解】解:正五边形的中心角,
绕它的中心旋转角度后能够与自身重合,
故选:B.
5.
【答案】A
【详解】解:设这个正多边形的边数是n,
由题意得:,
解得:n=9,
故选A.
6.
【答案】C
【详解】解:如图1,△ABC为⊙O的内接正三角形,作OM⊥BC于M,连接OB,
∵∠OBC=∠ABC=30°,
∴OM=OB=2;
如图2,四边形ABCD为⊙O的内接正方形,作ON⊥DC于N,连接OD,
∵∠ODC=∠ADC=45°,
∴ON=DN=OD=2;
如图3,六边形ABCDEF为⊙O的内接正六边形,作OH⊥DE于H,连接OE,
∵∠OED=∠FED=60°,
∴EH=OE=2,OH=EH=2,
∴半径为4的圆的内接正三角形、正方形、正六边形的边心距分别为2,2,2,
∵22+(2)2=(2)2,
∴以三条边心距所作的三角形为直角三角形,
∴该三角形的面积=×2×2=2.
故选:C.
7.
【答案】D
【详解】解:如图,连接,
四边形为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,
点在上,且是和的角平分线,,
,
,
,
恰好是圆O的一个内接正边形的一边,
,
故选:D.
8.
【答案】D
【详解】解:如图,过点作于点,
由题意得:边心距,
六边形是正六边形,
,
是等边三角形,
,
,
,
解得,
则正六边形的周长为,
故选:D.
9.
【答案】C
【详解】解:如图,连接.
是等边三角形,
,
,
是正五边形,
,
.
故选:C.
10.
【答案】D
【详解】解:如图,连接AD交PM于O,则点O是圆心,过点O作ON⊥DE于N,连接MF,取MF的中点G,连接GH,GQ,
由对称性可知,OM=OP=EN=DN=1,
由正六边形的性质可得ON=2,
∴ODOF,
∴MF1,
由正六边形的性质可知,△GFH、△GHQ、△GQM都是正三角形,
∴FHMF,
故选:D.
11.
【答案】2
【详解】解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
12.
【答案】12°
【详解】解:∵在正六边形ABCDEF和正五边形ABGHK中,∠,∠,
∴∠GBC=∠ABC-∠ABG=120°-108°=12°,
故答案为:12°.
13.
【答案】4
【分析】先根据正六边形的性质求得△AOB是等边三角形,然后根据等边三角形的性质即可解答.
【详解】解:连接OA,OB,
∵正六边形ABCDEF
∴∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=24÷6=4(cm),即R=4cm.
故答案为4.
14.
【答案】
【详解】如图所示,连接OA、OB,过O作OM⊥AB于M,则OM=2
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴,
∴,
∴该圆的半径为
故答案为:.
15.
【答案】
【详解】解:∵正六边形ABCDEF,
∴∠B=∠BCD120°,AB=BC,
∴∠ACB=∠BCA=30°,
∴∠ACD=120°﹣30°=90°,
由对称性可得,AD是正六边形的对称轴,
∴∠ADC=∠ADE∠CDE=60°,
在Rt△ACD中,CD=2,∠ADC=60°,
∴AD=2CD=4,ACCD=2,
∴△ACD的周长为AC+CD+AD=22+4=26,
故答案为:26.
16.
【答案】36
【详解】解:∵正五边形ABCDE,
∴∠ABC=∠EAB==108°,AB=BC=CD=DE=AE,
∴∠ACB=∠BAC==36°,
∴∠EAC=∠DCA=108°﹣36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴DE∥AC,
又∵DE=AE=AF,
∴四边形AEDF是平行四边形,
∴AE∥DF,
∴∠DFC=∠EAC=72°=∠DCA,
∴∠FDC=180°﹣72°﹣72°=36°,
故答案为:36°.
17.
【答案】4
【详解】解:如图,连接CE,
,
,
六边形是正六边形,
AB=AF=EF=BC,,
,
,
,
,
四边形BCEF是平行四边形,
,
的面积为1,,
的面积为,
故答案为4.
18.
【答案】cm
【详解】解:如图:连接OA、OB,过点O作OG⊥AB于点G
∵在Rt△AOG中,OA=8,∠AOG=30°,
∴AG=4
∴OG= .
故答案为:cm.
19.
【答案】 3:8
【详解】(1),
(2),
由题意是△PCD的中位线,
,
,
,
,
,
,
20.
【答案】64
【详解】解:如图
∵四边形ABCD接于⊙O,
∴,
又∵△AOC为等腰三角形,
,
∵∠1+∠2=64°,
∴∠3+∠4=180°-64°-2∠5=116°-2∠5,+
∵∠1+∠2+∠B=180°,∠B+∠D=180°,
∴∠B=∠1+∠2=64°
∴∠O=2∠D=128°
在等腰三角形AOC中,
∵2∠5=180°-∠0=180°-128°=52°
∴∠3+∠4=116°-2∠5=116°-52°=64°
故答案为64;
21.
【答案】
【详解】解:如下图所示,连接OB,设OG⊥CB于G,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠COB=60°,OC=OB,
∴△COB是等边三角形,
∴OC=OB=6cm,
即⊙O的半径R=6cm,
∵OC=OB=6,OG⊥CB,
∴,
在Rt△COG中,(cm),
∴(cm2).
22.
【答案】(1)证明见解析;(2)
【详解】(1)证明:如图,连接AE,AD,AC,
∵六边形ABCDEF是⊙O的内接正六边形,
∴EF=ED=CD=BC,
∴,
∴∠FAE=∠EAD=∠DAC=∠CAB,
∴过顶点A的三条对角线四等分∠BAF;
(2)解:如图,过O作OG⊥DE于G,连接OE,
设⊙O的半径为r,
∵∠DOE60°,OD=OE=r,
∴△ODE是等边三角形,
∴DE=OD=r,∠OED=60°,
∴∠EOG=30°,
∴EGr,
∴OGr,
∴正六边形ABCDEF的面积=6rrr2,
∵⊙O的面积=πr2,
∴.
23.
【答案】(1);(2),;(3).
【详解】(1)如图,连接OB、OC,则,
∵△ABC是⊙O内接正三角形,
中心角∠BOC=,
∵点O是⊙O内接正三角形ABC的内心,
∴,
∴,
在和△ONC中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是⊙O内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是⊙O内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
一、单选题(共10个小题)
1.有一个正n边形的中心角是36°,则n为( )
A.7 B.8 C.9 D.10
2.如图,在圆内接正六边形ABCDEF中,BD,EC交于点G,已知半径为3,则EG的长为( )
A. B.3 C. D.6
3.如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( )
A.6 B.12 C.24 D.48
4.如图所示的图案,其外轮廓是一个正五边形,绕它的中心旋转一定的角度后能够与自身重合,则这个旋转角可能是( )
A. B. C. D.
5.若一个正多边形的中心角为40°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
6.⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )
A. B. C.2 D.2
7.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.6 B.8 C.10 D.12
8.如图,已知正六边形的边心距为3,则它的周长是( )
A.6 B.12 C. D.
9.如图,正五边形和正三角形都是的内接多边形,则的度数是( )
A. B. C. D.
10.已知四个正六边形如图摆放在图中,顶点A,B,C,D,E,F在圆上.若两个大正六边形的边长均为2,则小正六边形的边长是( )
A. B. C. D.
二、填空题(共10个小题)
11.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC的距离为_________.
12.若正六边形和正五边形按如图所示的方式放置,其中两个正多边形底边重合,则的度数为_________.
13.如图,正六边形ABCDEF的周长为24cm,则它的外接圆⊙O的半径为________cm.
14.已知的内接正六边形的边心距为2.则该圆的的半径为______.
15.如图,AC、AD为正六边形ABCDEF的两条对角线,若该正六边形的边长为2,则△ACD的周长为____________.
16.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是 _____.
17.如图,已知点G是正六边形对角线上的一点,满足,联结,如果△EFG的面积为1,那么△FBC的面积等于_______.
18.已知一个正六边形外接圆的半径为8cm,则该正六边形的边心距长为________.
19.如图,六边形是正六边形,边长为1,点P是边的中点,则______,若、分别与交于点M,N,则的值为_______.
20.如图,四边形ABCD内接于⊙O,∠1+∠2=64°,∠3+∠4=__________°.
三、解答题(共3个小题)
21.如图,已知⊙O内接正六边形ABCDEF的边长为6cm,求这个正六边形的边心距r6、面积S6.
22.如图,六边形ABCDEF是⊙O的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分∠BAF.
(2)设⊙O的面积为S1,六边形ABCDEF的面积为S2,求的值(结果保留π).
23.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
24.3 正多边形和圆解析
1.
【答案】D
【详解】解:,
故选:D.
2.
【答案】C
【详解】解:连接BE、GO,则BE经过O点,且O是BE的中点,
∵六边形ABCDEF是正六边形,
∴,
,
∵DE=EC,
∴,
∵,
∴,
∴,
设EG的长为x,则OG的长为,
∴,
解得:.
故选:C.
3.
【答案】C
【详解】解:连接OC,
∵AB是⊙O内接正六边形的一边,
∴∠AOB=360°÷6=60°,
∵BC是⊙O内接正八边形的一边,
∴∠BOC=360°÷8=45°,
∴∠AOC=∠AOB-∠BOC=60°-45°=15°
∴n=360°÷15°=24.
故选:C.
4.
【答案】B
【详解】解:正五边形的中心角,
绕它的中心旋转角度后能够与自身重合,
故选:B.
5.
【答案】A
【详解】解:设这个正多边形的边数是n,
由题意得:,
解得:n=9,
故选A.
6.
【答案】C
【详解】解:如图1,△ABC为⊙O的内接正三角形,作OM⊥BC于M,连接OB,
∵∠OBC=∠ABC=30°,
∴OM=OB=2;
如图2,四边形ABCD为⊙O的内接正方形,作ON⊥DC于N,连接OD,
∵∠ODC=∠ADC=45°,
∴ON=DN=OD=2;
如图3,六边形ABCDEF为⊙O的内接正六边形,作OH⊥DE于H,连接OE,
∵∠OED=∠FED=60°,
∴EH=OE=2,OH=EH=2,
∴半径为4的圆的内接正三角形、正方形、正六边形的边心距分别为2,2,2,
∵22+(2)2=(2)2,
∴以三条边心距所作的三角形为直角三角形,
∴该三角形的面积=×2×2=2.
故选:C.
7.
【答案】D
【详解】解:如图,连接,
四边形为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,
点在上,且是和的角平分线,,
,
,
,
恰好是圆O的一个内接正边形的一边,
,
故选:D.
8.
【答案】D
【详解】解:如图,过点作于点,
由题意得:边心距,
六边形是正六边形,
,
是等边三角形,
,
,
,
解得,
则正六边形的周长为,
故选:D.
9.
【答案】C
【详解】解:如图,连接.
是等边三角形,
,
,
是正五边形,
,
.
故选:C.
10.
【答案】D
【详解】解:如图,连接AD交PM于O,则点O是圆心,过点O作ON⊥DE于N,连接MF,取MF的中点G,连接GH,GQ,
由对称性可知,OM=OP=EN=DN=1,
由正六边形的性质可得ON=2,
∴ODOF,
∴MF1,
由正六边形的性质可知,△GFH、△GHQ、△GQM都是正三角形,
∴FHMF,
故选:D.
11.
【答案】2
【详解】解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
12.
【答案】12°
【详解】解:∵在正六边形ABCDEF和正五边形ABGHK中,∠,∠,
∴∠GBC=∠ABC-∠ABG=120°-108°=12°,
故答案为:12°.
13.
【答案】4
【分析】先根据正六边形的性质求得△AOB是等边三角形,然后根据等边三角形的性质即可解答.
【详解】解:连接OA,OB,
∵正六边形ABCDEF
∴∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=24÷6=4(cm),即R=4cm.
故答案为4.
14.
【答案】
【详解】如图所示,连接OA、OB,过O作OM⊥AB于M,则OM=2
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴,
∴,
∴该圆的半径为
故答案为:.
15.
【答案】
【详解】解:∵正六边形ABCDEF,
∴∠B=∠BCD120°,AB=BC,
∴∠ACB=∠BCA=30°,
∴∠ACD=120°﹣30°=90°,
由对称性可得,AD是正六边形的对称轴,
∴∠ADC=∠ADE∠CDE=60°,
在Rt△ACD中,CD=2,∠ADC=60°,
∴AD=2CD=4,ACCD=2,
∴△ACD的周长为AC+CD+AD=22+4=26,
故答案为:26.
16.
【答案】36
【详解】解:∵正五边形ABCDE,
∴∠ABC=∠EAB==108°,AB=BC=CD=DE=AE,
∴∠ACB=∠BAC==36°,
∴∠EAC=∠DCA=108°﹣36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴DE∥AC,
又∵DE=AE=AF,
∴四边形AEDF是平行四边形,
∴AE∥DF,
∴∠DFC=∠EAC=72°=∠DCA,
∴∠FDC=180°﹣72°﹣72°=36°,
故答案为:36°.
17.
【答案】4
【详解】解:如图,连接CE,
,
,
六边形是正六边形,
AB=AF=EF=BC,,
,
,
,
,
四边形BCEF是平行四边形,
,
的面积为1,,
的面积为,
故答案为4.
18.
【答案】cm
【详解】解:如图:连接OA、OB,过点O作OG⊥AB于点G
∵在Rt△AOG中,OA=8,∠AOG=30°,
∴AG=4
∴OG= .
故答案为:cm.
19.
【答案】 3:8
【详解】(1),
(2),
由题意是△PCD的中位线,
,
,
,
,
,
,
20.
【答案】64
【详解】解:如图
∵四边形ABCD接于⊙O,
∴,
又∵△AOC为等腰三角形,
,
∵∠1+∠2=64°,
∴∠3+∠4=180°-64°-2∠5=116°-2∠5,+
∵∠1+∠2+∠B=180°,∠B+∠D=180°,
∴∠B=∠1+∠2=64°
∴∠O=2∠D=128°
在等腰三角形AOC中,
∵2∠5=180°-∠0=180°-128°=52°
∴∠3+∠4=116°-2∠5=116°-52°=64°
故答案为64;
21.
【答案】
【详解】解:如下图所示,连接OB,设OG⊥CB于G,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠COB=60°,OC=OB,
∴△COB是等边三角形,
∴OC=OB=6cm,
即⊙O的半径R=6cm,
∵OC=OB=6,OG⊥CB,
∴,
在Rt△COG中,(cm),
∴(cm2).
22.
【答案】(1)证明见解析;(2)
【详解】(1)证明:如图,连接AE,AD,AC,
∵六边形ABCDEF是⊙O的内接正六边形,
∴EF=ED=CD=BC,
∴,
∴∠FAE=∠EAD=∠DAC=∠CAB,
∴过顶点A的三条对角线四等分∠BAF;
(2)解:如图,过O作OG⊥DE于G,连接OE,
设⊙O的半径为r,
∵∠DOE60°,OD=OE=r,
∴△ODE是等边三角形,
∴DE=OD=r,∠OED=60°,
∴∠EOG=30°,
∴EGr,
∴OGr,
∴正六边形ABCDEF的面积=6rrr2,
∵⊙O的面积=πr2,
∴.
23.
【答案】(1);(2),;(3).
【详解】(1)如图,连接OB、OC,则,
∵△ABC是⊙O内接正三角形,
中心角∠BOC=,
∵点O是⊙O内接正三角形ABC的内心,
∴,
∴,
在和△ONC中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是⊙O内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是⊙O内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
同课章节目录
