2022-2023学年度 人教版数学九年级下册第二十七章 相似 达标测试卷 (含答案)
文档属性
| 名称 | 2022-2023学年度 人教版数学九年级下册第二十七章 相似 达标测试卷 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 180.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 00:00:00 | ||
图片预览




文档简介
第二十七章 相似
一、选择题(每小题3分,共30分)
1.下列图形中,属于相似图形的是( )
2.下列各组线段中,是成比例线段的是( )
A.1,2,3,4 B.3,6,9,18
C.1,2,2,6 D.1,,4,3
3.已知△ABC∽△DEF,若∠A=40°,∠E=80°,则∠F的度数为( )
A.30° B.60° C.70° D.80°
4.如图,l1∥l2∥l3,BC=1,=,则AB的长为( )
A.4 B.2 C. D.
(第4题) (第5题)
5.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是( )
A.2:1 B.3:1 C.4:1 D.5:1
6.如图,在△ABC中,点D,E分别在边AB,AC上,下列条件不能判定△ADE与△ACB相似的是( )
A.∠AED=∠B B.=
C.AD·BC=DE·AC D.DE∥BC
(第6题) (第7题)
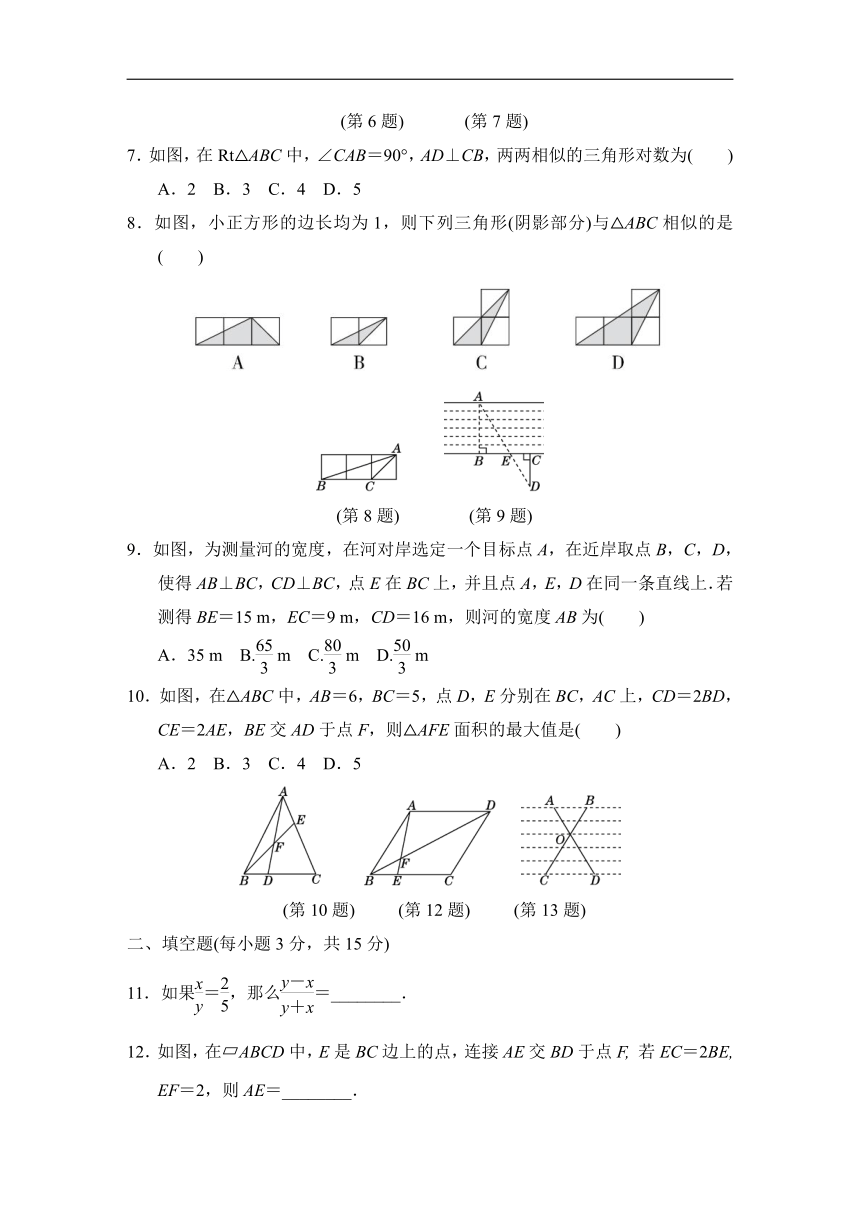
7.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB,两两相似的三角形对数为( )
A.2 B.3 C.4 D.5
8.如图,小正方形的边长均为1,则下列三角形(阴影部分)与△ABC相似的是( )
(第8题) (第9题)
9.如图,为测量河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=15 m,EC=9 m,CD=16 m,则河的宽度AB为( )
A.35 m B. m C. m D. m
10.如图,在△ABC中,AB=6,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是( )
A.2 B.3 C.4 D.5
(第10题) (第12题) (第13题)
二、填空题(每小题3分,共15分)
11.如果=,那么=________.
12.如图,在 ABCD中,E是BC边上的点,连接AE交BD于点F, 若EC=2BE, EF=2,则AE=________.
13.如图,有一组平行横格线,相邻横格线间的距离都相等,已知点A,B,C,D,O都在横格线上,且线段AD,BC交于点O,则ABCD等于________.
14.在平面直角坐标系中,点C,D的坐标分别为(2,3),(1,0),现以原点为位似中心,将线段CD放大得到线段AB,若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为__________.
15.如图,n个边长为1的相邻正方形的一边均在同一直线上,点P1,P2,P3,…,Pn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1P1的面积为S1,△B2C2P2的面积为S2,…,△BnCnPn的面积为Sn.
(1)S1=________;(2)Sn=________(用含n的式子表示).
三、解答题(一)(每小题8分,共24分)
16.若==,且3a+2b-4c=9,求a+b+c的值.
17.如图,△ABC在方格纸(小正方形的边长均为1)中.
(1)请在方格纸上建立平面直角坐标系,使点A的坐标为(3,4),点C的坐标为(7,3),并写出点B的坐标;
(2)以(1)中所建立的坐标系的原点O为位似中心,相似比为2?1,在第一象限内将△ABC放大,画出放大后的位似图形△A′B′C′;
(3)计算△A′B′C′的面积S.
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
(1)求证:△ABE∽△ECD;
(2)若AB=4,BE=,求CD的长.
四、解答题(二)(每小题9分,共27分)
19.如图,小强在地面E处放一个平面镜,刚好能从平面镜中看到教学楼的顶端B,此时EA=25米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼AB的高度.
20.如图,CD是Rt△ABC斜边AB上的高,E为CB的中点,ED的延长线交CA的延长线于点F.
求证:AC·CF=CB·DF.
21.如图,在梯形ABCD中, AD∥BC, AB⊥BC,∠AEB=∠ADC.
(1)求证:△ADE∽△DBC;
(2)连接EC,若CD2 =AD·BC ,求证:∠DCE=∠ADB.
五、解答题(三)(每小题12分,共24分)
22.如图,BC是⊙O的一条弦,过点O作OM⊥BC于点M,延长MO交⊙O于点A,连接AB,AC,∠ABC的平分线交AM于点D,交⊙O于点F,并与过点A的⊙O的切线交于点G.
(1)求证:AB=AG;
(2)连接AF,若AB=10,BC=12,求AF的长.
23.如图,在△ABC中,BA=BC=20 cm,AC=30 cm,点P从点A出发,沿AB以每秒4 cm的速度向点B运动;同时点Q从点C出发,沿CA以每秒3 cm的速度向点A运动,当其中一个动点停止,另一个动点也停止运动,设运动时间为x秒.
(1)当x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ与△CQB相似?若存在,求出此时AP的长;若不存在,请说明理由.
答案
一、1.D 2.B 3.B 4.C 5.C 6.C 7.B 8.B 9.C
10.A 点拨:连接DE,过点D作DH⊥AB于点H,如图.
∵CD=2BD,CE=2AE,∴==2,∴DE∥AB,
∴△CDE∽△CBA,△DEF∽△ABF,
∴=,=.易知=,∴==,
∴=,∴=,
∵DE∥AB,∴S△ABE=S△ABD,
∴S△ABE-S△ABF=S△ABD-S△ABF,
∴S△AEF=S△BDF=S△ABD.
∵AB=6,是定值,∴当DH最大时,△ABD的面积最大,
∵DH≤BD,易知BD=BC=,∴当DH=时,△ABD的面积最大,最大值为××6=5,
∴△AFE面积的最大值是×5=2.
二、11. 12.8 13.2∶3 14.(4,6)或(-4,-6)
15.(1) (2)
三、16.解:设===k(k≠0),则a=3k,b=5k,c=7k,代入3a+2b-4c=9,得9k+10k-28k=9,
解得k=-1,
∴a+b+c=15k=-15.
17.解:(1)建立平面直角坐标系如图所示.点B的坐标为(3,2).
(2)△A′B′C′如图所示.
(3)△A′B′C′的面积S为×4×8=16.
18.(1)证明:在Rt△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠AEC=∠B+∠BAE=∠AED+∠CED,
∠AED=45°,
∴∠BAE=∠CED,∴△ABE∽△ECD.
(2)解:在Rt△ABC中,∠BAC=90°,AB=AC=4,
∴BC=4 .∵BE=,∴EC=3 .
∵△ABE∽△ECD,∴=,即=,
解得CD=.
四、19.解:根据题意得∠AEB=∠CED,∠BAE=∠DCE=90°,∴△AEB∽△CDE,∴=,
即=,解得AB=16米.
答:教学楼AB的高度为16米.
20.证明:∵CD是Rt△ABC斜边AB上的高,E为CB的中点,
∴CE=EB=DE,∴∠B=∠BDE=∠FDA.
∵∠B+∠CAB=90°,∠FCD+∠CAB=90°,
∴∠B=∠FCD,∴∠FDA=∠FCD.
又∵∠F=∠F,∴△FDA∽△FCD,∴=.
∵∠ADC=∠CDB=90°,∠ACD=∠B,
∴△ACD∽△CBD,∴=,∴=,
即AC·CF=CB·DF.
21.证明:(1)∵AD∥BC,
∴∠ADE=∠DBC,∠ADC+∠C=180°,
∵∠AEB=∠ADC,∠AEB+∠AED=180°,
∴∠AED=∠C,∴△ADE∽△DBC.
(2)由(1)得△ADE∽△DBC,
∴=,∴DB·DE=AD·BC,
∵CD2=AD·BC,∴CD2=DB·DE,∴=.
又∵∠CDE=∠BDC,∴△CDE∽△BDC,
∴∠DCE=∠DBC,
∵∠ADB=∠DBC,∴∠DCE=∠ADB.
五、22. (1)证明:∵BG平分∠ABC,∴∠ABG=∠CBG,
∵AG是⊙O的切线,∴AG⊥AM,
∵AM⊥BC,∴AG∥BC,∴∠G=∠CBG,∴∠G=∠ABG,
∴AB=AG.
(2)解:设AC与BG交于点N,由(1)知AG=AB=10.
∵OM⊥BC,∴=,∴∠C=∠ABC,AC=AB=10,
∵AG∥BC,∴∠GAN=∠C,∴∠ABC=∠GAN,
∵∠GAN=∠GAF+∠FAN,∠ABC=∠FBC+∠ABG,∠FAN=∠FBC,
∴∠GAF=∠ABG.由(1)知∠G=∠ABG,
∴∠GAF=∠G,∴AF=GF.
∵AG∥BC,∴△GAN∽△BCN,
∴====,∴易得CN=,
设NG=5x,AF=GF=y(x>0,y>0),则BN=6x,
∴BG=11x,∵∠ABF=∠NBC,∠AFB=∠C,
∴△ABF∽△NBC,∴==,
∴==,解得x=,y=,∴AF=.
23.解:(1)由题意知,AP=4x cm,CQ=3x cm.
若PQ∥BC,则△APQ∽△ABC,∴=,
即=,解得x=,
∵∴0∴x=符合题意,即当x=时,PQ∥BC.
(2)存在.∵AB=BC,∴∠A=∠C,
分以下两种情况:
①当△APQ∽△CQB时,=,
即=,解得x1=,x2=0(舍去).
经检验,x=是上述方程的解.
∴当AP= cm时,△APQ∽△CQB;
②当△APQ∽△CBQ时,=,
即=,解得x3=5,x4=-10(舍去).
经检验,x=5是上述方程的解.
∴当AP=20 cm时,△APQ∽△CBQ.
综上所述,当AP的长为cm或20 cm时,△APQ与△CQB相似.
一、选择题(每小题3分,共30分)
1.下列图形中,属于相似图形的是( )
2.下列各组线段中,是成比例线段的是( )
A.1,2,3,4 B.3,6,9,18
C.1,2,2,6 D.1,,4,3
3.已知△ABC∽△DEF,若∠A=40°,∠E=80°,则∠F的度数为( )
A.30° B.60° C.70° D.80°
4.如图,l1∥l2∥l3,BC=1,=,则AB的长为( )
A.4 B.2 C. D.
(第4题) (第5题)
5.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是( )
A.2:1 B.3:1 C.4:1 D.5:1
6.如图,在△ABC中,点D,E分别在边AB,AC上,下列条件不能判定△ADE与△ACB相似的是( )
A.∠AED=∠B B.=
C.AD·BC=DE·AC D.DE∥BC
(第6题) (第7题)
7.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB,两两相似的三角形对数为( )
A.2 B.3 C.4 D.5
8.如图,小正方形的边长均为1,则下列三角形(阴影部分)与△ABC相似的是( )
(第8题) (第9题)
9.如图,为测量河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=15 m,EC=9 m,CD=16 m,则河的宽度AB为( )
A.35 m B. m C. m D. m
10.如图,在△ABC中,AB=6,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是( )
A.2 B.3 C.4 D.5
(第10题) (第12题) (第13题)
二、填空题(每小题3分,共15分)
11.如果=,那么=________.
12.如图,在 ABCD中,E是BC边上的点,连接AE交BD于点F, 若EC=2BE, EF=2,则AE=________.
13.如图,有一组平行横格线,相邻横格线间的距离都相等,已知点A,B,C,D,O都在横格线上,且线段AD,BC交于点O,则ABCD等于________.
14.在平面直角坐标系中,点C,D的坐标分别为(2,3),(1,0),现以原点为位似中心,将线段CD放大得到线段AB,若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为__________.
15.如图,n个边长为1的相邻正方形的一边均在同一直线上,点P1,P2,P3,…,Pn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1P1的面积为S1,△B2C2P2的面积为S2,…,△BnCnPn的面积为Sn.
(1)S1=________;(2)Sn=________(用含n的式子表示).
三、解答题(一)(每小题8分,共24分)
16.若==,且3a+2b-4c=9,求a+b+c的值.
17.如图,△ABC在方格纸(小正方形的边长均为1)中.
(1)请在方格纸上建立平面直角坐标系,使点A的坐标为(3,4),点C的坐标为(7,3),并写出点B的坐标;
(2)以(1)中所建立的坐标系的原点O为位似中心,相似比为2?1,在第一象限内将△ABC放大,画出放大后的位似图形△A′B′C′;
(3)计算△A′B′C′的面积S.
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
(1)求证:△ABE∽△ECD;
(2)若AB=4,BE=,求CD的长.
四、解答题(二)(每小题9分,共27分)
19.如图,小强在地面E处放一个平面镜,刚好能从平面镜中看到教学楼的顶端B,此时EA=25米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼AB的高度.
20.如图,CD是Rt△ABC斜边AB上的高,E为CB的中点,ED的延长线交CA的延长线于点F.
求证:AC·CF=CB·DF.
21.如图,在梯形ABCD中, AD∥BC, AB⊥BC,∠AEB=∠ADC.
(1)求证:△ADE∽△DBC;
(2)连接EC,若CD2 =AD·BC ,求证:∠DCE=∠ADB.
五、解答题(三)(每小题12分,共24分)
22.如图,BC是⊙O的一条弦,过点O作OM⊥BC于点M,延长MO交⊙O于点A,连接AB,AC,∠ABC的平分线交AM于点D,交⊙O于点F,并与过点A的⊙O的切线交于点G.
(1)求证:AB=AG;
(2)连接AF,若AB=10,BC=12,求AF的长.
23.如图,在△ABC中,BA=BC=20 cm,AC=30 cm,点P从点A出发,沿AB以每秒4 cm的速度向点B运动;同时点Q从点C出发,沿CA以每秒3 cm的速度向点A运动,当其中一个动点停止,另一个动点也停止运动,设运动时间为x秒.
(1)当x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ与△CQB相似?若存在,求出此时AP的长;若不存在,请说明理由.
答案
一、1.D 2.B 3.B 4.C 5.C 6.C 7.B 8.B 9.C
10.A 点拨:连接DE,过点D作DH⊥AB于点H,如图.
∵CD=2BD,CE=2AE,∴==2,∴DE∥AB,
∴△CDE∽△CBA,△DEF∽△ABF,
∴=,=.易知=,∴==,
∴=,∴=,
∵DE∥AB,∴S△ABE=S△ABD,
∴S△ABE-S△ABF=S△ABD-S△ABF,
∴S△AEF=S△BDF=S△ABD.
∵AB=6,是定值,∴当DH最大时,△ABD的面积最大,
∵DH≤BD,易知BD=BC=,∴当DH=时,△ABD的面积最大,最大值为××6=5,
∴△AFE面积的最大值是×5=2.
二、11. 12.8 13.2∶3 14.(4,6)或(-4,-6)
15.(1) (2)
三、16.解:设===k(k≠0),则a=3k,b=5k,c=7k,代入3a+2b-4c=9,得9k+10k-28k=9,
解得k=-1,
∴a+b+c=15k=-15.
17.解:(1)建立平面直角坐标系如图所示.点B的坐标为(3,2).
(2)△A′B′C′如图所示.
(3)△A′B′C′的面积S为×4×8=16.
18.(1)证明:在Rt△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠AEC=∠B+∠BAE=∠AED+∠CED,
∠AED=45°,
∴∠BAE=∠CED,∴△ABE∽△ECD.
(2)解:在Rt△ABC中,∠BAC=90°,AB=AC=4,
∴BC=4 .∵BE=,∴EC=3 .
∵△ABE∽△ECD,∴=,即=,
解得CD=.
四、19.解:根据题意得∠AEB=∠CED,∠BAE=∠DCE=90°,∴△AEB∽△CDE,∴=,
即=,解得AB=16米.
答:教学楼AB的高度为16米.
20.证明:∵CD是Rt△ABC斜边AB上的高,E为CB的中点,
∴CE=EB=DE,∴∠B=∠BDE=∠FDA.
∵∠B+∠CAB=90°,∠FCD+∠CAB=90°,
∴∠B=∠FCD,∴∠FDA=∠FCD.
又∵∠F=∠F,∴△FDA∽△FCD,∴=.
∵∠ADC=∠CDB=90°,∠ACD=∠B,
∴△ACD∽△CBD,∴=,∴=,
即AC·CF=CB·DF.
21.证明:(1)∵AD∥BC,
∴∠ADE=∠DBC,∠ADC+∠C=180°,
∵∠AEB=∠ADC,∠AEB+∠AED=180°,
∴∠AED=∠C,∴△ADE∽△DBC.
(2)由(1)得△ADE∽△DBC,
∴=,∴DB·DE=AD·BC,
∵CD2=AD·BC,∴CD2=DB·DE,∴=.
又∵∠CDE=∠BDC,∴△CDE∽△BDC,
∴∠DCE=∠DBC,
∵∠ADB=∠DBC,∴∠DCE=∠ADB.
五、22. (1)证明:∵BG平分∠ABC,∴∠ABG=∠CBG,
∵AG是⊙O的切线,∴AG⊥AM,
∵AM⊥BC,∴AG∥BC,∴∠G=∠CBG,∴∠G=∠ABG,
∴AB=AG.
(2)解:设AC与BG交于点N,由(1)知AG=AB=10.
∵OM⊥BC,∴=,∴∠C=∠ABC,AC=AB=10,
∵AG∥BC,∴∠GAN=∠C,∴∠ABC=∠GAN,
∵∠GAN=∠GAF+∠FAN,∠ABC=∠FBC+∠ABG,∠FAN=∠FBC,
∴∠GAF=∠ABG.由(1)知∠G=∠ABG,
∴∠GAF=∠G,∴AF=GF.
∵AG∥BC,∴△GAN∽△BCN,
∴====,∴易得CN=,
设NG=5x,AF=GF=y(x>0,y>0),则BN=6x,
∴BG=11x,∵∠ABF=∠NBC,∠AFB=∠C,
∴△ABF∽△NBC,∴==,
∴==,解得x=,y=,∴AF=.
23.解:(1)由题意知,AP=4x cm,CQ=3x cm.
若PQ∥BC,则△APQ∽△ABC,∴=,
即=,解得x=,
∵∴0
(2)存在.∵AB=BC,∴∠A=∠C,
分以下两种情况:
①当△APQ∽△CQB时,=,
即=,解得x1=,x2=0(舍去).
经检验,x=是上述方程的解.
∴当AP= cm时,△APQ∽△CQB;
②当△APQ∽△CBQ时,=,
即=,解得x3=5,x4=-10(舍去).
经检验,x=5是上述方程的解.
∴当AP=20 cm时,△APQ∽△CBQ.
综上所述,当AP的长为cm或20 cm时,△APQ与△CQB相似.
