数学人教A版(2019)选择性必修第一册2.3.3 点到直线的距离公式 课件(21张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.3 点到直线的距离公式 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 15:56:07 | ||
图片预览








文档简介
2.3.3 点到直线的距离公式
第二章 直线和圆的方程
探究新知
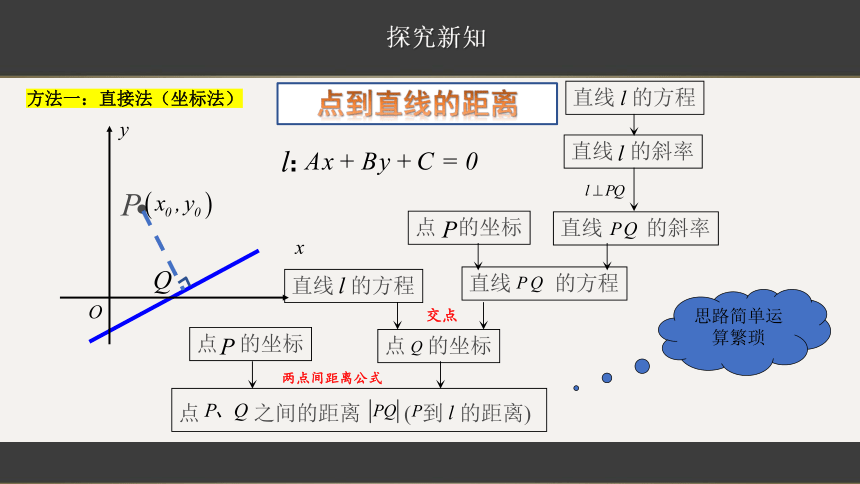
探究:如图,已知点?????????????????,??????????,直线 l :Ax + By + C=0,如何求点P到直线 l 的距离?
?
x
y
O
点 到直线 的距离,是指从点 到直线 的垂线段 的长度,其中 是垂足.
探究新知
点到直线的距离
P
.
直线 的方程
直线 的斜率
直线 的方程
交点
直线 的斜率
直线 的方程
点 的坐标
点 的坐标
点 的坐标
点 之间的距离 ( 到 的距离)
两点间距离公式
思路简单运算繁琐
方法一:直接法(坐标法)
设
P
.
①
②
③
④
探究新知
因此,点 到直线 的距离
探究新知
(1)方法:根据点到直线距离的定义,将点到直线距离转化为两点之间的距离.
(2)缺点:思路自然但运算量较大.
(3)思考:仔细观察求解过程, 思考引起复杂运算的原因是什么?
(4)对策:由此能否给出简化运算的方法?
解 密
反思:
探究新知
解 密
方法二:用设而不求法推导
????????=?????????02+?????????02?
?
②
对于②式,你能给出它的几何意义吗?
结合方程组①
能否直接求出(?????????????)????+(?????????????)????,进而求出????????呢?
?
请你试一试!
在上述方法中,若设垂足????的坐标为(????,?????),则
?
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
探究新知
解 密
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
①
????????=?????????02+?????????02?
?
②
由方程组
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
&?????????????????+??????????????????=?????????????+????????????+??????????????&???????????????????????????????????=?????????????????????????????????????????????????
?
?????????+?????????????????????????+????????+?????????????????????????=????????????+????????????+?????????
?
所以
?????????????????+?????????????????=????????????+????????????+?????????????????+????????
?
????????=?????????02+?????????02=????????0+????????0+????????2+????2
?
得
将(1)(2)两边平方后相加,得
可以验证,当A=0,或B=0时,公式仍然成立
所以
方法二:用设而不求法推导
探究新知
解 密
方法三:向量法
设????(????,?????)是直线 ?????上的任意一点,????是与直线 ?????的方向向量垂直的单位向量,则????????是????????在????上的投影向量
?
????????=?????????????
?
下面,利用直线 l 的方程得到与 l 的方向向量垂直的单位向量????.
?
如图,点P到直线 ???? 的距离,就是向量????????的模.
?
探究新知
解 密
方法三:向量法
设?????????????????,??????????,??????????????????,????????是直线l :Ax + By + C=0上的任意两点,
?
则????????????????=(??????????????????,?????????????????)是直线 l 的方向向量.
?
????????????+????????????+????=???? , ????????????+????????????+????=???? 两式相减,
?
因为,向量(A,B)与向量(??????????????????,?????????????????)垂直.
?
向量 ????????????+????????(????,????)是与直线???? 的方程向量垂直的一个单位向量.
?
取 ????=????????????+????????(????,????),从而
?
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????(?????????????+?????????????????=????????????+????????????????+??????????????????????????????????
?
得 ????(?????????????????)+????(?????????????????)=???? .
?
探究新知
解 密
因为M(x, y)在直线 l 上,所以 Ax + By + C=0,
所以 Ax + By =-C
得
?????????????=????????????+???????????????????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,
????????=????????=?????????????=????????????+????????????+????????????+?????????
?
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????????+??????????????????????????????????
?
方法三:向量法
探究新知
解 密
方法四:用三角形面积公式推导
y
O
x
S
R
Q
d
P
得
一、点到直线的距离
归纳总结:
因此,点 到直线 的距离
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①分子是P点代入直线方程;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}②分母是直线未知数x, y系数平方和的算术跟;
③运用此公式时要注意直线方程必须是一般式,若给出其他形式,应先化成一般式再用公式
一、点到直线的距离
例1 求点 到直线 的距离.
解:
思考:还有其他解法吗?
练一练
一、点到直线的距离
例2 已知△ABC的三个顶点分别是????(1,3),????(3,1),????(?1,0),求△ABC的面积.
?
y
1
2
3
4
x
O
-1
1
2
3
一、点到直线的距离
练1 求垂直于直线????+3????-5=0且与点????(-1,0)的距离是????????????????的直线????的方程.
?
练2 直线????通过直线7x+5y-24=0和?????????=0的交点,且点(5,1)到直线l的距离为???????? ,求直线????的方程.
?
一、点到直线的距离
例3 已知两条平行直线?????????:??????????????????????=???? ,????????:??????????????????????????=???? ,求 ????????与 ???????? 间的距离.
?
O
y
x
l2: 2x-7y-6=0
l1:2x-7y+8=0
两平行线间的
距离处处相等
?直线到直线的距离转化为点到直线的距离
如何取点,可使计算简单?
二、两条平行直线间的距离
两平行直线间的距离:
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
????
?
????
?
????
?
????2
?
????1
?
????
?
????
?
证明:两条平行线????????:????????+????????+????????=????与????????:????????+????????+????????=????之间的距离是
?
(2) 两直线方程中要求????,????的系数要相同.
?
(1) 把直线方程要化成一般式;
说明:
二、两条平行直线间的距离
练习
1.平行线????????+?????????????=????和????????+????????+????????=????的距离是______;
2.两平行线????????+????????=????????和????????+????????=????的距离是____.
?
例3 求与直线?????:5?????12????+6=0平行,且到??????的距离为2的直线的方程.
?
三、距离公式的综合用用
例4 已知????(????,????),则当点P到直线????????????+?????????=????的距离最大时,????=( )
?
1 B.????????? C. ???????? D. ????
?
例5 过点 ????(-????,????)引一直线,使它与点 ????(????,????),????(????,????)的距离相等,求该直线的方程.
?
三、距离公式的综合用用
例 6 已知点 ????(2,-1),求:
(1)过 P 点与原点距离为 2 的直线 ???? 的方程;
(2)过 P 点与原点距离最长的直线 ?????的方程并求出最大距离;
(3)是否存在过 P 点且与原点距离为 6 的直线?若存在,求出方程;若不存在,请说明理由.
?
三、距离公式的综合用用
例7 直线????:?????=????(????+????)?上存在两个不同点到原点距离等于????,则????的取值范围是( )
?
A . (-2,2) B. (?????,????) C.(-1,1) D. (??????????,??????????)
第二章 直线和圆的方程
探究新知
探究:如图,已知点?????????????????,??????????,直线 l :Ax + By + C=0,如何求点P到直线 l 的距离?
?
x
y
O
点 到直线 的距离,是指从点 到直线 的垂线段 的长度,其中 是垂足.
探究新知
点到直线的距离
P
.
直线 的方程
直线 的斜率
直线 的方程
交点
直线 的斜率
直线 的方程
点 的坐标
点 的坐标
点 的坐标
点 之间的距离 ( 到 的距离)
两点间距离公式
思路简单运算繁琐
方法一:直接法(坐标法)
设
P
.
①
②
③
④
探究新知
因此,点 到直线 的距离
探究新知
(1)方法:根据点到直线距离的定义,将点到直线距离转化为两点之间的距离.
(2)缺点:思路自然但运算量较大.
(3)思考:仔细观察求解过程, 思考引起复杂运算的原因是什么?
(4)对策:由此能否给出简化运算的方法?
解 密
反思:
探究新知
解 密
方法二:用设而不求法推导
????????=?????????02+?????????02?
?
②
对于②式,你能给出它的几何意义吗?
结合方程组①
能否直接求出(?????????????)????+(?????????????)????,进而求出????????呢?
?
请你试一试!
在上述方法中,若设垂足????的坐标为(????,?????),则
?
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
探究新知
解 密
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
①
????????=?????????02+?????????02?
?
②
由方程组
&?????????+??????????+?????==????&?????????????????=?????????????????????????
?
&?????????????????+??????????????????=?????????????+????????????+??????????????&???????????????????????????????????=?????????????????????????????????????????????????
?
?????????+?????????????????????????+????????+?????????????????????????=????????????+????????????+?????????
?
所以
?????????????????+?????????????????=????????????+????????????+?????????????????+????????
?
????????=?????????02+?????????02=????????0+????????0+????????2+????2
?
得
将(1)(2)两边平方后相加,得
可以验证,当A=0,或B=0时,公式仍然成立
所以
方法二:用设而不求法推导
探究新知
解 密
方法三:向量法
设????(????,?????)是直线 ?????上的任意一点,????是与直线 ?????的方向向量垂直的单位向量,则????????是????????在????上的投影向量
?
????????=?????????????
?
下面,利用直线 l 的方程得到与 l 的方向向量垂直的单位向量????.
?
如图,点P到直线 ???? 的距离,就是向量????????的模.
?
探究新知
解 密
方法三:向量法
设?????????????????,??????????,??????????????????,????????是直线l :Ax + By + C=0上的任意两点,
?
则????????????????=(??????????????????,?????????????????)是直线 l 的方向向量.
?
????????????+????????????+????=???? , ????????????+????????????+????=???? 两式相减,
?
因为,向量(A,B)与向量(??????????????????,?????????????????)垂直.
?
向量 ????????????+????????(????,????)是与直线???? 的方程向量垂直的一个单位向量.
?
取 ????=????????????+????????(????,????),从而
?
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????(?????????????+?????????????????=????????????+????????????????+??????????????????????????????????
?
得 ????(?????????????????)+????(?????????????????)=???? .
?
探究新知
解 密
因为M(x, y)在直线 l 上,所以 Ax + By + C=0,
所以 Ax + By =-C
得
?????????????=????????????+???????????????????????????????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}因此,
????????=????????=?????????????=????????????+????????????+????????????+?????????
?
?????????????=(??????????????,??????????????????????????+????????(????,????)=????????????+????????????????+??????????????????????????????????
?
方法三:向量法
探究新知
解 密
方法四:用三角形面积公式推导
y
O
x
S
R
Q
d
P
得
一、点到直线的距离
归纳总结:
因此,点 到直线 的距离
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①分子是P点代入直线方程;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}②分母是直线未知数x, y系数平方和的算术跟;
③运用此公式时要注意直线方程必须是一般式,若给出其他形式,应先化成一般式再用公式
一、点到直线的距离
例1 求点 到直线 的距离.
解:
思考:还有其他解法吗?
练一练
一、点到直线的距离
例2 已知△ABC的三个顶点分别是????(1,3),????(3,1),????(?1,0),求△ABC的面积.
?
y
1
2
3
4
x
O
-1
1
2
3
一、点到直线的距离
练1 求垂直于直线????+3????-5=0且与点????(-1,0)的距离是????????????????的直线????的方程.
?
练2 直线????通过直线7x+5y-24=0和?????????=0的交点,且点(5,1)到直线l的距离为???????? ,求直线????的方程.
?
一、点到直线的距离
例3 已知两条平行直线?????????:??????????????????????=???? ,????????:??????????????????????????=???? ,求 ????????与 ???????? 间的距离.
?
O
y
x
l2: 2x-7y-6=0
l1:2x-7y+8=0
两平行线间的
距离处处相等
?直线到直线的距离转化为点到直线的距离
如何取点,可使计算简单?
二、两条平行直线间的距离
两平行直线间的距离:
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
????
?
????
?
????
?
????2
?
????1
?
????
?
????
?
证明:两条平行线????????:????????+????????+????????=????与????????:????????+????????+????????=????之间的距离是
?
(2) 两直线方程中要求????,????的系数要相同.
?
(1) 把直线方程要化成一般式;
说明:
二、两条平行直线间的距离
练习
1.平行线????????+?????????????=????和????????+????????+????????=????的距离是______;
2.两平行线????????+????????=????????和????????+????????=????的距离是____.
?
例3 求与直线?????:5?????12????+6=0平行,且到??????的距离为2的直线的方程.
?
三、距离公式的综合用用
例4 已知????(????,????),则当点P到直线????????????+?????????=????的距离最大时,????=( )
?
1 B.????????? C. ???????? D. ????
?
例5 过点 ????(-????,????)引一直线,使它与点 ????(????,????),????(????,????)的距离相等,求该直线的方程.
?
三、距离公式的综合用用
例 6 已知点 ????(2,-1),求:
(1)过 P 点与原点距离为 2 的直线 ???? 的方程;
(2)过 P 点与原点距离最长的直线 ?????的方程并求出最大距离;
(3)是否存在过 P 点且与原点距离为 6 的直线?若存在,求出方程;若不存在,请说明理由.
?
三、距离公式的综合用用
例7 直线????:?????=????(????+????)?上存在两个不同点到原点距离等于????,则????的取值范围是( )
?
A . (-2,2) B. (?????,????) C.(-1,1) D. (??????????,??????????)
