2022年“国庆假期7件套”八年级上册:12.2 三角形全等的判定同步练习卷(7)(含解析)
文档属性
| 名称 | 2022年“国庆假期7件套”八年级上册:12.2 三角形全等的判定同步练习卷(7)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 452.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 20:50:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.2 三角形全等的判定 同步练习卷
一.选择题
1.如图,已知△ABC的三条边和三个角,则甲、乙、丙三个三角形中和△ABC全等的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.只有甲
2.如图,一块玻璃被打碎成三块,如果要去玻璃店配一块完全一样的玻璃,那么最合理的办法是( )
A.带①去 B.带②去 C.带③去 D.带①②③去
3.根据下列条件,能作出唯一的△ABC的是( )
A.AB=3,AC=4,∠B=30° B.AB=3,BC=4,AC=8
C.∠A=50°,∠B=60°,AB=4 D.∠C=90°,AB=5
4.如图,AB=DE,∠B=∠DEF,添加下列哪个条件,不能证明△ABC≌△DEF的是( )
A.∠A=∠D B.BC=EF C.AC=DF D.AC∥DF
5.如图,要测量河两岸相对的两点A,B之间的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长,则上述操作,判定△EDC≌△ABC的理由是( )
A.SSS B.ASA C.AAS D.SAS
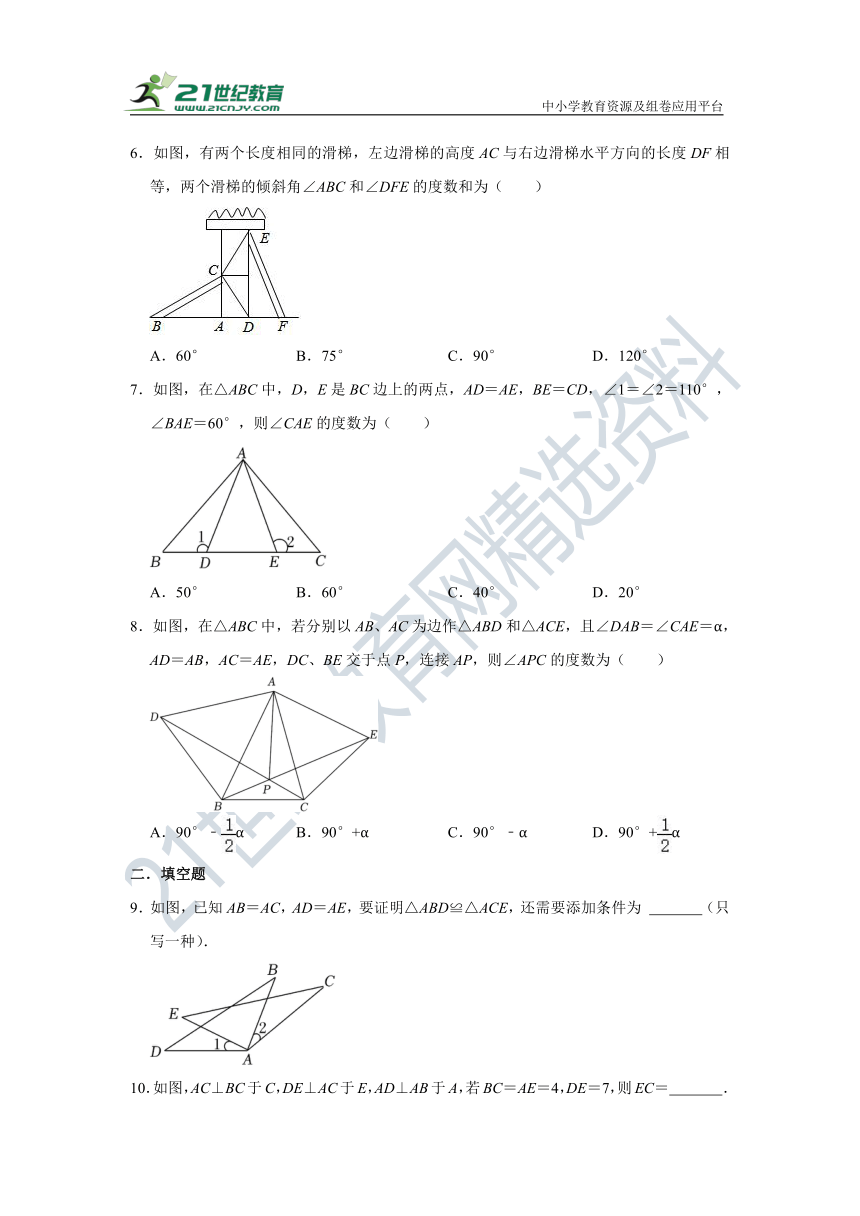
6.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A.60° B.75° C.90° D.120°
7.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
8.如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( )
A.90°﹣α B.90°+α C.90°﹣α D.90°+α
二.填空题
9.如图,已知AB=AC,AD=AE,要证明△ABD≌△ACE,还需要添加条件为 (只写一种).
10.如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,若BC=AE=4,DE=7,则EC= .
11.已知,如图,AD=CB,AB=CD,那么图中共有 对全等三角形.
12.如图,△ABC中,AB=AC,BF=CD,BD=CE,若∠A=52°,则∠FDE= .
13.如图,在锐角三角形ABC中,∠BAC=60°,BE,CD为三角形ABC的角平分线.BE,CD交于点F,FG平分∠BFC,有下列四个结论:①∠BFC=120°;②BD=BG;③△BDF≌△CEF;④BC=BD+CE.其中结论正确的序号有 .
14.如图,CA⊥BC,垂足为C,AC=3cm,BC=9cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动 秒时,△BCA与点P、N、B为顶点的三角形全等.
三.解答题
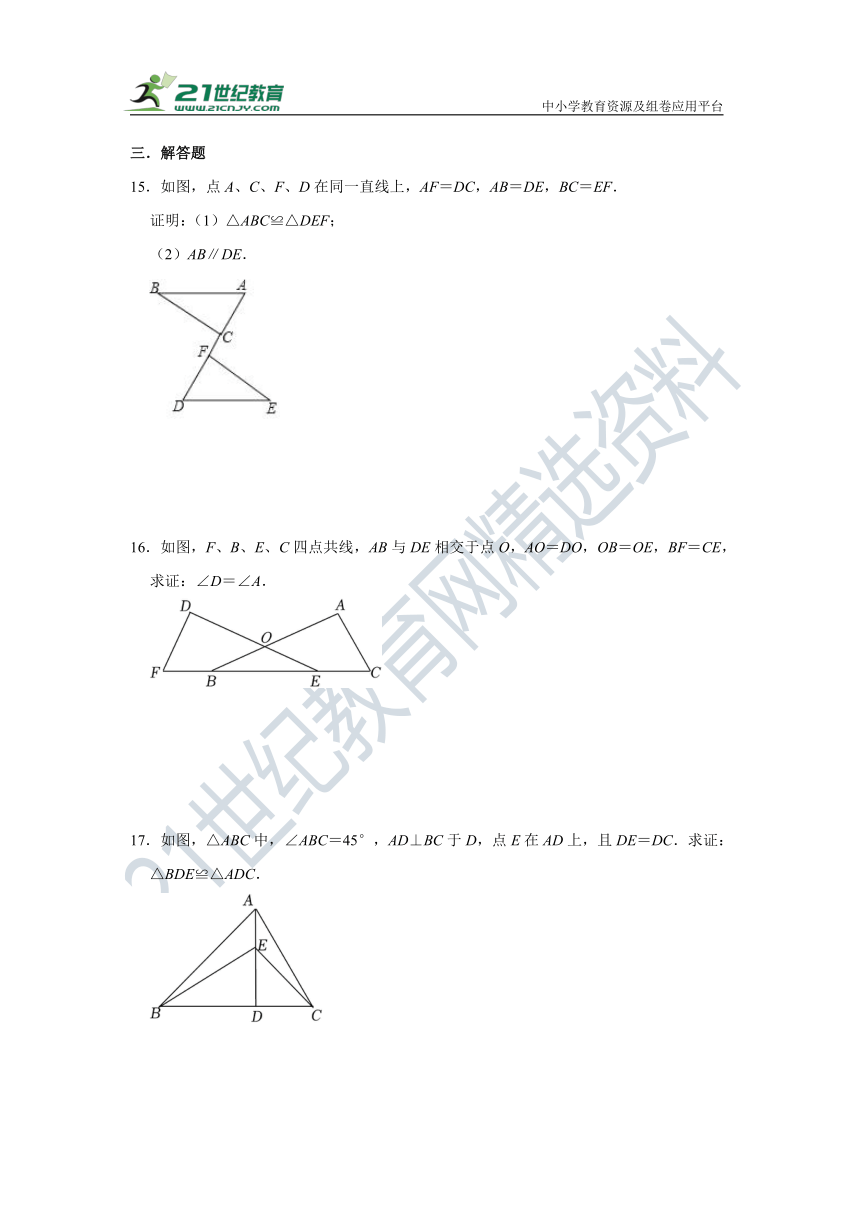
15.如图,点A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF.
证明:(1)△ABC≌△DEF;
(2)AB∥DE.
16.如图,F、B、E、C四点共线,AB与DE相交于点O,AO=DO,OB=OE,BF=CE,求证:∠D=∠A.
17.如图,△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且DE=DC.求证:△BDE≌△ADC.
18.如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠B=70°,求∠C的度数;
(2)若AE=AC.求证:AD平分∠BDE.
19.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB;
(2)若∠BDC=70°,求∠DBC的度数.
20.如图,在△ABC和△AED中,AB=AC,AE=AD,∠BAC=∠EAD,且点E,A,B在同一直线上,点C,D在EB同侧,连结BD,CE交于点M.
(1)求证:△ABD≌△ACE;
(2)若∠CAD=100°,求∠DME的度数.
参考答案
一.选择题
1.【解答】解:∵∠A=180°﹣42°﹣51°=87°,
根据AAS可以判定甲与△ABC全等,根据ASA可以判定乙与△ABC全等.
故选:A.
2.【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
3.【解答】解:A.AB=3,AC=4,∠B=30°,不符合三角形全等的条件,三角形不能唯一作出,所以A选项不符合题意;
B.AB=3,BC=4,AC=8,不符合三角形三边的关系,不能作出三角形,所以B选项不符合题意;
C.∠A=50°,∠B=60°,AB=4,符合三角形全等的条件,三角形能唯一作出,所以C选项符合题意;
D.∠C=90°,AB=5,不符合三角形全等的条件,三角形不能唯一作出,所以D选项不符合题意.
故选:C.
4.【解答】解:∵AB=DE,∠B=∠DEF,
若添加∠A=∠D,则△ABC≌△DEF(ASA),故A不符合题意;
若添加BE=CF,则BC=EF,则△ABC≌△DEF(SAS),故B不符合题意;
若添加AC=DF,则△ABC和△DEF不一定全等,故C符合题意;
若添加AC∥DF,则∠ACB=∠DFE,则△ABC≌△DEF(AAS),故D不符合题意;
故选:C.
5.【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:B.
6.【解答】解:∠ABC+∠DFE=90°,理由如下:
由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°,
故选:C.
7.【解答】解:如图,∵∠1=∠2=110°,
∴180°﹣∠1=180°﹣∠2,
∵∠ADC=∠180°﹣∠1,∠AEB=180°﹣∠2,
∴∠ADC=∠AEB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴∠CAD=∠BAE=60°,
∴∠C=∠1﹣∠CAD=110°﹣60°=50°,
∴∠CAE=180°﹣∠2﹣∠C=180°﹣110°﹣50°=20°,
∴∠CAE的度数为20°,
故选:D.
8.【解答】解:如图,作AF⊥CD于点F,AG⊥BE于点G,则∠AFC=∠AGE=90°,
∵∠DAB=∠CAE=α,
∴∠DAC=∠BAE=α+∠BAC,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴∠ACF=∠AEG,
在△ACF和△AEG中
,
∴△ACF≌△AEG(AAS),
∴AF=AG,
∴点A在∠DPE的平分线上,
∴∠APE=∠APD=∠DPE,
∵∠CPE+∠ACF=∠CAE+∠AEG=∠AHP,
∴∠CPE=∠CAE=α,
∴∠APE=∠DPE=(180°﹣∠CPE)=90°﹣α,
∴∠APC=∠APE+∠CPE=90°﹣α+α=90°+α,
∴∠APC的度数为90°+α,
故选:D.
二.填空题
9.【解答】解:添加条件为BD=CE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SSS),
故答案为:BD=CE(答案不唯一).
10.【解答】解:∵AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,
∴∠C=∠AED=∠BAD=90°,
∴∠B+∠BAC=90°,∠BAC+∠DAE=90°,
∴∠B=∠DAE,
在△ABC和△DAE中,
,
∴△ABC≌△DAE(ASA),
∴AC=DE=7,
∵AE=4,
∴EC=AC﹣AE=7﹣4=3.
故答案为3.
11.【解答】解:∵AD=CB,AB=CD,DB=BD,
∴根据“SSS”可判断△ADB≌△CBD;
∴∠A=∠C,
∵∠AOD=∠COB,AD=BC,
∴根据“AAS”可判断△AOD≌△COB,
综上所述,图中共有2对全等三角形.
故答案为:2.
12.【解答】解:∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠FDB=∠DEC,
∵∠A=52°,∠B=∠C,
∴∠B=∠C==64°,
∵∠BDF+∠EDC+∠FDE=∠C+∠EDC+∠DEC=180°
∴∠FDE=∠C=64°.
故答案为:64°.
13.【解答】解:∵∠A=60°,BE、CD为三角形ABC的角平分线,
∴∠EBC+∠DCB=ABC+ACB=(180°﹣∠A)=60°,
∴∠BFC=180°﹣(∠EBC+∠DCB)=120°,故①正确;
由①得,∠DFB=60°,∠BFC=120°,
∵FG平分∠BFC,
∴∠BFG=BFC=60°,
在△BDF和△BGF中,
,
∴△BDF≌△BGF(ASA),
∴BD=BG,故②正确;
在△BDF和△CEF中,
∠BFD=∠CFE=60°,但没有相等的边,
∴△BDF和△CEF不一定全等,故③错误;
由②可得BD=BG,
同理可得△CEF≌△CGF(ASA),
∴CE=CG,
∴BC=BG+CG=BD+CE,故④正确.
综上所述:结论正确的序号有①②④.
故答案为:①②④.
14.【解答】解:①当P在线段BC上,AC=BP时,△ACB与△PBN全等,
∵AC=3cm,
∴BP=3cm,
∴CP=9﹣3=6cm,
∴点P的运动时间为6÷1=6(秒);
②当P在线段BC上,AC=BN时,△ACB与△NBP全等,
这时BC=PB=9cm,CP=0,因此时间为0秒;
③当P在BQ上,AC=BP时,△ACB与△PBN全等,
∵AC=3cm,
∴BP=3cm,
∴CP=3+9=12cm,
∴点P的运动时间为12÷1=12(秒);
④当P在BQ上,AC=NB时,△ACB与△NBP全等,
∵BC=9cm,
∴BP=9cm,
∴CP=9+9=18,
点P的运动时间为18÷1=18(秒),
故答案为:0或6或12或18.
三.解答题
15.【解答】证明:(1)∵AF=CD,
∴AF﹣FC=CD﹣FC即AC=DF.
∵AB∥DE,
∴∠A=∠D.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
(2)由(1)知△ABC≌△DEF,
∴∠A=∠D,
∴AB∥DE.
16.【解答】证明:∵OB=OE,
∴∠DEF=∠ABC,
∵AO=DO,BF=CE,
∴AO+OB=DO+OE,CE+BE=BF+BE,
∴DE=AB,EF=BC,
在△DEF和△ABC中,
,
∴△DEF≌△ABC(SAS),
∴∠D=∠A.
17.【解答】证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABC=∠BAD,
∴AD=BD,
在△BDE和△ADC中,
,
∴△BDE≌△ADC(SAS).
18.【解答】(1)解:∵AD=AB,∠B=70°,
∴∠B=∠ADB=70°,
∴∠BAD=180°﹣∠B﹣∠ADB=40°,
∴∠BAD=∠CAE=40°,
∵AE∥BC,
∴∠C=∠CAE=40°.
(2)证明:∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,
即∠BAC=∠DAE,
∵在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS),
∴∠B=∠ADE,
∴∠ADB=∠ADE,
∴AD平分∠BDE.
19.【解答】(1)证明:∵AD∥BC,
∴∠ADB=∠EBC,
在△ABD和△ECB中,
,
∴△ABD≌△ECB(ASA);
(2)解:∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°.
20.【解答】(1)证明:∵∠BAC=∠EAD,
∴∠BAC+∠DAC=∠EAD+∠DAC,即∠DAB=∠EAC,
在△EAC和△DAB中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠BAC=∠EAD,∠CAD=100°,
∴∠BAC=∠EAD===40°,
∵∠BAC是△EAC的外角,
∴∠BAC=∠AEC+∠ACE=40°,
∵△ABD≌△ACE,
∴∠ECA=∠DBA,
∵∠DME是△BME的外角,
∴∠DME=∠AEC+∠ABD=∠AEC+∠ACE=40°.
12.2 三角形全等的判定 同步练习卷
一.选择题
1.如图,已知△ABC的三条边和三个角,则甲、乙、丙三个三角形中和△ABC全等的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.只有甲
2.如图,一块玻璃被打碎成三块,如果要去玻璃店配一块完全一样的玻璃,那么最合理的办法是( )
A.带①去 B.带②去 C.带③去 D.带①②③去
3.根据下列条件,能作出唯一的△ABC的是( )
A.AB=3,AC=4,∠B=30° B.AB=3,BC=4,AC=8
C.∠A=50°,∠B=60°,AB=4 D.∠C=90°,AB=5
4.如图,AB=DE,∠B=∠DEF,添加下列哪个条件,不能证明△ABC≌△DEF的是( )
A.∠A=∠D B.BC=EF C.AC=DF D.AC∥DF
5.如图,要测量河两岸相对的两点A,B之间的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长,则上述操作,判定△EDC≌△ABC的理由是( )
A.SSS B.ASA C.AAS D.SAS
6.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A.60° B.75° C.90° D.120°
7.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为( )
A.50° B.60° C.40° D.20°
8.如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( )
A.90°﹣α B.90°+α C.90°﹣α D.90°+α
二.填空题
9.如图,已知AB=AC,AD=AE,要证明△ABD≌△ACE,还需要添加条件为 (只写一种).
10.如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,若BC=AE=4,DE=7,则EC= .
11.已知,如图,AD=CB,AB=CD,那么图中共有 对全等三角形.
12.如图,△ABC中,AB=AC,BF=CD,BD=CE,若∠A=52°,则∠FDE= .
13.如图,在锐角三角形ABC中,∠BAC=60°,BE,CD为三角形ABC的角平分线.BE,CD交于点F,FG平分∠BFC,有下列四个结论:①∠BFC=120°;②BD=BG;③△BDF≌△CEF;④BC=BD+CE.其中结论正确的序号有 .
14.如图,CA⊥BC,垂足为C,AC=3cm,BC=9cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动 秒时,△BCA与点P、N、B为顶点的三角形全等.
三.解答题
15.如图,点A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF.
证明:(1)△ABC≌△DEF;
(2)AB∥DE.
16.如图,F、B、E、C四点共线,AB与DE相交于点O,AO=DO,OB=OE,BF=CE,求证:∠D=∠A.
17.如图,△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且DE=DC.求证:△BDE≌△ADC.
18.如图,在△ABC中,点D是BC上一点,且AD=AB,AE∥BC,∠BAD=∠CAE,连接DE交AC于点F.
(1)若∠B=70°,求∠C的度数;
(2)若AE=AC.求证:AD平分∠BDE.
19.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB;
(2)若∠BDC=70°,求∠DBC的度数.
20.如图,在△ABC和△AED中,AB=AC,AE=AD,∠BAC=∠EAD,且点E,A,B在同一直线上,点C,D在EB同侧,连结BD,CE交于点M.
(1)求证:△ABD≌△ACE;
(2)若∠CAD=100°,求∠DME的度数.
参考答案
一.选择题
1.【解答】解:∵∠A=180°﹣42°﹣51°=87°,
根据AAS可以判定甲与△ABC全等,根据ASA可以判定乙与△ABC全等.
故选:A.
2.【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
3.【解答】解:A.AB=3,AC=4,∠B=30°,不符合三角形全等的条件,三角形不能唯一作出,所以A选项不符合题意;
B.AB=3,BC=4,AC=8,不符合三角形三边的关系,不能作出三角形,所以B选项不符合题意;
C.∠A=50°,∠B=60°,AB=4,符合三角形全等的条件,三角形能唯一作出,所以C选项符合题意;
D.∠C=90°,AB=5,不符合三角形全等的条件,三角形不能唯一作出,所以D选项不符合题意.
故选:C.
4.【解答】解:∵AB=DE,∠B=∠DEF,
若添加∠A=∠D,则△ABC≌△DEF(ASA),故A不符合题意;
若添加BE=CF,则BC=EF,则△ABC≌△DEF(SAS),故B不符合题意;
若添加AC=DF,则△ABC和△DEF不一定全等,故C符合题意;
若添加AC∥DF,则∠ACB=∠DFE,则△ABC≌△DEF(AAS),故D不符合题意;
故选:C.
5.【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:B.
6.【解答】解:∠ABC+∠DFE=90°,理由如下:
由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°,
故选:C.
7.【解答】解:如图,∵∠1=∠2=110°,
∴180°﹣∠1=180°﹣∠2,
∵∠ADC=∠180°﹣∠1,∠AEB=180°﹣∠2,
∴∠ADC=∠AEB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴∠CAD=∠BAE=60°,
∴∠C=∠1﹣∠CAD=110°﹣60°=50°,
∴∠CAE=180°﹣∠2﹣∠C=180°﹣110°﹣50°=20°,
∴∠CAE的度数为20°,
故选:D.
8.【解答】解:如图,作AF⊥CD于点F,AG⊥BE于点G,则∠AFC=∠AGE=90°,
∵∠DAB=∠CAE=α,
∴∠DAC=∠BAE=α+∠BAC,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴∠ACF=∠AEG,
在△ACF和△AEG中
,
∴△ACF≌△AEG(AAS),
∴AF=AG,
∴点A在∠DPE的平分线上,
∴∠APE=∠APD=∠DPE,
∵∠CPE+∠ACF=∠CAE+∠AEG=∠AHP,
∴∠CPE=∠CAE=α,
∴∠APE=∠DPE=(180°﹣∠CPE)=90°﹣α,
∴∠APC=∠APE+∠CPE=90°﹣α+α=90°+α,
∴∠APC的度数为90°+α,
故选:D.
二.填空题
9.【解答】解:添加条件为BD=CE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SSS),
故答案为:BD=CE(答案不唯一).
10.【解答】解:∵AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,
∴∠C=∠AED=∠BAD=90°,
∴∠B+∠BAC=90°,∠BAC+∠DAE=90°,
∴∠B=∠DAE,
在△ABC和△DAE中,
,
∴△ABC≌△DAE(ASA),
∴AC=DE=7,
∵AE=4,
∴EC=AC﹣AE=7﹣4=3.
故答案为3.
11.【解答】解:∵AD=CB,AB=CD,DB=BD,
∴根据“SSS”可判断△ADB≌△CBD;
∴∠A=∠C,
∵∠AOD=∠COB,AD=BC,
∴根据“AAS”可判断△AOD≌△COB,
综上所述,图中共有2对全等三角形.
故答案为:2.
12.【解答】解:∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠FDB=∠DEC,
∵∠A=52°,∠B=∠C,
∴∠B=∠C==64°,
∵∠BDF+∠EDC+∠FDE=∠C+∠EDC+∠DEC=180°
∴∠FDE=∠C=64°.
故答案为:64°.
13.【解答】解:∵∠A=60°,BE、CD为三角形ABC的角平分线,
∴∠EBC+∠DCB=ABC+ACB=(180°﹣∠A)=60°,
∴∠BFC=180°﹣(∠EBC+∠DCB)=120°,故①正确;
由①得,∠DFB=60°,∠BFC=120°,
∵FG平分∠BFC,
∴∠BFG=BFC=60°,
在△BDF和△BGF中,
,
∴△BDF≌△BGF(ASA),
∴BD=BG,故②正确;
在△BDF和△CEF中,
∠BFD=∠CFE=60°,但没有相等的边,
∴△BDF和△CEF不一定全等,故③错误;
由②可得BD=BG,
同理可得△CEF≌△CGF(ASA),
∴CE=CG,
∴BC=BG+CG=BD+CE,故④正确.
综上所述:结论正确的序号有①②④.
故答案为:①②④.
14.【解答】解:①当P在线段BC上,AC=BP时,△ACB与△PBN全等,
∵AC=3cm,
∴BP=3cm,
∴CP=9﹣3=6cm,
∴点P的运动时间为6÷1=6(秒);
②当P在线段BC上,AC=BN时,△ACB与△NBP全等,
这时BC=PB=9cm,CP=0,因此时间为0秒;
③当P在BQ上,AC=BP时,△ACB与△PBN全等,
∵AC=3cm,
∴BP=3cm,
∴CP=3+9=12cm,
∴点P的运动时间为12÷1=12(秒);
④当P在BQ上,AC=NB时,△ACB与△NBP全等,
∵BC=9cm,
∴BP=9cm,
∴CP=9+9=18,
点P的运动时间为18÷1=18(秒),
故答案为:0或6或12或18.
三.解答题
15.【解答】证明:(1)∵AF=CD,
∴AF﹣FC=CD﹣FC即AC=DF.
∵AB∥DE,
∴∠A=∠D.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
(2)由(1)知△ABC≌△DEF,
∴∠A=∠D,
∴AB∥DE.
16.【解答】证明:∵OB=OE,
∴∠DEF=∠ABC,
∵AO=DO,BF=CE,
∴AO+OB=DO+OE,CE+BE=BF+BE,
∴DE=AB,EF=BC,
在△DEF和△ABC中,
,
∴△DEF≌△ABC(SAS),
∴∠D=∠A.
17.【解答】证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABC=∠BAD,
∴AD=BD,
在△BDE和△ADC中,
,
∴△BDE≌△ADC(SAS).
18.【解答】(1)解:∵AD=AB,∠B=70°,
∴∠B=∠ADB=70°,
∴∠BAD=180°﹣∠B﹣∠ADB=40°,
∴∠BAD=∠CAE=40°,
∵AE∥BC,
∴∠C=∠CAE=40°.
(2)证明:∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,
即∠BAC=∠DAE,
∵在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS),
∴∠B=∠ADE,
∴∠ADB=∠ADE,
∴AD平分∠BDE.
19.【解答】(1)证明:∵AD∥BC,
∴∠ADB=∠EBC,
在△ABD和△ECB中,
,
∴△ABD≌△ECB(ASA);
(2)解:∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°.
20.【解答】(1)证明:∵∠BAC=∠EAD,
∴∠BAC+∠DAC=∠EAD+∠DAC,即∠DAB=∠EAC,
在△EAC和△DAB中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠BAC=∠EAD,∠CAD=100°,
∴∠BAC=∠EAD===40°,
∵∠BAC是△EAC的外角,
∴∠BAC=∠AEC+∠ACE=40°,
∵△ABD≌△ACE,
∴∠ECA=∠DBA,
∵∠DME是△BME的外角,
∴∠DME=∠AEC+∠ABD=∠AEC+∠ACE=40°.
