2022年“国庆假期7件套”八年级上册:12.1 全等三角形同步练习(6)(含解析)
文档属性
| 名称 | 2022年“国庆假期7件套”八年级上册:12.1 全等三角形同步练习(6)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 316.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 20:54:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12.1 全等三角形 同步练习
一.选择题
1.下列说法正确的是( )
A.面积相等的两个图形是全等图形
B.全等三角形的周长相等
C.所有正方形都是全等图形
D.全等三角形的边相等
2.如图,△OAB≌△OCD,若∠A=80°,OB=3,则下列说法正确的是( )
A.∠COD=80° B.CD=3 C.∠D=20° D.OD=3
3.如图所示,△ABC≌△AEF,在下列结论中,不正确的是( )
A.∠EAB=∠FAC B.BC=EF
C.∠BAC=∠CAF D.CA 平分∠BCF
4.如图,点B,E,C,F在同一直线上,△ABC≌△DEF,BC=8,BF=11.5,则EC的长为( )
A.5 B.4.5 C.4 D.3.5
5.如图,在四边形ABCD与四边形A'B'C′D'中,AB=A'B',∠B=∠B',BC=B'C'.下列条件中:
①∠A=∠A′,AD=A′D′;
②∠A=∠A',∠D=∠D';
③∠A=∠A',CD=C'D';
④AD=A′D′,CD=C′D′.
添加上述条件中的其中一个,可使四边形ABCD≌四边形A′B′C′D′.上述条件中符合要求的有( )
A.②③ B.①②④ C.①③④ D.①②③④
6.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
二.填空题
7.若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1= °.
8.如图,△ACE≌△DBF,若∠A=66°,∠E=78°,则∠FBD的度数为 .
9.如图,△ABC≌△DBE,AB=6,AC=9,BE=5,则△ABC的周长为 .
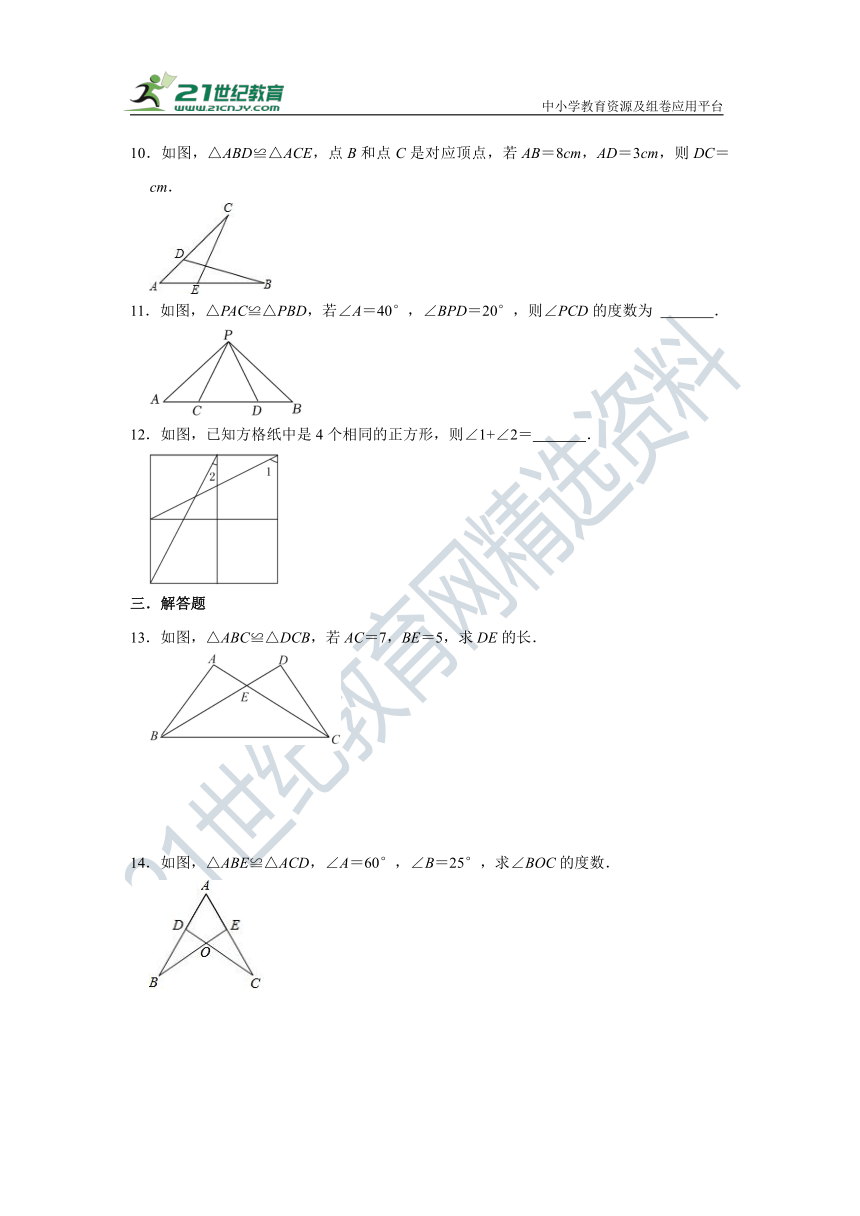
10.如图,△ABD≌△ACE,点B和点C是对应顶点,若AB=8cm,AD=3cm,则DC= cm.
11.如图,△PAC≌△PBD,若∠A=40°,∠BPD=20°,则∠PCD的度数为 .
12.如图,已知方格纸中是4个相同的正方形,则∠1+∠2= .
三.解答题
13.如图,△ABC≌△DCB,若AC=7,BE=5,求DE的长.
14.如图,△ABE≌△ACD,∠A=60°,∠B=25°,求∠BOC的度数.
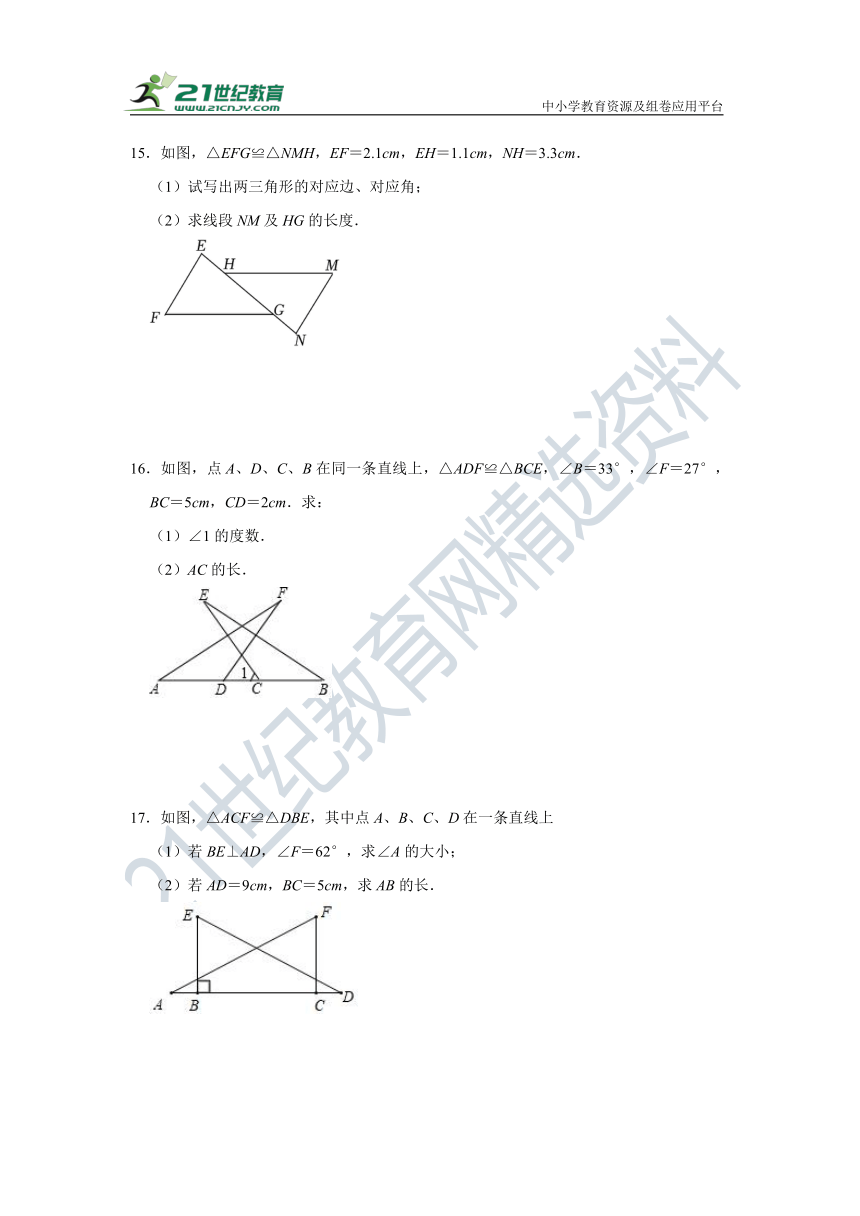
15.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
(2)求线段NM及HG的长度.
16.如图,点A、D、C、B在同一条直线上,△ADF≌△BCE,∠B=33°,∠F=27°,BC=5cm,CD=2cm.求:
(1)∠1的度数.
(2)AC的长.
17.如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上
(1)若BE⊥AD,∠F=62°,求∠A的大小;
(2)若AD=9cm,BC=5cm,求AB的长.
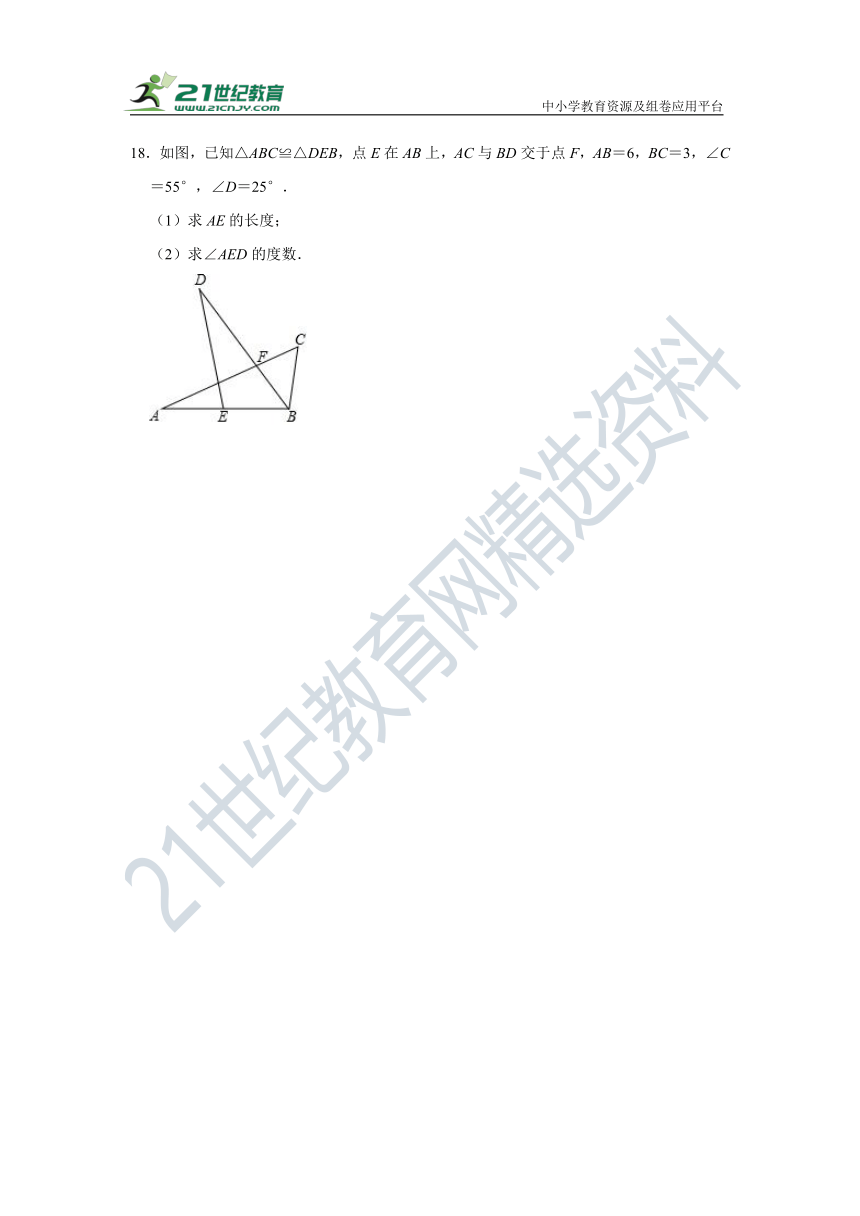
18.如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
参考答案
一.选择题
1.【解答】解:A、面积相等,但图形不一定能完全重合,错不符合题意;
B、全等三角形的周长相等,正确符合题意;
C、正方形的面积不相等,也不是全等形,错不符合题意;
D、全等三角形的对应边相等,错不符合题意.
故选:B.
2.【解答】解:∵△OAB≌△OCD,∠A=80°,OB=3,
∴∠C=∠A=80°,OD=OB=3.
所以选项ABC说法错误,选项D说法正确.
故选:D.
3.【解答】解:∵△ABC≌△AEF,
∴BC=EF,AC=AF,∠B=∠E,∠BAC=∠EAF,∠BCA=∠F,故B正确,不符合题意;C错误,符合题意;
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠EAB=∠FAC,故A正确,不符合题意;
∵AC=AF,
∴∠ACF=∠F,
∴∠BCA=∠ACF,
∴CA平分∠BCF,
故D正确,不符合题意;
故选:C.
4.【解答】解:∵BC=8,BF=11.5,
∴CF=BF﹣BC=3.5,
∵△ABC≌△DEF,BC=8,
∴EF=BC=8,
∴EC=EF﹣CF=8﹣3.5=4.5,
故选:B.
5.【解答】解:符合要求的条件是①②④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,∠ACB=∠A′C′B′,
∵∠BAD=∠B′A′D′,
∴∠BAD﹣∠DAC=∠B′A′D′﹣∠D′A′C′,
∴∠DAC=∠D′A′C′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D′,∠ACD=∠A′C′D′,CD=C′D′,
∴∠BCD=∠B′C′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同理根据②④的条件证得四边形ABCD≌四边形A′B′C′D′.
故选:B.
6.【解答】解:∵∠B=80°,∠C=30°,
∴∠BAC=70°,
∵∠DAC=32°,
∴∠BAD=38°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠EAC=∠BAD=38°,
故选:D.
二.填空题
7.【解答】解:∵∠A=110°,∠B=40°,
∴∠C=180°﹣110°﹣40°=30°,
∵△ABC≌△A1B1C1,
∴∠C1=∠C=30°,
故答案为:30.
8.【解答】解:∵△ACE≌△DBF,∠A=66°,∠E=78°,
∴∠D=∠A=66°,∠F=∠E=78°,
∴∠FBD=180°﹣∠D﹣∠F=36°,
故答案为:36°.
9.【解答】解:∵△ABC≌△DBE,BE=5,
∴BC=BE=5,
∵AB=6,AC=9,
∴△ABC的周长=AB+AC+BC=6+9+5=20.
故答案为:20.
10.【解答】解:∵△ABD≌△ACE,点B和点C是对应顶点,
∴AB=AC=8cm,
∴DC=AC﹣AD=5(cm).
故答案为:5.
11.【解答】解:∵△PAC≌△PBD,∠BPD=20°,
∴∠APC=∠BPD=20°,
∵∠A=40°,
∴∠PCD=∠A+∠APC=40°+20°=60°,
故答案为:60°.
12.【解答】解:如图所示:
由题意可得:△ACB≌△DFE,
则∠1=∠FDE,
∵∠2+∠FDE=90°,
∴∠1+∠2=90°.
故答案为:90°.
三.解答题
13.【解答】解:∵△ABC≌△DCB,
∴DB=AC=7,
∴DE=BD﹣BE=7﹣5=2.
14.【解答】解:∵∠A=60°,∠B=25°,
∴∠CEO=∠A+∠B=85°,
∵△ABE≌△ACD,
∴∠B=∠C=25°,
∴∠BOC=∠C+∠CEO=110°.
15.【解答】解:(1)∵△EFG≌△NMH,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵EG=NH,EH+HG=EG,EH=1.1cm,HN=3.3cm,
∴HG=EG﹣EH=HN﹣EH=3.3﹣1.1=2.2(cm).
16.【解答】解:(1)∵△ADF≌△BCE,∠F=27°,
∴∠E=∠F=27°,
∵∠1=∠B+∠E,∠B=33°,
∴∠1=60°;
(2)∵△ADF≌△BCE,BC=5cm,
∴AD=BC=5cm,
∵CD=2cm,
∴AC=AD+CD=7cm.
17.【解答】解:(1)∵BE⊥AD,
∴∠EBD=90°,
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°﹣∠F=28°;
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA﹣CB=BD﹣BC,即AB=CD,
∵AD=9cm,BC=5cm,
∴AB+CD=9﹣5=4cm,
∴AB=2cm.
18.【解答】解:(1)∵△ABC≌△DEB,
∴BE=BC=3,
∴AE=AB﹣BE=6﹣3=3;
(2)∵△ABC≌△DEB,
∴∠A=∠D=25°,∠DBE=∠C=55°,
∴∠AED=∠DBE+∠D=25°+55°=80°.
12.1 全等三角形 同步练习
一.选择题
1.下列说法正确的是( )
A.面积相等的两个图形是全等图形
B.全等三角形的周长相等
C.所有正方形都是全等图形
D.全等三角形的边相等
2.如图,△OAB≌△OCD,若∠A=80°,OB=3,则下列说法正确的是( )
A.∠COD=80° B.CD=3 C.∠D=20° D.OD=3
3.如图所示,△ABC≌△AEF,在下列结论中,不正确的是( )
A.∠EAB=∠FAC B.BC=EF
C.∠BAC=∠CAF D.CA 平分∠BCF
4.如图,点B,E,C,F在同一直线上,△ABC≌△DEF,BC=8,BF=11.5,则EC的长为( )
A.5 B.4.5 C.4 D.3.5
5.如图,在四边形ABCD与四边形A'B'C′D'中,AB=A'B',∠B=∠B',BC=B'C'.下列条件中:
①∠A=∠A′,AD=A′D′;
②∠A=∠A',∠D=∠D';
③∠A=∠A',CD=C'D';
④AD=A′D′,CD=C′D′.
添加上述条件中的其中一个,可使四边形ABCD≌四边形A′B′C′D′.上述条件中符合要求的有( )
A.②③ B.①②④ C.①③④ D.①②③④
6.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
二.填空题
7.若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1= °.
8.如图,△ACE≌△DBF,若∠A=66°,∠E=78°,则∠FBD的度数为 .
9.如图,△ABC≌△DBE,AB=6,AC=9,BE=5,则△ABC的周长为 .
10.如图,△ABD≌△ACE,点B和点C是对应顶点,若AB=8cm,AD=3cm,则DC= cm.
11.如图,△PAC≌△PBD,若∠A=40°,∠BPD=20°,则∠PCD的度数为 .
12.如图,已知方格纸中是4个相同的正方形,则∠1+∠2= .
三.解答题
13.如图,△ABC≌△DCB,若AC=7,BE=5,求DE的长.
14.如图,△ABE≌△ACD,∠A=60°,∠B=25°,求∠BOC的度数.
15.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
(2)求线段NM及HG的长度.
16.如图,点A、D、C、B在同一条直线上,△ADF≌△BCE,∠B=33°,∠F=27°,BC=5cm,CD=2cm.求:
(1)∠1的度数.
(2)AC的长.
17.如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上
(1)若BE⊥AD,∠F=62°,求∠A的大小;
(2)若AD=9cm,BC=5cm,求AB的长.
18.如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
参考答案
一.选择题
1.【解答】解:A、面积相等,但图形不一定能完全重合,错不符合题意;
B、全等三角形的周长相等,正确符合题意;
C、正方形的面积不相等,也不是全等形,错不符合题意;
D、全等三角形的对应边相等,错不符合题意.
故选:B.
2.【解答】解:∵△OAB≌△OCD,∠A=80°,OB=3,
∴∠C=∠A=80°,OD=OB=3.
所以选项ABC说法错误,选项D说法正确.
故选:D.
3.【解答】解:∵△ABC≌△AEF,
∴BC=EF,AC=AF,∠B=∠E,∠BAC=∠EAF,∠BCA=∠F,故B正确,不符合题意;C错误,符合题意;
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠EAB=∠FAC,故A正确,不符合题意;
∵AC=AF,
∴∠ACF=∠F,
∴∠BCA=∠ACF,
∴CA平分∠BCF,
故D正确,不符合题意;
故选:C.
4.【解答】解:∵BC=8,BF=11.5,
∴CF=BF﹣BC=3.5,
∵△ABC≌△DEF,BC=8,
∴EF=BC=8,
∴EC=EF﹣CF=8﹣3.5=4.5,
故选:B.
5.【解答】解:符合要求的条件是①②④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,∠ACB=∠A′C′B′,
∵∠BAD=∠B′A′D′,
∴∠BAD﹣∠DAC=∠B′A′D′﹣∠D′A′C′,
∴∠DAC=∠D′A′C′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D′,∠ACD=∠A′C′D′,CD=C′D′,
∴∠BCD=∠B′C′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同理根据②④的条件证得四边形ABCD≌四边形A′B′C′D′.
故选:B.
6.【解答】解:∵∠B=80°,∠C=30°,
∴∠BAC=70°,
∵∠DAC=32°,
∴∠BAD=38°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠EAC=∠BAD=38°,
故选:D.
二.填空题
7.【解答】解:∵∠A=110°,∠B=40°,
∴∠C=180°﹣110°﹣40°=30°,
∵△ABC≌△A1B1C1,
∴∠C1=∠C=30°,
故答案为:30.
8.【解答】解:∵△ACE≌△DBF,∠A=66°,∠E=78°,
∴∠D=∠A=66°,∠F=∠E=78°,
∴∠FBD=180°﹣∠D﹣∠F=36°,
故答案为:36°.
9.【解答】解:∵△ABC≌△DBE,BE=5,
∴BC=BE=5,
∵AB=6,AC=9,
∴△ABC的周长=AB+AC+BC=6+9+5=20.
故答案为:20.
10.【解答】解:∵△ABD≌△ACE,点B和点C是对应顶点,
∴AB=AC=8cm,
∴DC=AC﹣AD=5(cm).
故答案为:5.
11.【解答】解:∵△PAC≌△PBD,∠BPD=20°,
∴∠APC=∠BPD=20°,
∵∠A=40°,
∴∠PCD=∠A+∠APC=40°+20°=60°,
故答案为:60°.
12.【解答】解:如图所示:
由题意可得:△ACB≌△DFE,
则∠1=∠FDE,
∵∠2+∠FDE=90°,
∴∠1+∠2=90°.
故答案为:90°.
三.解答题
13.【解答】解:∵△ABC≌△DCB,
∴DB=AC=7,
∴DE=BD﹣BE=7﹣5=2.
14.【解答】解:∵∠A=60°,∠B=25°,
∴∠CEO=∠A+∠B=85°,
∵△ABE≌△ACD,
∴∠B=∠C=25°,
∴∠BOC=∠C+∠CEO=110°.
15.【解答】解:(1)∵△EFG≌△NMH,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵EG=NH,EH+HG=EG,EH=1.1cm,HN=3.3cm,
∴HG=EG﹣EH=HN﹣EH=3.3﹣1.1=2.2(cm).
16.【解答】解:(1)∵△ADF≌△BCE,∠F=27°,
∴∠E=∠F=27°,
∵∠1=∠B+∠E,∠B=33°,
∴∠1=60°;
(2)∵△ADF≌△BCE,BC=5cm,
∴AD=BC=5cm,
∵CD=2cm,
∴AC=AD+CD=7cm.
17.【解答】解:(1)∵BE⊥AD,
∴∠EBD=90°,
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°﹣∠F=28°;
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA﹣CB=BD﹣BC,即AB=CD,
∵AD=9cm,BC=5cm,
∴AB+CD=9﹣5=4cm,
∴AB=2cm.
18.【解答】解:(1)∵△ABC≌△DEB,
∴BE=BC=3,
∴AE=AB﹣BE=6﹣3=3;
(2)∵△ABC≌△DEB,
∴∠A=∠D=25°,∠DBE=∠C=55°,
∴∠AED=∠DBE+∠D=25°+55°=80°.
