京改版八年级数学上册 第十三章事件与可能性素养综合测试 (含解析)
文档属性
| 名称 | 京改版八年级数学上册 第十三章事件与可能性素养综合测试 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 158.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 13:51:46 | ||
图片预览




文档简介
2022-2023学年度北京课改版版八年级数学上册
素养综合检测
第十三章 事件与可能性
一、选择题(每小题3分,共30分)
1.(2021浙江湖州中考)下列事件中,属于不可能事件的是( )
A.经过红绿灯路口,遇到绿灯
B.射击运动员射击一次,命中靶心
C.班里的两名同学,他们的生日是同一天
D.从一个只装有白球和红球的袋中摸球,摸出黄球
2.(2021湖北襄阳中考)一个不透明的袋子中装有除颜色外完全相同的2个红球和1个白球,从袋子中随机摸出2个球,下列事件是必然事件的是( )
A.摸出的2个球中至少有1个红球
B.摸出的2个球都是白球
C.摸出的2个球中1个红球、1个白球
D.摸出的2个球都是红球
3. 同时投掷两枚质地均匀的骰子(每个骰子的六个面上分别刻有点数1,2,3,…,6),设两枚骰子向上一面的点数之和为S,则下列事件属于随机事件的是( )
A.S=6 B.S>13 C.S=1 D.S>1
4.下列说法正确的是( )
A.在某次足球比赛中,意大利男足战胜德国男足是随机事件
B.任意掷一枚质地均匀的骰子,朝上一面的点数是偶数是必然事件
C.购买一张体育彩票中奖是不可能事件
D.抛掷一枚质地均匀的硬币正面朝上是必然事件
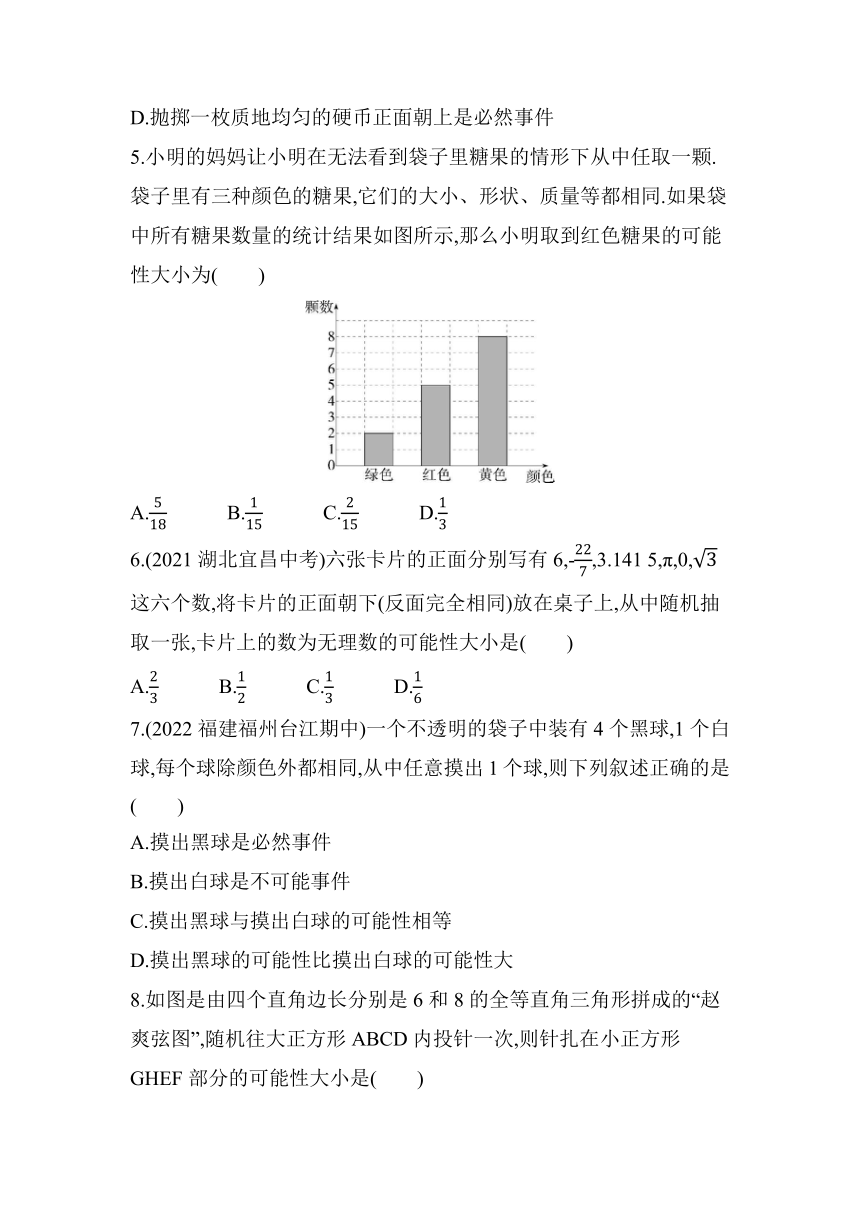
5.小明的妈妈让小明在无法看到袋子里糖果的情形下从中任取一颗.袋子里有三种颜色的糖果,它们的大小、形状、质量等都相同.如果袋中所有糖果数量的统计结果如图所示,那么小明取到红色糖果的可能性大小为( )
A. B. C. D.
6.(2021湖北宜昌中考)六张卡片的正面分别写有6,-,3.141 5,π,0,这六个数,将卡片的正面朝下(反面完全相同)放在桌子上,从中随机抽取一张,卡片上的数为无理数的可能性大小是( )
A. B. C. D.
7.(2022福建福州台江期中)一个不透明的袋子中装有4个黑球,1个白球,每个球除颜色外都相同,从中任意摸出1个球,则下列叙述正确的是( )
A.摸出黑球是必然事件
B.摸出白球是不可能事件
C.摸出黑球与摸出白球的可能性相等
D.摸出黑球的可能性比摸出白球的可能性大
8.如图是由四个直角边长分别是6和8的全等直角三角形拼成的“赵爽弦图”,随机往大正方形ABCD内投针一次,则针扎在小正方形GHEF部分的可能性大小是( )
A. B.C. D.
9.如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个格点中任取一点C,使△ABC为直角三角形的可能性大小是( )
A. B. C. D.
10.若自然数n使三个数的加法运算“n+(n+1)+(n+2)”产生进位现象,则称n为“连加进位数”.例如,2不是“连加进位数”,因为2+3+4=9不产生进位现象;4是“连加进位数”,因为4+5+6=15产生进位现象;51是“连加进位数”,因为51+52+53=156产生进位现象.如果从0,1,…,99这100个数中任取一个数,那么取到“连加进位数”的可能性大小是( )
A.0.88 B.0.89 C.0.90 D.0.91
二、填空题(每小题3分,共24分)
11.“任意画一个四边形,其内角和是360°”是 事件(填“随机”“必然”或“不可能”).
12.口袋中有黄、白、红三种颜色的球各1个,这3个球除颜色外没有其他区别,从口袋中任取1个球,写出一个随机事件: .
13.(2022独家原创)抛掷一枚质地均匀的硬币,正面向上的可能性大小是,第一次的结果是正面向上,再抛掷一次正面向上的可能性大小 (填“>”“<”或“=”).
14.(2021辽宁朝阳中考)如图,一块飞镖游戏板由大小相等的9个小等边三角形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),则飞镖落在阴影区域的可能性大小为 .
15.(2022上海浦东新区期末)在20以内的素数中,随机抽取一个素数,则所抽取的素数是偶数的可能性大小是 .
16.在3□2□(-2)的两个□中,任意填上“+”或“-”,则运算结果为3的可能性大小是 .
17.(2021广西河池中考)从-2,4,5这3个数中,任取两个数作为点P的横、纵坐标,则点P在第四象限的可能性大小是 .
18.(2022北京通州期末)有两个质地均匀的正方体积木,如图所示.
小怡投掷某块积木200次的结果统计如下表:
灰色的面朝上 白色的面朝上
32次 168次
根据表中的数据推测,小怡最有可能投掷的是 号积木(填“①”或“②”).
三、解答题(共46分)
19.(6分)盒中有6个乒乓球,其中2个次品,4个正品,正品和次品大小、形状完全相同,任意从盒中取出3个,出现了下列事件:
(1)3个正品;(2)至少有1个次品;
(3)3个次品;(4)至少有1个正品.
指出这些事件分别是什么事件.
20.(6分)下列事件中,哪些是随机事件 哪些是必然事件 哪些是不可能事件
(1)随意写一个有理数,则其平方大于它本身;
(2)随意写一个有理数,则其平方不小于它本身;
(3)随意写两个不相等的有理数,则它们的平方的和为正数;
(4)随意写两个不同的有理数,则它们和的平方为正数;
(5)四个连续自然数相加,和为奇数;
(6)三个有理数相乘时,若有一个是负数,则它们的积一定是负数.
21.(2021江苏镇江中考改编)(8分)甲、乙、丙三人各自随机选择到A,B两个献血站进行爱心献血.求这三人在同一个献血站献血的可能性大小.
22.(8分)一个口袋中放着若干个黄球和绿球,这两种球除了颜色之外没有其他区别,袋中的球已经搅匀,从口袋中取出一个球是黄球的可能性大小为.
(1)从口袋中随机取出一个球是绿球的可能性大小是多少
(2)如果口袋中的黄球有12个,那么口袋中的绿球有多少个
23.(8分)汉字是世界上最古老的文字之一,字形结构体现了人类追求对称、和谐的天性.如图,这三个汉字可以看成轴对称图形.
(1)请在方框中再写出两个可看成轴对称图形的汉字;
(2)小敏和小慧利用“土”“口”“木”这三个汉字设计了一个游戏,规则如下:将这三个汉字分别写在相同的三张卡片的正面上,背面朝上洗匀后随机抽出一张,记录卡片正面的汉字后,放回洗匀,再随机抽出一张.若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”),则小敏获胜,否则小慧获胜.你认为这个游戏公平吗 为什么
24.(10分)小明选择一家酒店订春节团圆饭.他借助网络评价,选择了A、B、C三家酒店,对每家酒店随机选择1 000条网络评价统计如下:
评价条数等级酒店 五星 四星 三星及 三星以下 合计
A 412 388 x 1 000
B 420 390 190 1 000
C 405 375 220 1 000
(1)求x的值.
(2)当客户给出的评价不低于四星时,称客户获得良好用餐体验.
①请你为小明从A、B、C三家酒店中推荐一家酒店,使能获得良好用餐体验的可能性最大.写出你推荐的结果,并说明理由;
②如果小明选择了你推荐的酒店,一定能够获得良好用餐体验吗
答案全解全析
1.D A、B、C是随机事件,D是不可能事件.
2.A A是必然事件,B是不可能事件,C、D是随机事件.
3.A A是随机事件,B、C是不可能事件,D是必然事件.
4.A A.在某次足球比赛中,意大利男足战胜德国男足是随机事件,本选项说法正确;
B.任意掷一枚质地均匀的骰子,朝上一面的点数是偶数是随机事件,本选项说法错误;
C.购买一张体育彩票中奖是随机事件,本选项说法错误;
D.抛掷一枚质地均匀的硬币正面朝上是随机事件,本选项说法错误.故选A.
5.D 根据题图得绿色糖果的颗数为2,红色糖果的颗数为5,黄色糖果的颗数为8,所以小明取到红色糖果的可能性大小为=.故选D.
6.C ∵六张卡片上分别写有6,-,3.141 5,π,0,这六个数,其中是无理数的是π,,
∴从中随机抽取一张,卡片上的数为无理数的可能性大小为=.
7.D ∵不透明的袋子中装有4个黑球,1个白球,共5个球,
∴摸出黑球的可能性大小是,摸出白球的可能性大小是,
∴摸出黑球的可能性比摸出白球的可能性大.
8.D 由题可知,AB==10,所以大正方形的面积=102=100,小正方形的面积=102-4××6×8=4,所以针扎在小正方形GHEF部分的可能性大小==.
9.D 如图,在余下的7个格点中,能使△ABC为直角三角形的有C2、C4、C5、C6四个点,故在余下的7个格点中任取一点C,使△ABC为直角三角形的可能性大小是,故选D.
10.A 个位进位到十位时,由n+(n+1)+(n+2)≥10得n≥2,所以满足条件的一位数有3,4,5,6,7,8,9,共7个数;从十位进位到百位时,由n+(n+1)+(n+2)≥100得n≥32,所以满足条件的两位数有33,34,35,…,99,共67个数;由“连加进位数”的定义可知,如15+16+17=(10+5)+(10+6)+(10+7)=30+(5+6+7)=30+18=48,即十位与十位相加,个位与个位相加只要出现进位现象的数就是“连加进位数”,所以在10到32之间的13,14,15,16,17,18,19,23,24,25,26,27,28,29也是“连加进位数”,共14个数.综上可知,在0,1,2,…,99这100个数中,“连加进位数”共有88个,所以从这100个数中任意取一个数为“连加进位数”的可能性大小为=0.88.故选A.
11.必然
解析 因为任意一个四边形的内角和为360°,所以任意画一个四边形,其内角和是360°是必然事件.
12.取出一个黄色球(答案不唯一)
解析 从口袋中任取1个球,共有三种情况:取出一个黄色球;取出一个白色球;取出一个红色球.任选一个即可.
13.=
解析 抛掷一枚质地均匀的硬币,正面向上的可能性大小是,所以无论是第几次抛掷,正面向上的可能性大小都是.
14.
解析 ∵总面积为9个小等边三角形的面积,其中阴影区域的面积为3个小等边三角形的面积,∴飞镖落在阴影区域的可能性大小为=.
15.
解析 20以内的素数有8个,这8个素数中偶数有1个,则所抽取的素数是偶数的可能性大小是.
16.
解析 在两个□中,任意填上“+”或“-”,有四种情况,其中有两种情况可使运算结果为3,故运算结果为3的可能性大小是=.
17.
解析 点P的坐标共有6种等可能的情况,它们是(-2,4),(-2,5),(4,-2),(4,5),(5,4),(5,-2),其中点P在第四象限的情况有2种,即(4,-2),(5,-2),所以点P在第四象限的可能性大小为=.
18.②
解析 ①号积木由于三面灰色,三面白色,因此随机投掷1次,朝上的面是白色、灰色的可能性大小都是=50%;②号积木由于一面灰色,五面白色,因此随机投掷1次,朝上的面是灰色的可能性大小是≈16.7%,朝上的面是白色的可能性大小为≈83.3%,由表格中的数据可得,小怡投掷200次积木得到朝上的面为灰色的次数为32,白色的次数为168,∵=16%,接近16.7%,=84%,接近83.3%,故小怡可能投掷的是②号积木.
19.解析 (1),(2)可能发生,也可能不发生,是随机事件.
(3)一定不会发生,是不可能事件.
(4)一定发生,是必然事件.
20.解析 (1)(2)(4)(6)是随机事件.(3)是必然事件.(5)是不可能事件.
21.解析 如果把甲、乙、丙都选择在A献血站献血记为(A,A,A),那么所有的献血选择可以记为(A,A,A),(A,A,B),(A,B,A),(B,A,A),(A,B,B),(B,A,B),(B,B,A),(B,B,B),共8种等可能情况,其中这三人在同一个献血站献血有2种情况,所以这三人在同一个献血站献血的可能性大小为=.
22.解析 (1)P(取出绿球)=1-P(取出黄球)=1-=.
(2)设口袋中的绿球有x个.
根据题意,得=,解得x=18,
经检验,x=18是所列分式方程的解,并且符合实际问题的意义.
答:口袋中的绿球有18个.
23.解析 (1)答案不唯一,如:田、日.
(2)这个游戏不公平.理由:可能出现的结果共有9种,每种结果出现的可能性相等,其中能组成上下结构的汉字的结果有4种:(土,土)“圭”,(口,口)“吕”,(木,口)“杏”,(口,木)“呆”,所以P(小敏获胜)=,P(小慧获胜)=,因为<,所以游戏不公平.
24.解析 (1)x=1 000-412-388=200.
(2)①推荐小明选择B酒店.理由:选择A酒店获得良好用餐体验的可能性大小为=0.8;选择B酒店获得良好用餐体验的可能性大小为=0.81;选择C酒店获得良好用餐体验的可能性大小为=0.78.
∵0.81>0.8>0.78,
∴选择B酒店获得良好用餐体验的可能性最大.
②不一定.
素养综合检测
第十三章 事件与可能性
一、选择题(每小题3分,共30分)
1.(2021浙江湖州中考)下列事件中,属于不可能事件的是( )
A.经过红绿灯路口,遇到绿灯
B.射击运动员射击一次,命中靶心
C.班里的两名同学,他们的生日是同一天
D.从一个只装有白球和红球的袋中摸球,摸出黄球
2.(2021湖北襄阳中考)一个不透明的袋子中装有除颜色外完全相同的2个红球和1个白球,从袋子中随机摸出2个球,下列事件是必然事件的是( )
A.摸出的2个球中至少有1个红球
B.摸出的2个球都是白球
C.摸出的2个球中1个红球、1个白球
D.摸出的2个球都是红球
3. 同时投掷两枚质地均匀的骰子(每个骰子的六个面上分别刻有点数1,2,3,…,6),设两枚骰子向上一面的点数之和为S,则下列事件属于随机事件的是( )
A.S=6 B.S>13 C.S=1 D.S>1
4.下列说法正确的是( )
A.在某次足球比赛中,意大利男足战胜德国男足是随机事件
B.任意掷一枚质地均匀的骰子,朝上一面的点数是偶数是必然事件
C.购买一张体育彩票中奖是不可能事件
D.抛掷一枚质地均匀的硬币正面朝上是必然事件
5.小明的妈妈让小明在无法看到袋子里糖果的情形下从中任取一颗.袋子里有三种颜色的糖果,它们的大小、形状、质量等都相同.如果袋中所有糖果数量的统计结果如图所示,那么小明取到红色糖果的可能性大小为( )
A. B. C. D.
6.(2021湖北宜昌中考)六张卡片的正面分别写有6,-,3.141 5,π,0,这六个数,将卡片的正面朝下(反面完全相同)放在桌子上,从中随机抽取一张,卡片上的数为无理数的可能性大小是( )
A. B. C. D.
7.(2022福建福州台江期中)一个不透明的袋子中装有4个黑球,1个白球,每个球除颜色外都相同,从中任意摸出1个球,则下列叙述正确的是( )
A.摸出黑球是必然事件
B.摸出白球是不可能事件
C.摸出黑球与摸出白球的可能性相等
D.摸出黑球的可能性比摸出白球的可能性大
8.如图是由四个直角边长分别是6和8的全等直角三角形拼成的“赵爽弦图”,随机往大正方形ABCD内投针一次,则针扎在小正方形GHEF部分的可能性大小是( )
A. B.C. D.
9.如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个格点中任取一点C,使△ABC为直角三角形的可能性大小是( )
A. B. C. D.
10.若自然数n使三个数的加法运算“n+(n+1)+(n+2)”产生进位现象,则称n为“连加进位数”.例如,2不是“连加进位数”,因为2+3+4=9不产生进位现象;4是“连加进位数”,因为4+5+6=15产生进位现象;51是“连加进位数”,因为51+52+53=156产生进位现象.如果从0,1,…,99这100个数中任取一个数,那么取到“连加进位数”的可能性大小是( )
A.0.88 B.0.89 C.0.90 D.0.91
二、填空题(每小题3分,共24分)
11.“任意画一个四边形,其内角和是360°”是 事件(填“随机”“必然”或“不可能”).
12.口袋中有黄、白、红三种颜色的球各1个,这3个球除颜色外没有其他区别,从口袋中任取1个球,写出一个随机事件: .
13.(2022独家原创)抛掷一枚质地均匀的硬币,正面向上的可能性大小是,第一次的结果是正面向上,再抛掷一次正面向上的可能性大小 (填“>”“<”或“=”).
14.(2021辽宁朝阳中考)如图,一块飞镖游戏板由大小相等的9个小等边三角形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),则飞镖落在阴影区域的可能性大小为 .
15.(2022上海浦东新区期末)在20以内的素数中,随机抽取一个素数,则所抽取的素数是偶数的可能性大小是 .
16.在3□2□(-2)的两个□中,任意填上“+”或“-”,则运算结果为3的可能性大小是 .
17.(2021广西河池中考)从-2,4,5这3个数中,任取两个数作为点P的横、纵坐标,则点P在第四象限的可能性大小是 .
18.(2022北京通州期末)有两个质地均匀的正方体积木,如图所示.
小怡投掷某块积木200次的结果统计如下表:
灰色的面朝上 白色的面朝上
32次 168次
根据表中的数据推测,小怡最有可能投掷的是 号积木(填“①”或“②”).
三、解答题(共46分)
19.(6分)盒中有6个乒乓球,其中2个次品,4个正品,正品和次品大小、形状完全相同,任意从盒中取出3个,出现了下列事件:
(1)3个正品;(2)至少有1个次品;
(3)3个次品;(4)至少有1个正品.
指出这些事件分别是什么事件.
20.(6分)下列事件中,哪些是随机事件 哪些是必然事件 哪些是不可能事件
(1)随意写一个有理数,则其平方大于它本身;
(2)随意写一个有理数,则其平方不小于它本身;
(3)随意写两个不相等的有理数,则它们的平方的和为正数;
(4)随意写两个不同的有理数,则它们和的平方为正数;
(5)四个连续自然数相加,和为奇数;
(6)三个有理数相乘时,若有一个是负数,则它们的积一定是负数.
21.(2021江苏镇江中考改编)(8分)甲、乙、丙三人各自随机选择到A,B两个献血站进行爱心献血.求这三人在同一个献血站献血的可能性大小.
22.(8分)一个口袋中放着若干个黄球和绿球,这两种球除了颜色之外没有其他区别,袋中的球已经搅匀,从口袋中取出一个球是黄球的可能性大小为.
(1)从口袋中随机取出一个球是绿球的可能性大小是多少
(2)如果口袋中的黄球有12个,那么口袋中的绿球有多少个
23.(8分)汉字是世界上最古老的文字之一,字形结构体现了人类追求对称、和谐的天性.如图,这三个汉字可以看成轴对称图形.
(1)请在方框中再写出两个可看成轴对称图形的汉字;
(2)小敏和小慧利用“土”“口”“木”这三个汉字设计了一个游戏,规则如下:将这三个汉字分别写在相同的三张卡片的正面上,背面朝上洗匀后随机抽出一张,记录卡片正面的汉字后,放回洗匀,再随机抽出一张.若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”),则小敏获胜,否则小慧获胜.你认为这个游戏公平吗 为什么
24.(10分)小明选择一家酒店订春节团圆饭.他借助网络评价,选择了A、B、C三家酒店,对每家酒店随机选择1 000条网络评价统计如下:
评价条数等级酒店 五星 四星 三星及 三星以下 合计
A 412 388 x 1 000
B 420 390 190 1 000
C 405 375 220 1 000
(1)求x的值.
(2)当客户给出的评价不低于四星时,称客户获得良好用餐体验.
①请你为小明从A、B、C三家酒店中推荐一家酒店,使能获得良好用餐体验的可能性最大.写出你推荐的结果,并说明理由;
②如果小明选择了你推荐的酒店,一定能够获得良好用餐体验吗
答案全解全析
1.D A、B、C是随机事件,D是不可能事件.
2.A A是必然事件,B是不可能事件,C、D是随机事件.
3.A A是随机事件,B、C是不可能事件,D是必然事件.
4.A A.在某次足球比赛中,意大利男足战胜德国男足是随机事件,本选项说法正确;
B.任意掷一枚质地均匀的骰子,朝上一面的点数是偶数是随机事件,本选项说法错误;
C.购买一张体育彩票中奖是随机事件,本选项说法错误;
D.抛掷一枚质地均匀的硬币正面朝上是随机事件,本选项说法错误.故选A.
5.D 根据题图得绿色糖果的颗数为2,红色糖果的颗数为5,黄色糖果的颗数为8,所以小明取到红色糖果的可能性大小为=.故选D.
6.C ∵六张卡片上分别写有6,-,3.141 5,π,0,这六个数,其中是无理数的是π,,
∴从中随机抽取一张,卡片上的数为无理数的可能性大小为=.
7.D ∵不透明的袋子中装有4个黑球,1个白球,共5个球,
∴摸出黑球的可能性大小是,摸出白球的可能性大小是,
∴摸出黑球的可能性比摸出白球的可能性大.
8.D 由题可知,AB==10,所以大正方形的面积=102=100,小正方形的面积=102-4××6×8=4,所以针扎在小正方形GHEF部分的可能性大小==.
9.D 如图,在余下的7个格点中,能使△ABC为直角三角形的有C2、C4、C5、C6四个点,故在余下的7个格点中任取一点C,使△ABC为直角三角形的可能性大小是,故选D.
10.A 个位进位到十位时,由n+(n+1)+(n+2)≥10得n≥2,所以满足条件的一位数有3,4,5,6,7,8,9,共7个数;从十位进位到百位时,由n+(n+1)+(n+2)≥100得n≥32,所以满足条件的两位数有33,34,35,…,99,共67个数;由“连加进位数”的定义可知,如15+16+17=(10+5)+(10+6)+(10+7)=30+(5+6+7)=30+18=48,即十位与十位相加,个位与个位相加只要出现进位现象的数就是“连加进位数”,所以在10到32之间的13,14,15,16,17,18,19,23,24,25,26,27,28,29也是“连加进位数”,共14个数.综上可知,在0,1,2,…,99这100个数中,“连加进位数”共有88个,所以从这100个数中任意取一个数为“连加进位数”的可能性大小为=0.88.故选A.
11.必然
解析 因为任意一个四边形的内角和为360°,所以任意画一个四边形,其内角和是360°是必然事件.
12.取出一个黄色球(答案不唯一)
解析 从口袋中任取1个球,共有三种情况:取出一个黄色球;取出一个白色球;取出一个红色球.任选一个即可.
13.=
解析 抛掷一枚质地均匀的硬币,正面向上的可能性大小是,所以无论是第几次抛掷,正面向上的可能性大小都是.
14.
解析 ∵总面积为9个小等边三角形的面积,其中阴影区域的面积为3个小等边三角形的面积,∴飞镖落在阴影区域的可能性大小为=.
15.
解析 20以内的素数有8个,这8个素数中偶数有1个,则所抽取的素数是偶数的可能性大小是.
16.
解析 在两个□中,任意填上“+”或“-”,有四种情况,其中有两种情况可使运算结果为3,故运算结果为3的可能性大小是=.
17.
解析 点P的坐标共有6种等可能的情况,它们是(-2,4),(-2,5),(4,-2),(4,5),(5,4),(5,-2),其中点P在第四象限的情况有2种,即(4,-2),(5,-2),所以点P在第四象限的可能性大小为=.
18.②
解析 ①号积木由于三面灰色,三面白色,因此随机投掷1次,朝上的面是白色、灰色的可能性大小都是=50%;②号积木由于一面灰色,五面白色,因此随机投掷1次,朝上的面是灰色的可能性大小是≈16.7%,朝上的面是白色的可能性大小为≈83.3%,由表格中的数据可得,小怡投掷200次积木得到朝上的面为灰色的次数为32,白色的次数为168,∵=16%,接近16.7%,=84%,接近83.3%,故小怡可能投掷的是②号积木.
19.解析 (1),(2)可能发生,也可能不发生,是随机事件.
(3)一定不会发生,是不可能事件.
(4)一定发生,是必然事件.
20.解析 (1)(2)(4)(6)是随机事件.(3)是必然事件.(5)是不可能事件.
21.解析 如果把甲、乙、丙都选择在A献血站献血记为(A,A,A),那么所有的献血选择可以记为(A,A,A),(A,A,B),(A,B,A),(B,A,A),(A,B,B),(B,A,B),(B,B,A),(B,B,B),共8种等可能情况,其中这三人在同一个献血站献血有2种情况,所以这三人在同一个献血站献血的可能性大小为=.
22.解析 (1)P(取出绿球)=1-P(取出黄球)=1-=.
(2)设口袋中的绿球有x个.
根据题意,得=,解得x=18,
经检验,x=18是所列分式方程的解,并且符合实际问题的意义.
答:口袋中的绿球有18个.
23.解析 (1)答案不唯一,如:田、日.
(2)这个游戏不公平.理由:可能出现的结果共有9种,每种结果出现的可能性相等,其中能组成上下结构的汉字的结果有4种:(土,土)“圭”,(口,口)“吕”,(木,口)“杏”,(口,木)“呆”,所以P(小敏获胜)=,P(小慧获胜)=,因为<,所以游戏不公平.
24.解析 (1)x=1 000-412-388=200.
(2)①推荐小明选择B酒店.理由:选择A酒店获得良好用餐体验的可能性大小为=0.8;选择B酒店获得良好用餐体验的可能性大小为=0.81;选择C酒店获得良好用餐体验的可能性大小为=0.78.
∵0.81>0.8>0.78,
∴选择B酒店获得良好用餐体验的可能性最大.
②不一定.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
