13.3.1 等腰三角形
图片预览


文档简介
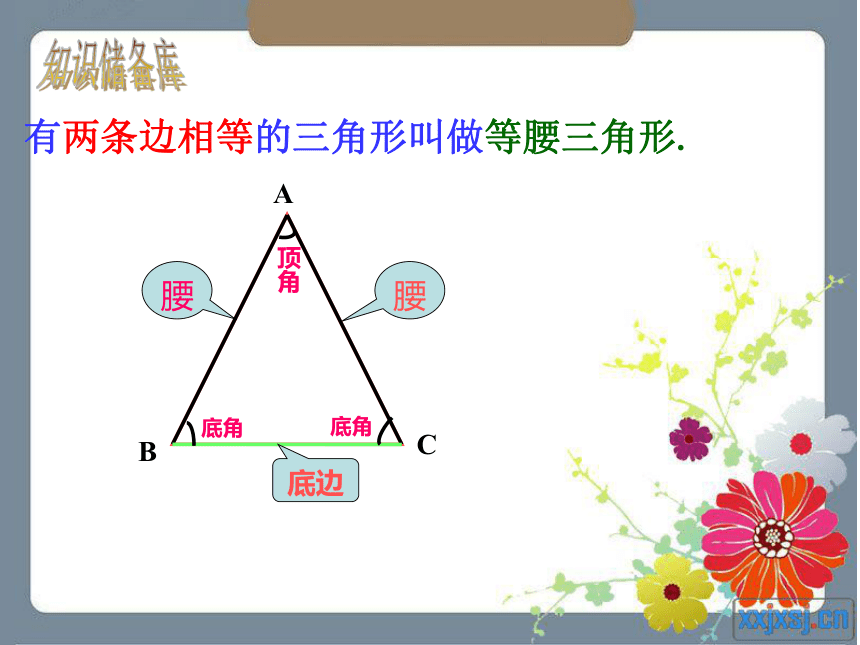
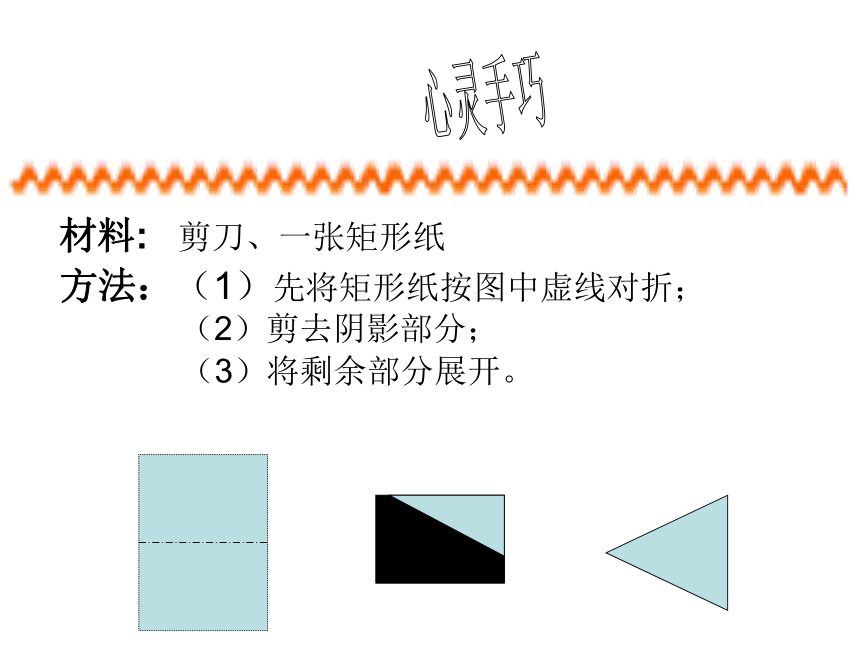
课件28张PPT。13.3.1 等腰三角形科右前旗第七中学 王晓菊有两条边相等的三角形叫做等腰三角形. 底边知识储备库心灵手巧材料: 剪刀、一张矩形纸方法:(1)先将矩形纸按图中虚线对折;
(2)剪去阴影部分; (3)将剩余部分展开。
探索发现1、剪出的是等腰三角形吗? 说说理由。
2、等腰三角形是不是轴对称 图形?它的对成轴在哪?
3、利用轴对称图形的性质,你还可以大胆猜测等腰三角形除了有一组腰长度相等外,还有其他相等的量吗?
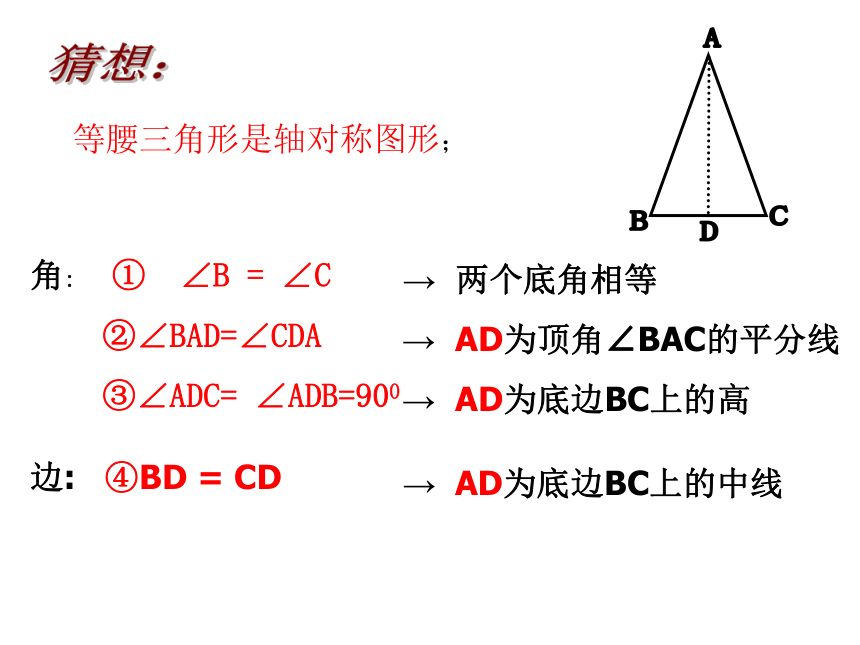
猜想: 角: ① ∠B = ∠C
②∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD → 两个底角相等
→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
等腰三角形是轴对称图形;
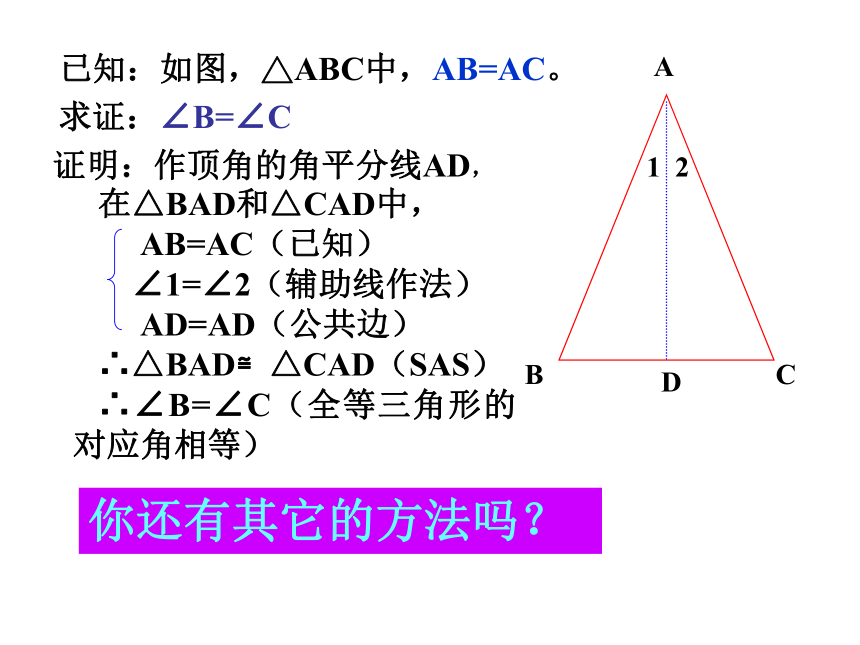
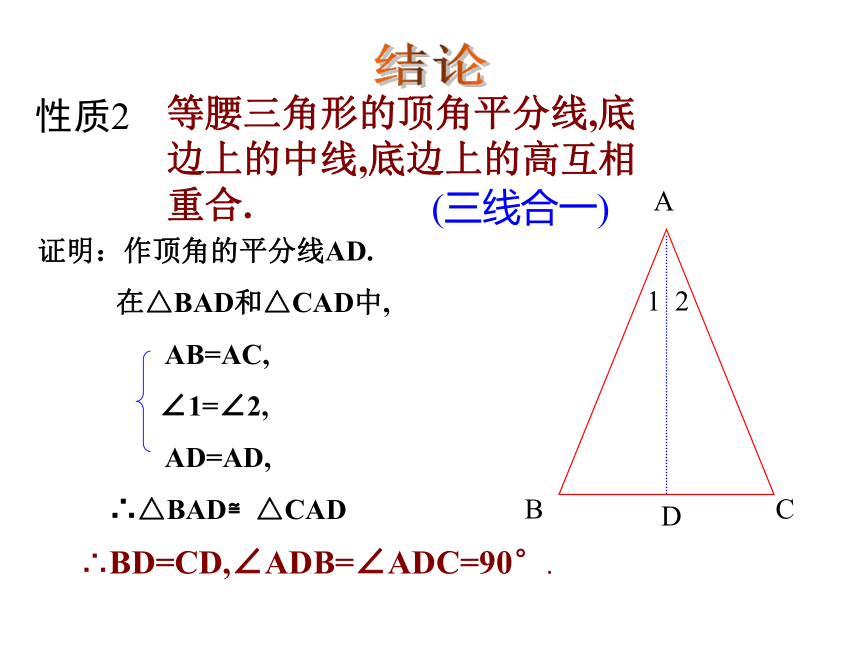
已知:如图,△ABC中,AB=AC。求证:∠B=∠CD12证明:作顶角的角平分线AD,在△BAD和△CAD中,
AB=AC(已知)
∠1=∠2(辅助线作法)
AD=AD(公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
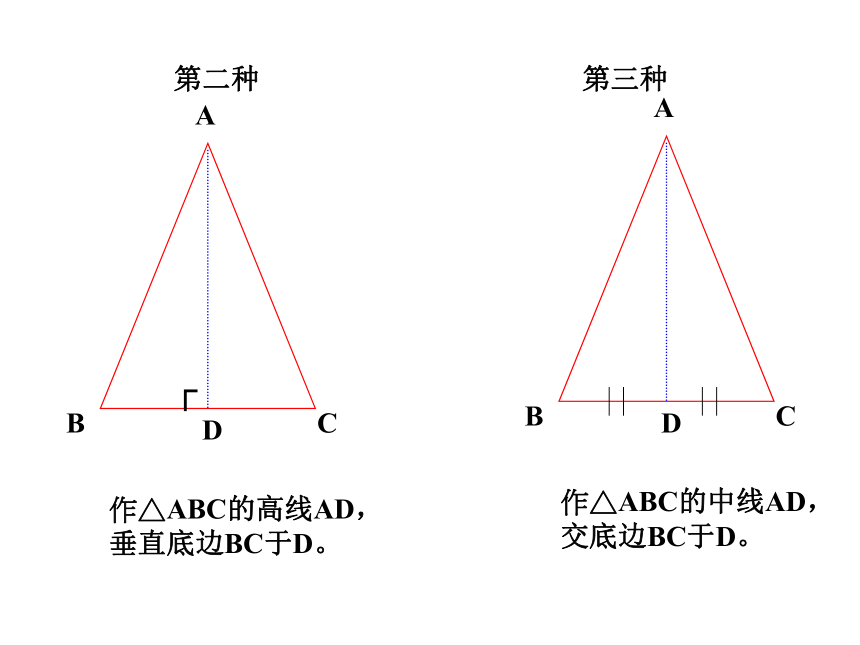
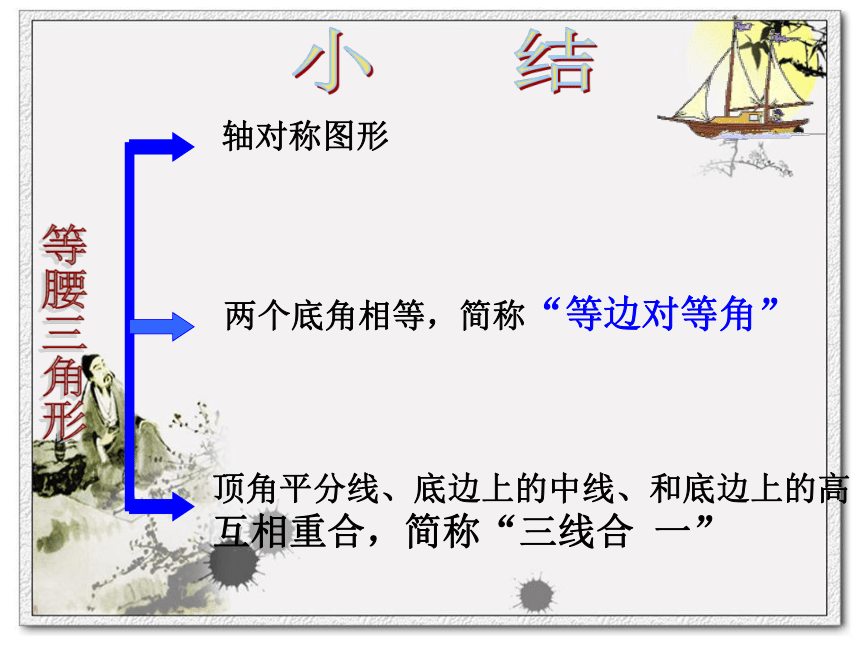
你还有其它的方法吗?第二种第三种DD┌作△ABC的高线AD,垂直底边BC于D。作△ABC的中线AD,交底边BC于D。等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.性质2(三线合一)∴BD=CD,∠ADB=∠ADC=90°.D12结论 轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”等腰三角形小 结1、如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)2、若将条件改为AB=AC ,AD=BD=BC 则有多少个等腰三角形?△ABC(AB=AC)
△ADB(AD=BD)
△BDC (BD=BC)知识的理解 3. 根据等腰三角形的性质2,在△ABC中, 当AB=AC时, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD知识的运用 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= °;72 练习1 填空:
(2)如图,△ABC 中, AB =AC, ∠B =36°, 则∠A
= °; 知识的运用 108练习1 填空:
(3)已知等腰三角形的一个内角为70°,
则它的另外两个内角的度数
分别是 .知识的运用 70°和40°或55 ° 和55°(4)等腰三角形的两边长为4和9,则它的周长是:22 练习2 如图,△ABC 是等腰直角三角形(AB =
AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,
∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的
线段.知识的运用 解:∠B = 45°
∠C = 45°
∠BAD = 45°
∠DAC = 45°BD=AD=DC判断:
(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××知识的运用 知识运用 如图,△ABC 中,BD =BC =AD.
∠CBD= 30°求∠ C、∠A的度数.∠C = 75° ∠A= 37.5°挑战自我 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.χχ2χ2χχ ∠A= 36°趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,
你知道∠CBD的度数吗?
那可以求出∠ MEF的度数吗。这节课你有收获吗?1、“等边对等角”和“三线合一”是证明角、线段相等的新方法,不必再绕到三角形全等来证明
2、等腰三角形辅助线添加方法:作三线之一
布置作业1、预习课本P77-78
2、书面作业:P81第1题,
P82第4 、7题再见(3)等腰三角形两腰上
的中线相等(4)等腰三角形两底角
平分线相等
(5)等腰三角形两腰上的高
相等 利用类似的方法,你还可以得到等腰三角形
中哪些线段相等?DE、DF分别是AB、
AC边上的中线DDE、DF分别是∠ADB、∠ADC
的角平分线
(1)ABDCEAD上任意一点与B、C
的连接线(2)讨论你能用一句话来叙述这个结论吗?等腰三角形的
两个底角相等。等边对等角∵AB=AC
∴∠B=∠C定理的三种表示形式等腰三角形的
两个底角相等。1、文字语言2、符号语言3、图形语言板书D12方法一:角平分线应用格式:∵AB=AC ∠1=∠2
∴BD=DC AD⊥BC1、等腰三角形的顶角的平分线,
既是底边上的中线,又是底边上的高。方法二:作高线D┌3、等腰三角形的底边上的高,
既是底边上的中线,又是顶角平分线。应用格式:
∵AB=AC AD⊥BC ∴BD=DC ∠1=∠2
性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。(通常说成等腰三角形的“三线合一”)性质2可分解成下面三个方面来理解:应用格式:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)2、等腰三角形的底边上中线,既是底边上的高,又是顶角平分线。应用格式:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
ABCD21
(2)剪去阴影部分; (3)将剩余部分展开。
探索发现1、剪出的是等腰三角形吗? 说说理由。
2、等腰三角形是不是轴对称 图形?它的对成轴在哪?
3、利用轴对称图形的性质,你还可以大胆猜测等腰三角形除了有一组腰长度相等外,还有其他相等的量吗?
猜想: 角: ① ∠B = ∠C
②∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD → 两个底角相等
→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
等腰三角形是轴对称图形;
已知:如图,△ABC中,AB=AC。求证:∠B=∠CD12证明:作顶角的角平分线AD,在△BAD和△CAD中,
AB=AC(已知)
∠1=∠2(辅助线作法)
AD=AD(公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
你还有其它的方法吗?第二种第三种DD┌作△ABC的高线AD,垂直底边BC于D。作△ABC的中线AD,交底边BC于D。等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.性质2(三线合一)∴BD=CD,∠ADB=∠ADC=90°.D12结论 轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”等腰三角形小 结1、如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)2、若将条件改为AB=AC ,AD=BD=BC 则有多少个等腰三角形?△ABC(AB=AC)
△ADB(AD=BD)
△BDC (BD=BC)知识的理解 3. 根据等腰三角形的性质2,在△ABC中, 当AB=AC时, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD知识的运用 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= °;72 练习1 填空:
(2)如图,△ABC 中, AB =AC, ∠B =36°, 则∠A
= °; 知识的运用 108练习1 填空:
(3)已知等腰三角形的一个内角为70°,
则它的另外两个内角的度数
分别是 .知识的运用 70°和40°或55 ° 和55°(4)等腰三角形的两边长为4和9,则它的周长是:22 练习2 如图,△ABC 是等腰直角三角形(AB =
AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,
∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的
线段.知识的运用 解:∠B = 45°
∠C = 45°
∠BAD = 45°
∠DAC = 45°BD=AD=DC判断:
(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××知识的运用 知识运用 如图,△ABC 中,BD =BC =AD.
∠CBD= 30°求∠ C、∠A的度数.∠C = 75° ∠A= 37.5°挑战自我 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.χχ2χ2χχ ∠A= 36°趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,
你知道∠CBD的度数吗?
那可以求出∠ MEF的度数吗。这节课你有收获吗?1、“等边对等角”和“三线合一”是证明角、线段相等的新方法,不必再绕到三角形全等来证明
2、等腰三角形辅助线添加方法:作三线之一
布置作业1、预习课本P77-78
2、书面作业:P81第1题,
P82第4 、7题再见(3)等腰三角形两腰上
的中线相等(4)等腰三角形两底角
平分线相等
(5)等腰三角形两腰上的高
相等 利用类似的方法,你还可以得到等腰三角形
中哪些线段相等?DE、DF分别是AB、
AC边上的中线DDE、DF分别是∠ADB、∠ADC
的角平分线
(1)ABDCEAD上任意一点与B、C
的连接线(2)讨论你能用一句话来叙述这个结论吗?等腰三角形的
两个底角相等。等边对等角∵AB=AC
∴∠B=∠C定理的三种表示形式等腰三角形的
两个底角相等。1、文字语言2、符号语言3、图形语言板书D12方法一:角平分线应用格式:∵AB=AC ∠1=∠2
∴BD=DC AD⊥BC1、等腰三角形的顶角的平分线,
既是底边上的中线,又是底边上的高。方法二:作高线D┌3、等腰三角形的底边上的高,
既是底边上的中线,又是顶角平分线。应用格式:
∵AB=AC AD⊥BC ∴BD=DC ∠1=∠2
性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。(通常说成等腰三角形的“三线合一”)性质2可分解成下面三个方面来理解:应用格式:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)2、等腰三角形的底边上中线,既是底边上的高,又是顶角平分线。应用格式:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
ABCD21
