梯形的中位线
图片预览



文档简介
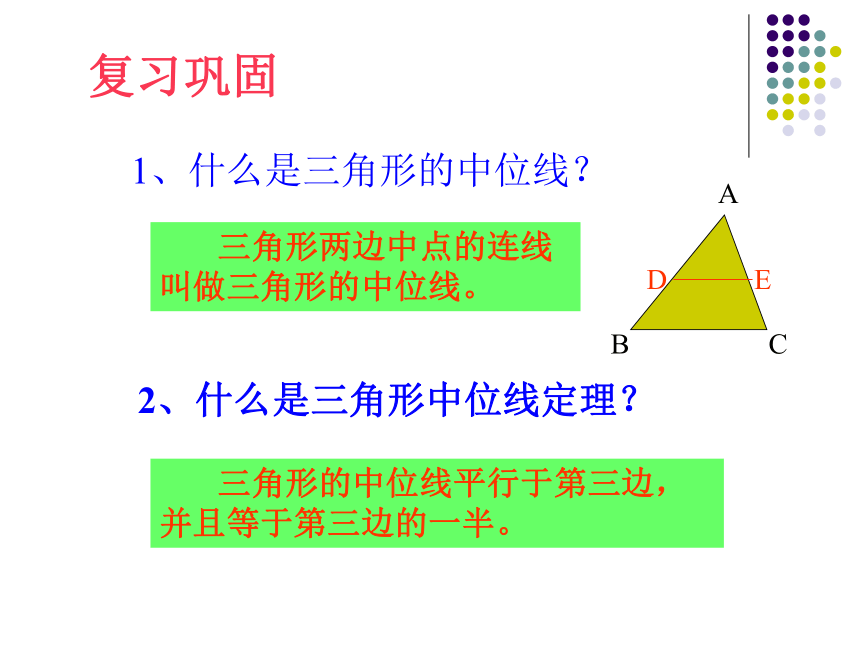
课件33张PPT。2.梯形的中位线 24.4中位线义务教育课程标准实验教科书华东师大版 三角形的中位线平行于第三边,并且等于第三边的一半。 三角形两边中点的连线叫做三角形的中位线。复习巩固怎样将一张梯形硬纸片剪成两部分,使分成的两部分能拼成一个三角形?操作:
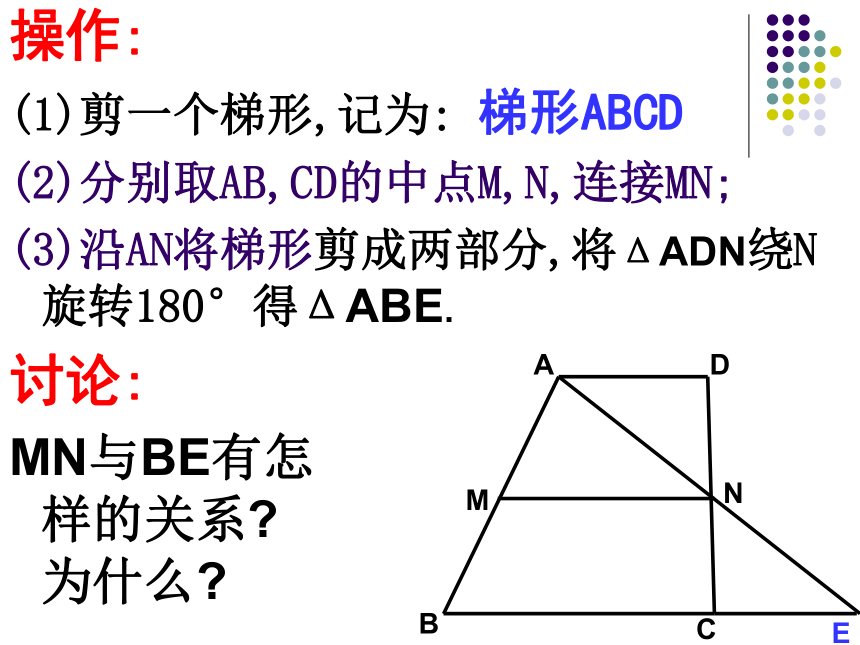
(1)剪一个梯形,记为: 梯形ABCD
(2)分别取AB,CD的中点M,N,连接MN;
(3)沿AN将梯形剪成两部分,将ΔADN绕N旋转180°得ΔABE.
讨论:
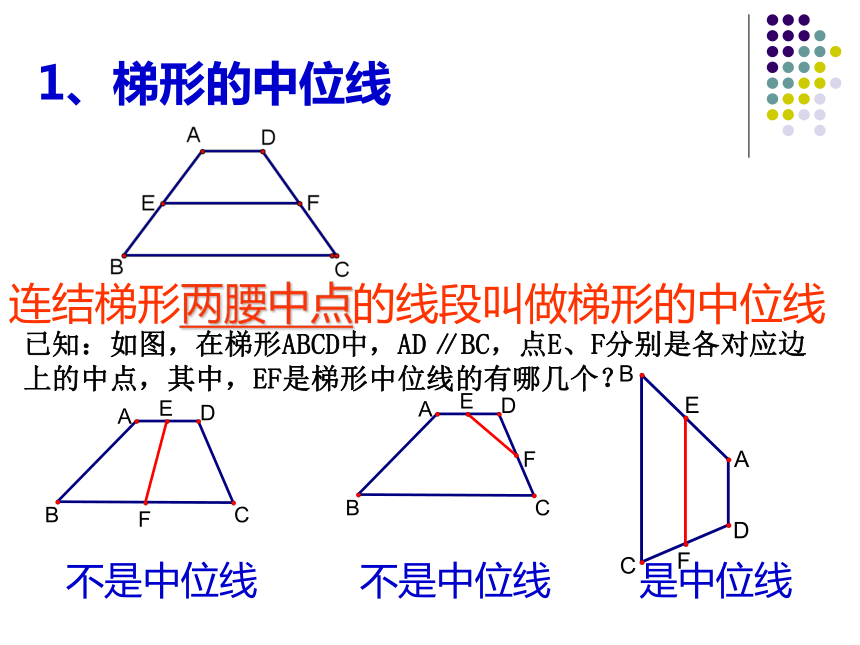
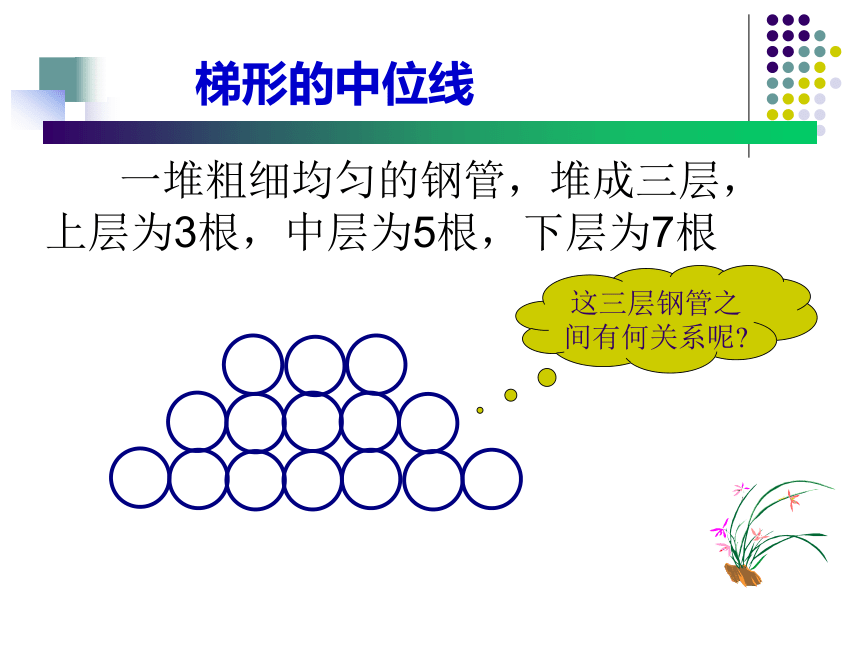
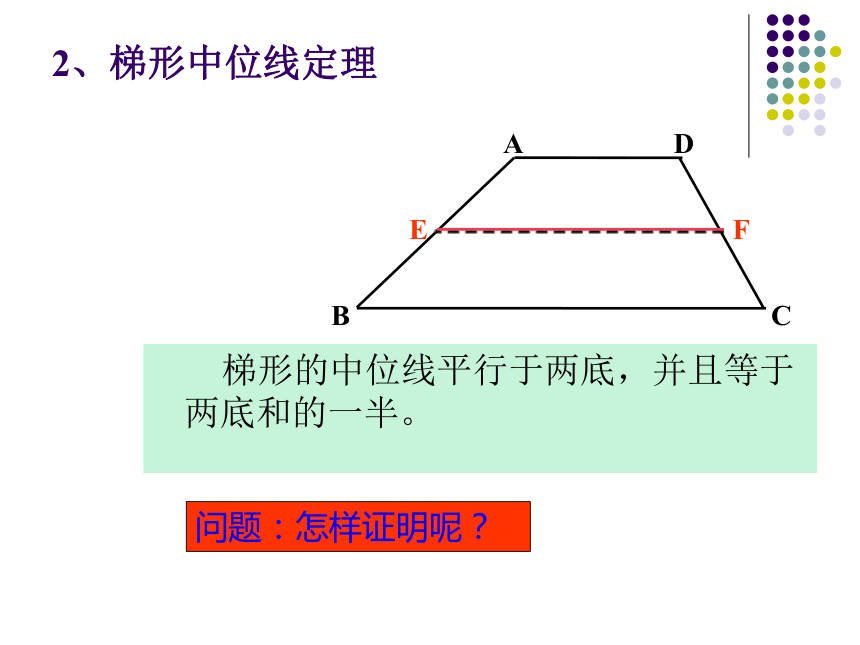
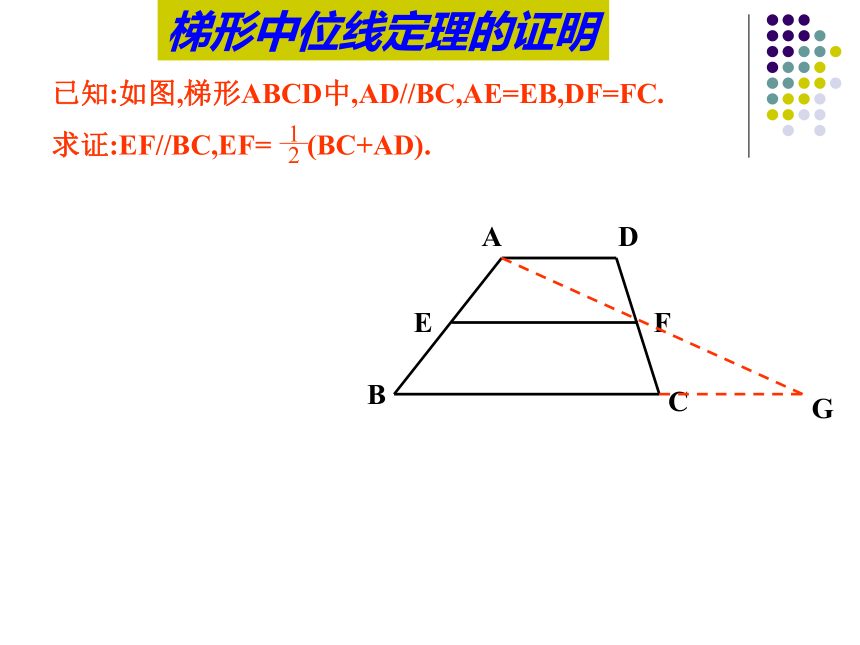
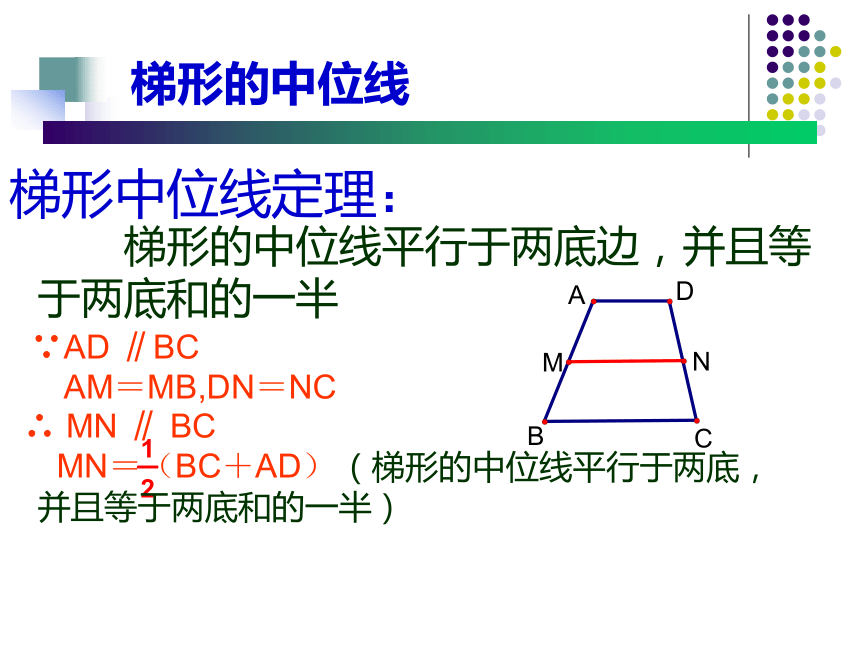
MN与BE有怎 样的关系? 为什么?MN1、梯形的中位线连结梯形两腰中点的线段叫做梯形的中位线已知:如图,在梯形ABCD中,AD ∥BC,点E、F分别是各对应边上的中点,其中,EF是梯形中位线的有哪几个?不是中位线不是中位线是中位线梯形的中位线 一堆粗细均匀的钢管,堆成三层,上层为3根,中层为5根,下层为7根这三层钢管之间有何关系呢?2、梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半。问题:怎样证明呢?梯形中位线定理的证明梯形的中位线 梯形的中位线平行于两底边,并且等于两底和的一半梯形中位线定理:∵AD ∥BC
AM=MB,DN=NC∴ MN ∥ BC
MN=(BC+AD) (梯形的中位线平行于两底,
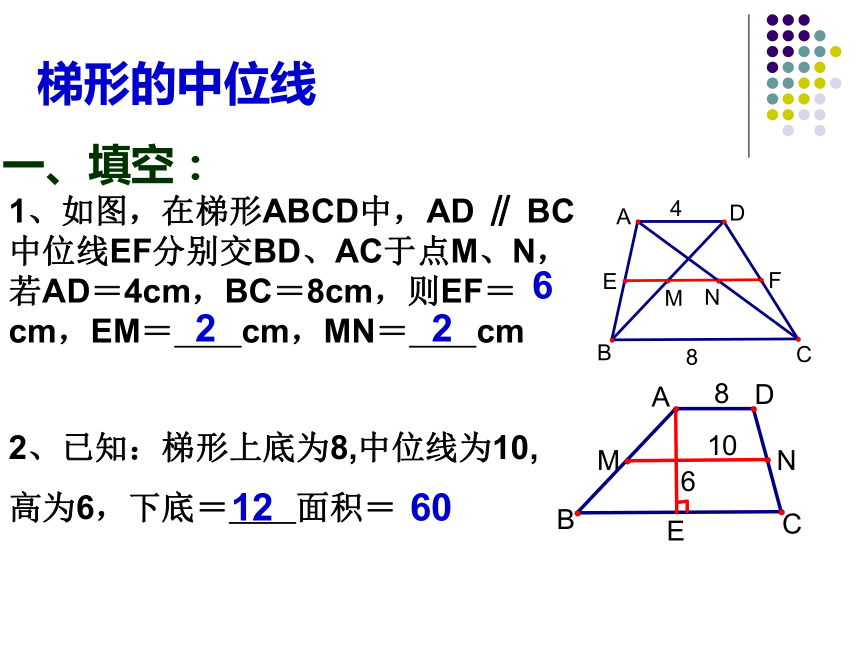
并且等于两底和的一半)梯形的中位线2、已知:梯形上底为8,中位线为10,
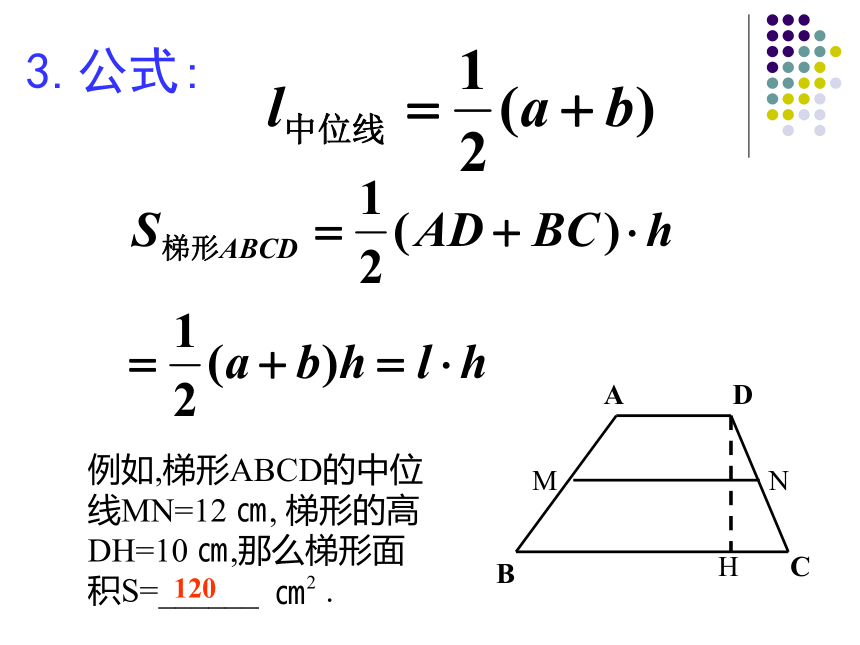
高为6,下底= 面积= 一、填空:12601、如图,在梯形ABCD中,AD ∥ BC中位线EF分别交BD、AC于点M、N,若AD=4cm,BC=8cm,则EF= cm,EM= cm,MN= cm6221203.公式:1、一个梯形的上底长4 cm,下底长6 cm,则其中位线长为 cm;
2、一个梯形的上底长10 cm,中位线长16 cm,则其下底长为 cm;
3、已知梯形的中位线长为6 cm,高为8 cm,则该梯形的面积为________ cm2 ;
4、已知等腰梯形的周长为80 cm,中位线与腰长相等,则它的中位线长 cm;小试牛刀5224820 正确答案:9cm;12cm.答:不能.如果和一条底边长相等,那么和另一条底边长也相等,这时四边形的对边平行且相等,这是平行四边形而不是梯形.5.梯形的上底长8cm,下底长10cm,则中位线长_______;
梯形的上底长8cm,中位线长10cm,则下底长_______.
6.梯形的中位线长能不能与它的一条底边长相等?为什么?
小试牛刀7. 如图所示的梯形梯子,AA'∥EE',AB=BC=CD=DE,A' B'=B' C'=C' D'=D' E', AA'=0.5 m, EE'=0.8 m.求BB'、CC'、DD'的长.小试牛刀作 高平 移 腰1.以上图中相等的线段,相等的角2.平移腰可将梯形的两腰、两底角放置在一个三角形.平 移 对 角 线1、当AC⊥BD时,ΔBED是什么三角形?2、当AC =BD时,ΔBED又是什么三角形?3、哪个命题的证明应用了此法?对角线相等的梯形是等腰梯形4 、 ΔBED与梯形ABCD的面积关系如何?补 三 角 形1、 若梯形ABCD是等腰梯形时,ΔOBC是什么三角形?2、梯形满足什么条件时, ΔOBC是直角三角形?
其他方法构造旋转变换梯形ABCD面积与哪个图形面积相等?作 高例1、在梯形ABCD中,DC∥AB,腰AD=BC,CE⊥AB,BE=1cm,中位线长为2.5cm,求底AB和DC的长ABCDEF练习:如图,在等腰梯形ABCD中,AD∥BC,
BC-AD=4cm,GH为梯形的中位线,
GH=6cm,AB=CD=4cm,求该梯形的面积.ABDCEF解:过A、D分别作梯形ABCD的高AE、DF.∴AE=BF,∠AEB=∠DFC=90°在Rt△ABE与Rt△DCF中∴ Rt△ABE≌Rt△DCF (HL)GHEF∴ BE=CF∴ BE=CF= (BC-AD)=2 ∴在Rt△ABE中,
AE= =2∴ 梯形ABCD的面积= GH×AE =6× =12 cm2 GH构造三角形中位线例2、如图,梯形ABCD中,M,N分别是对角线BD,AC的中点 求证:MN∥BC,MN=(BC-AD)/2其他方法构造旋转变换梯形ABCD面积与哪个图形面积相等?例3:如图,在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD的中点.求证:AE⊥BE.
DB平 移 对 角 线例4、如图:在梯形ABCD中,AD∥BC,对角线AC⊥BD,
EF为梯形的中位线,∠DBC=30°,求证:EF=AC。BDAEFCOG对角线垂直时通常平移对角线 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线长是 …( )
A.10 B. C. D.12 E练一练 如图,等腰梯形ABCD的两条对角线互相垂直, EF为中位线, DH是梯形的高. 求证:EF=DH.略证:
过点D作AC的平行线,交BC的延长线于G.则△BDC为等腰直角三角形,四边形ACGD为平行四边形,所以
DH= BG= 1/2 (BC+CG)= 1/2 (BC+AD).
又EF= 1/2 (BC+AD),故EF=DH.思维拓展分析:过点D作AC的平行线,交BC的延长线于G.小结1.梯形的中位线概念.
2. 梯形中位线定理:
梯形的中位线平行于两底,并且等于两底和的一半
3.梯形的面积公式:
(1)剪一个梯形,记为: 梯形ABCD
(2)分别取AB,CD的中点M,N,连接MN;
(3)沿AN将梯形剪成两部分,将ΔADN绕N旋转180°得ΔABE.
讨论:
MN与BE有怎 样的关系? 为什么?MN1、梯形的中位线连结梯形两腰中点的线段叫做梯形的中位线已知:如图,在梯形ABCD中,AD ∥BC,点E、F分别是各对应边上的中点,其中,EF是梯形中位线的有哪几个?不是中位线不是中位线是中位线梯形的中位线 一堆粗细均匀的钢管,堆成三层,上层为3根,中层为5根,下层为7根这三层钢管之间有何关系呢?2、梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半。问题:怎样证明呢?梯形中位线定理的证明梯形的中位线 梯形的中位线平行于两底边,并且等于两底和的一半梯形中位线定理:∵AD ∥BC
AM=MB,DN=NC∴ MN ∥ BC
MN=(BC+AD) (梯形的中位线平行于两底,
并且等于两底和的一半)梯形的中位线2、已知:梯形上底为8,中位线为10,
高为6,下底= 面积= 一、填空:12601、如图,在梯形ABCD中,AD ∥ BC中位线EF分别交BD、AC于点M、N,若AD=4cm,BC=8cm,则EF= cm,EM= cm,MN= cm6221203.公式:1、一个梯形的上底长4 cm,下底长6 cm,则其中位线长为 cm;
2、一个梯形的上底长10 cm,中位线长16 cm,则其下底长为 cm;
3、已知梯形的中位线长为6 cm,高为8 cm,则该梯形的面积为________ cm2 ;
4、已知等腰梯形的周长为80 cm,中位线与腰长相等,则它的中位线长 cm;小试牛刀5224820 正确答案:9cm;12cm.答:不能.如果和一条底边长相等,那么和另一条底边长也相等,这时四边形的对边平行且相等,这是平行四边形而不是梯形.5.梯形的上底长8cm,下底长10cm,则中位线长_______;
梯形的上底长8cm,中位线长10cm,则下底长_______.
6.梯形的中位线长能不能与它的一条底边长相等?为什么?
小试牛刀7. 如图所示的梯形梯子,AA'∥EE',AB=BC=CD=DE,A' B'=B' C'=C' D'=D' E', AA'=0.5 m, EE'=0.8 m.求BB'、CC'、DD'的长.小试牛刀作 高平 移 腰1.以上图中相等的线段,相等的角2.平移腰可将梯形的两腰、两底角放置在一个三角形.平 移 对 角 线1、当AC⊥BD时,ΔBED是什么三角形?2、当AC =BD时,ΔBED又是什么三角形?3、哪个命题的证明应用了此法?对角线相等的梯形是等腰梯形4 、 ΔBED与梯形ABCD的面积关系如何?补 三 角 形1、 若梯形ABCD是等腰梯形时,ΔOBC是什么三角形?2、梯形满足什么条件时, ΔOBC是直角三角形?
其他方法构造旋转变换梯形ABCD面积与哪个图形面积相等?作 高例1、在梯形ABCD中,DC∥AB,腰AD=BC,CE⊥AB,BE=1cm,中位线长为2.5cm,求底AB和DC的长ABCDEF练习:如图,在等腰梯形ABCD中,AD∥BC,
BC-AD=4cm,GH为梯形的中位线,
GH=6cm,AB=CD=4cm,求该梯形的面积.ABDCEF解:过A、D分别作梯形ABCD的高AE、DF.∴AE=BF,∠AEB=∠DFC=90°在Rt△ABE与Rt△DCF中∴ Rt△ABE≌Rt△DCF (HL)GHEF∴ BE=CF∴ BE=CF= (BC-AD)=2 ∴在Rt△ABE中,
AE= =2∴ 梯形ABCD的面积= GH×AE =6× =12 cm2 GH构造三角形中位线例2、如图,梯形ABCD中,M,N分别是对角线BD,AC的中点 求证:MN∥BC,MN=(BC-AD)/2其他方法构造旋转变换梯形ABCD面积与哪个图形面积相等?例3:如图,在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD的中点.求证:AE⊥BE.
DB平 移 对 角 线例4、如图:在梯形ABCD中,AD∥BC,对角线AC⊥BD,
EF为梯形的中位线,∠DBC=30°,求证:EF=AC。BDAEFCOG对角线垂直时通常平移对角线 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线长是 …( )
A.10 B. C. D.12 E练一练 如图,等腰梯形ABCD的两条对角线互相垂直, EF为中位线, DH是梯形的高. 求证:EF=DH.略证:
过点D作AC的平行线,交BC的延长线于G.则△BDC为等腰直角三角形,四边形ACGD为平行四边形,所以
DH= BG= 1/2 (BC+CG)= 1/2 (BC+AD).
又EF= 1/2 (BC+AD),故EF=DH.思维拓展分析:过点D作AC的平行线,交BC的延长线于G.小结1.梯形的中位线概念.
2. 梯形中位线定理:
梯形的中位线平行于两底,并且等于两底和的一半
3.梯形的面积公式:
