人教版九年级上册22.1.4 二次函数y=ax?+bx+c的图象和性质(第1课时)课件(共15张PPT)
文档属性
| 名称 | 人教版九年级上册22.1.4 二次函数y=ax?+bx+c的图象和性质(第1课时)课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 14:11:28 | ||
图片预览





文档简介
(共16张PPT)
第 二十二 章 二次函数
数学 九年级 上册 R
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第1课时 二次函数y=ax2+bx+c的图象和性质
回顾:二次函数y=a(x-h)2+k的性质
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当xy随着x的增大而减小。
当x>h时,
y随着x的增大而增大。
当xy随着x的增大而增大。
当x>h时,
y随着x的增大而减小。
x=h时,y最小值=k
x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过上下和左右平移得到.
我们已经知道二次函数y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论二次函数 图象和性质
分析:这种函数形式并不是我们所熟悉的二次函数,所以考虑将其变形
配方可得:
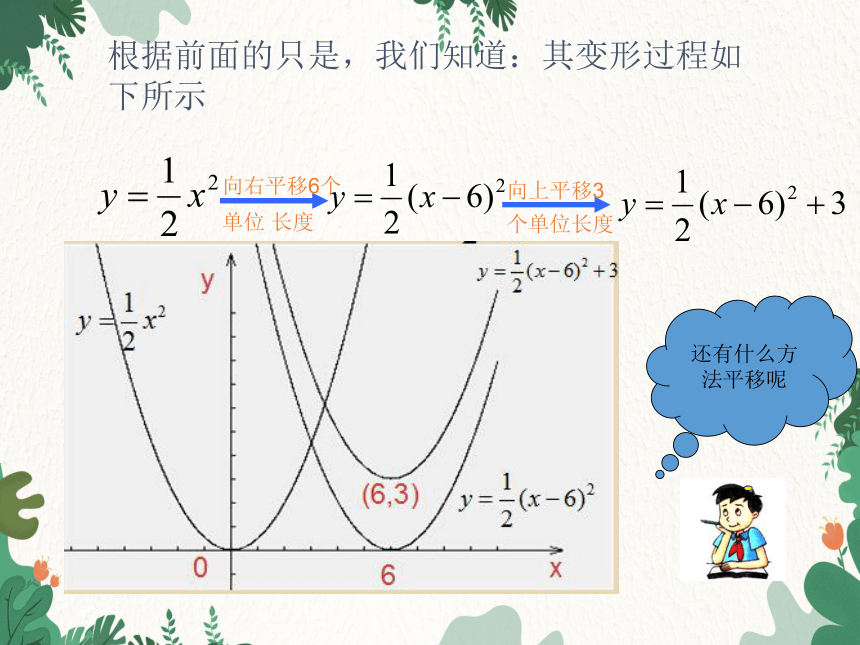
根据前面的只是,我们知道:其变形过程如下所示
向右平移6个单位 长度
向上平移3个单位长度
还有什么方
法平移呢
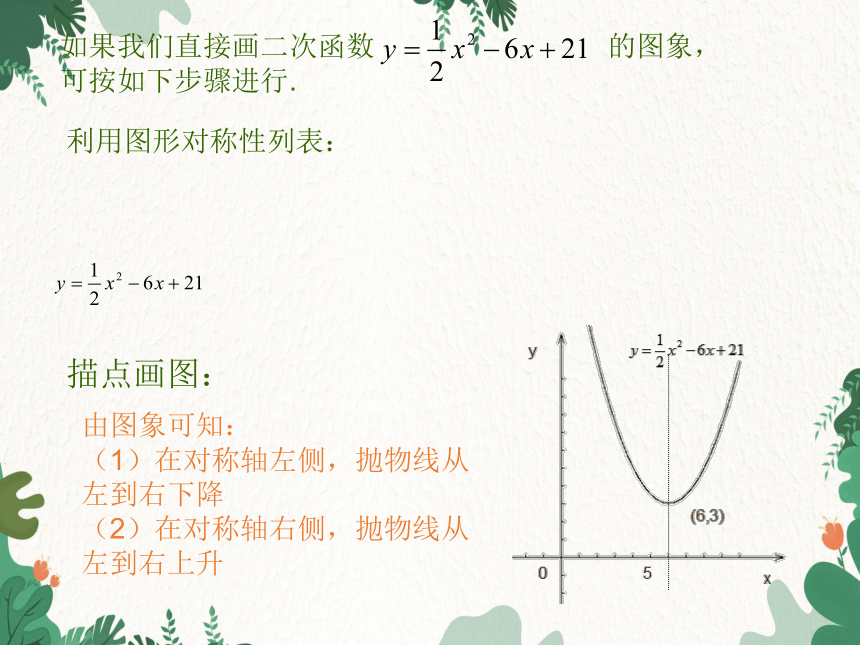
如果我们直接画二次函数 的图象,可按如下步骤进行.
利用图形对称性列表:
描点画图:
由图象可知:
(1)在对称轴左侧,抛物线从左到右下降
(2)在对称轴右侧,抛物线从左到右上升
你能用上面的方法讨论二次函数 的图象和性质吗?
试一试
一般的,二次函数y=ax2+bx+c可以通过配方化成y=a(x-h)2+k的形式,即
因此,其对称轴是:
顶点是:
从二次函数y=ax2+bx+c的图象可以看出:
(1):如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大.
(2):如果a<0,当 时,y随x的增大而
减小,当 时,y随x的增大而增大.
你知道吗
用配方法
分析思考
试一试
∴开口方向:由a决定;
要记住公式哦!
试一试
我来模仿
试一试
1.抛物线y=x2-4x+3与y轴的交点坐标是 ,
与x轴的交点坐标是 。
(0,3)
(1,0)或(3,0)
抛物线与y轴的交点有什么特征?
抛物线与x轴的交点有什么特征?
当堂训练
写出下列抛物线的开口方向、对称轴和顶点:
当堂训练
第 二十二 章 二次函数
数学 九年级 上册 R
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第1课时 二次函数y=ax2+bx+c的图象和性质
回顾:二次函数y=a(x-h)2+k的性质
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当x
当x>h时,
y随着x的增大而增大。
当x
当x>h时,
y随着x的增大而减小。
x=h时,y最小值=k
x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通过上下和左右平移得到.
我们已经知道二次函数y=a(x-h)2+k的图象和性质,能否利用这些知识来讨论二次函数 图象和性质
分析:这种函数形式并不是我们所熟悉的二次函数,所以考虑将其变形
配方可得:
根据前面的只是,我们知道:其变形过程如下所示
向右平移6个单位 长度
向上平移3个单位长度
还有什么方
法平移呢
如果我们直接画二次函数 的图象,可按如下步骤进行.
利用图形对称性列表:
描点画图:
由图象可知:
(1)在对称轴左侧,抛物线从左到右下降
(2)在对称轴右侧,抛物线从左到右上升
你能用上面的方法讨论二次函数 的图象和性质吗?
试一试
一般的,二次函数y=ax2+bx+c可以通过配方化成y=a(x-h)2+k的形式,即
因此,其对称轴是:
顶点是:
从二次函数y=ax2+bx+c的图象可以看出:
(1):如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大.
(2):如果a<0,当 时,y随x的增大而
减小,当 时,y随x的增大而增大.
你知道吗
用配方法
分析思考
试一试
∴开口方向:由a决定;
要记住公式哦!
试一试
我来模仿
试一试
1.抛物线y=x2-4x+3与y轴的交点坐标是 ,
与x轴的交点坐标是 。
(0,3)
(1,0)或(3,0)
抛物线与y轴的交点有什么特征?
抛物线与x轴的交点有什么特征?
当堂训练
写出下列抛物线的开口方向、对称轴和顶点:
当堂训练
同课章节目录
