12.2 三角形全等的判定(第4课时)课件(共35张PPT)
文档属性
| 名称 | 12.2 三角形全等的判定(第4课时)课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 885.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 16:28:56 | ||
图片预览








文档简介
(共35张PPT)
12.2 三角形全等的判定
(第4课时)
人教版 数学 八年级 上册
舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.
(1) 你能帮他想个办法吗?
根据SAS可测量其余两边与这两边的夹角.
根据ASA,AAS可测量对应一边和一锐角.
导入新知
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等。于是,他就肯定“两个直角三角形是全等的”.
你相信这个结论吗?
(2)如果他只带一个卷尺,能完成这个任务吗
让我们来探究一下吧!
斜边和一条直角边对应相等→两个直角三角形全等.
导入新知
2. 能运用三角形全等的判定方法判断两个直角三角形全等.
1. 探究直角三角形全等的判定方法.
素养目标
SSS
SAS
ASA
AAS
旧知回顾 我们学过的判定三角形全等的方法.
探究新知
知识点
三角形全等的判定——“HL”定理
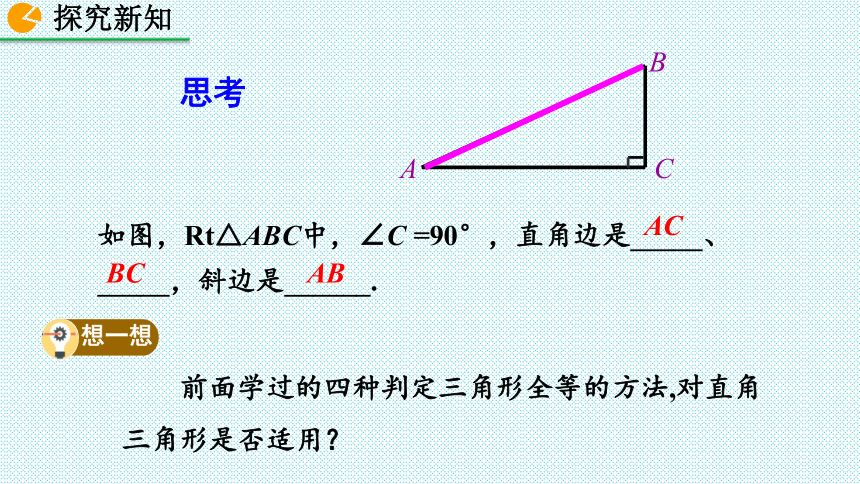
如图,Rt△ABC中,∠C =90°,直角边是_____、_____,斜边是______.
C
B
A
AC
BC
AB
思考
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
探究新知
想一想
A
B
C
B′
C′
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
3.两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
探究新知
问题
A′
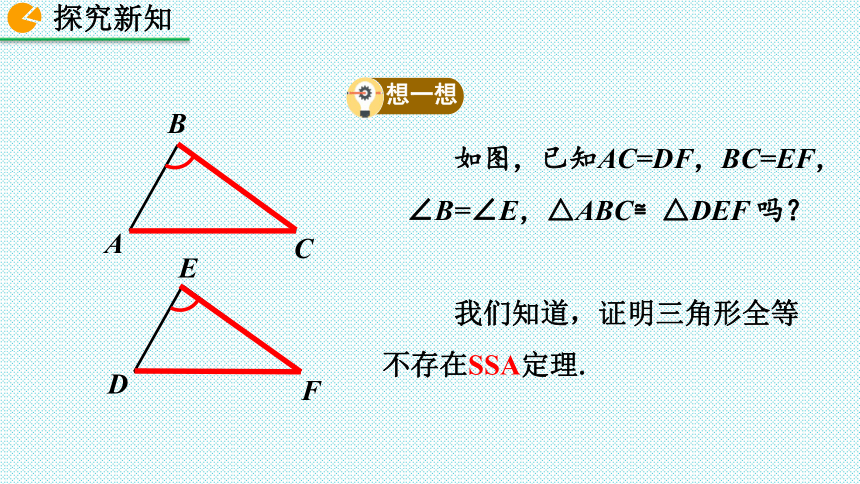
如图,已知AC=DF,BC=EF,∠B=∠E,△ABC≌△DEF 吗?
我们知道,证明三角形全等
不存在SSA定理.
A
B
C
D
E
F
探究新知
想一想
如果这两个三角形都是直
角三角形,即∠B=∠E=90°,
且AC=DF,BC=EF,现在能
判定△ABC≌△DEF吗?
A
B
C
D
E
F
探究新知
想一想
任意画出一个Rt△ABC ,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 ° , B′C′=BC , A ′B ′=AB ,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
探究新知
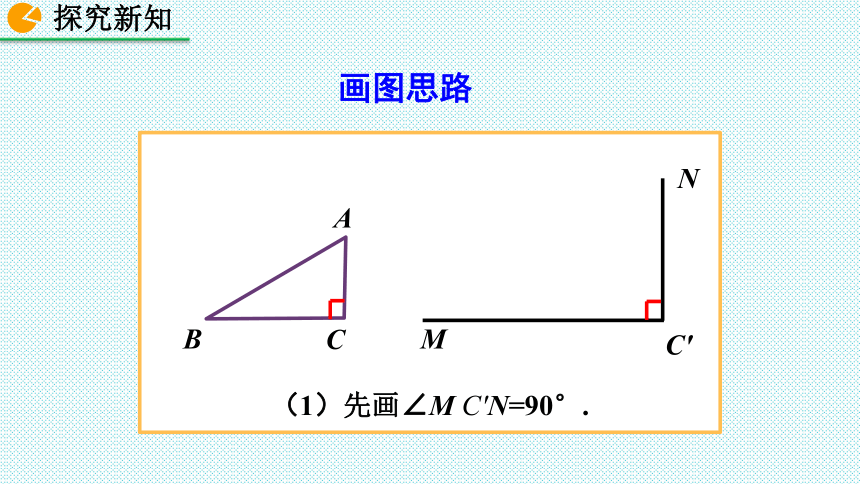
画图思路
(1)先画∠M C′ N=90°.
A
B
C
M
C′
N
探究新知
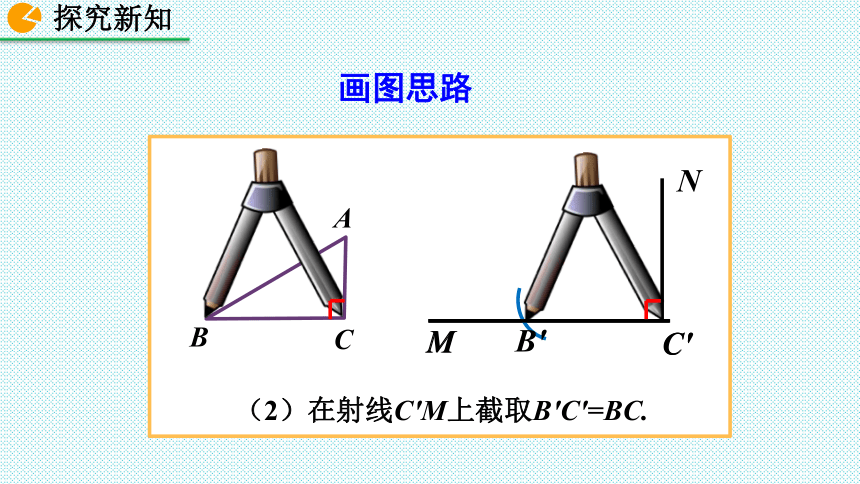
(2)在射线C′M上截取B′C′=BC.
M
C′
A
B
C
N
B′
M
C′
探究新知
画图思路
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′.
M
C′
A
B
C
N
B′
A′
探究新知
画图思路
(4)连接A′B′.
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
探究新知
画图思路
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
探究新知
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等; ( )
(2)一个锐角和这个角的邻边对应相等; ( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
HL
AAS或ASA
SAS
AAS
AAS
判一判
探究新知
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD.
求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D 都是直角.
AB=BA,
AC=BD .
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
探究新知
利用“HL”定理判定直角三角形全等
素养考点 1
如图,∠ACB =∠ADB=90 ° ,要证明△ABC≌△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
探究新知
变式 题 1
如图,AC,BD相交于点P , AC⊥BC,BD⊥AD,垂足分别为C,D , AD=BC.求证:AC=BD.
HL
AC=BD
Rt△ABD≌Rt△BAC
探究新知
变 式 题 2
如图:AB⊥AD,CD⊥BC , AB=CD ,判断AD和BC的位置关系.
HL
∠ADB=∠CBD
Rt△ABD≌Rt△CDB
AD∥BC
探究新知
变 式 题 3
如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.
证明:在Rt△ABE和Rt△CBF中,∠ABE=∠CBF=90°,
∵AB=CB,AE=CF ,
∴Rt△ABE≌Rt△CBF(HL).
巩固练习
例2 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF. 即BC=BE.
探究新知
探究新知
方法点拨
证明线段相等可通过证明三角形全等解决,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
如图,已知AE⊥BC,DF⊥BC,E,F是垂足,AE=DF,AB=DC,求证:AC=DB.
证明:AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°.
在Rt△ABE和Rt△DCF中, AE=DF , AB=DC,
∴Rt△ABE≌Rt△DCF(HL),
∴∠ABC=∠DCB.
在△ABC和△DCB中, AB=DC,∠ABC=∠DCB, BC =CB,
∴△ABC≌△DCB(SAS),
∴AC=DB .
巩固练习
例3 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF(全等三角形对应角相等).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
探究新知
利用直角三角形全等解决实际问题
素养考点 2
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
所以Rt△ABD≌Rt△ACD.(HL)
所以BD=CD.
解:BD=CD.
因为∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
AB=AC,
AD=AD,
巩固练习
1.如图,∠A=∠D=90°,AC=DB,AC,DB相交于点O.
求证:OB=OC.
证明:在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
连接中考
证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,
∴∠AED=∠CFD=90°,
∵D为AC的中点,∴AD=DC,
在Rt△ADE和Rt△CDF中,,
∴Rt△ADE≌Rt△CDF,
∴∠A=∠C,∴BA=BC,∵AB=AC,
∴AB=BC=AC,
∴△ABC是等边三角形.
2.已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.
连接中考
D
1. 判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
课堂检测
基础巩固题
2. 如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点
E ,AD、CE交于点H,已知EH=EB=3,AE=4,
则 CH的长为( )
A.1 B.2 C.3 D.4
3.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等”),根据 (用简写法).
全等
HL
课堂检测
A
4. 如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明:∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴ Rt△EBC≌Rt△DCB (HL).
课堂检测
如图,AB=CD, BF⊥AC,DE⊥AC, AE=CF.求证:BF=DE.
证明: ∵ BF⊥AC,DE⊥AC,
∴∠BFA=∠DEC=90 °.
∵AE=CF,
∴AE+EF=CF+EF.即AF=CE.
在Rt△ABF和Rt△CDE中,
AB=CD,
AF=CE.
∴ Rt△ABF≌Rt△CDE(HL).
A
F
C
E
D
B
∴BF=DE.
能力提升题
课堂检测
如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P,Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
拓广探索题
课堂检测
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm,
∴当AP=5cm或10cm时,△ABC才能和△APQ全等.
课堂检测
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm;
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
课堂小结
12.2 三角形全等的判定
(第4课时)
人教版 数学 八年级 上册
舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.
(1) 你能帮他想个办法吗?
根据SAS可测量其余两边与这两边的夹角.
根据ASA,AAS可测量对应一边和一锐角.
导入新知
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等。于是,他就肯定“两个直角三角形是全等的”.
你相信这个结论吗?
(2)如果他只带一个卷尺,能完成这个任务吗
让我们来探究一下吧!
斜边和一条直角边对应相等→两个直角三角形全等.
导入新知
2. 能运用三角形全等的判定方法判断两个直角三角形全等.
1. 探究直角三角形全等的判定方法.
素养目标
SSS
SAS
ASA
AAS
旧知回顾 我们学过的判定三角形全等的方法.
探究新知
知识点
三角形全等的判定——“HL”定理
如图,Rt△ABC中,∠C =90°,直角边是_____、_____,斜边是______.
C
B
A
AC
BC
AB
思考
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
探究新知
想一想
A
B
C
B′
C′
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
3.两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
探究新知
问题
A′
如图,已知AC=DF,BC=EF,∠B=∠E,△ABC≌△DEF 吗?
我们知道,证明三角形全等
不存在SSA定理.
A
B
C
D
E
F
探究新知
想一想
如果这两个三角形都是直
角三角形,即∠B=∠E=90°,
且AC=DF,BC=EF,现在能
判定△ABC≌△DEF吗?
A
B
C
D
E
F
探究新知
想一想
任意画出一个Rt△ABC ,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 ° , B′C′=BC , A ′B ′=AB ,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
探究新知
画图思路
(1)先画∠M C′ N=90°.
A
B
C
M
C′
N
探究新知
(2)在射线C′M上截取B′C′=BC.
M
C′
A
B
C
N
B′
M
C′
探究新知
画图思路
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′.
M
C′
A
B
C
N
B′
A′
探究新知
画图思路
(4)连接A′B′.
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
探究新知
画图思路
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
探究新知
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等; ( )
(2)一个锐角和这个角的邻边对应相等; ( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
HL
AAS或ASA
SAS
AAS
AAS
判一判
探究新知
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD.
求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D 都是直角.
AB=BA,
AC=BD .
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
探究新知
利用“HL”定理判定直角三角形全等
素养考点 1
如图,∠ACB =∠ADB=90 ° ,要证明△ABC≌△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
探究新知
变式 题 1
如图,AC,BD相交于点P , AC⊥BC,BD⊥AD,垂足分别为C,D , AD=BC.求证:AC=BD.
HL
AC=BD
Rt△ABD≌Rt△BAC
探究新知
变 式 题 2
如图:AB⊥AD,CD⊥BC , AB=CD ,判断AD和BC的位置关系.
HL
∠ADB=∠CBD
Rt△ABD≌Rt△CDB
AD∥BC
探究新知
变 式 题 3
如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.
证明:在Rt△ABE和Rt△CBF中,∠ABE=∠CBF=90°,
∵AB=CB,AE=CF ,
∴Rt△ABE≌Rt△CBF(HL).
巩固练习
例2 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF. 即BC=BE.
探究新知
探究新知
方法点拨
证明线段相等可通过证明三角形全等解决,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
如图,已知AE⊥BC,DF⊥BC,E,F是垂足,AE=DF,AB=DC,求证:AC=DB.
证明:AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°.
在Rt△ABE和Rt△DCF中, AE=DF , AB=DC,
∴Rt△ABE≌Rt△DCF(HL),
∴∠ABC=∠DCB.
在△ABC和△DCB中, AB=DC,∠ABC=∠DCB, BC =CB,
∴△ABC≌△DCB(SAS),
∴AC=DB .
巩固练习
例3 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF(全等三角形对应角相等).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
探究新知
利用直角三角形全等解决实际问题
素养考点 2
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
所以Rt△ABD≌Rt△ACD.(HL)
所以BD=CD.
解:BD=CD.
因为∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
AB=AC,
AD=AD,
巩固练习
1.如图,∠A=∠D=90°,AC=DB,AC,DB相交于点O.
求证:OB=OC.
证明:在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
连接中考
证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,
∴∠AED=∠CFD=90°,
∵D为AC的中点,∴AD=DC,
在Rt△ADE和Rt△CDF中,,
∴Rt△ADE≌Rt△CDF,
∴∠A=∠C,∴BA=BC,∵AB=AC,
∴AB=BC=AC,
∴△ABC是等边三角形.
2.已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.
连接中考
D
1. 判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
课堂检测
基础巩固题
2. 如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点
E ,AD、CE交于点H,已知EH=EB=3,AE=4,
则 CH的长为( )
A.1 B.2 C.3 D.4
3.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等”),根据 (用简写法).
全等
HL
课堂检测
A
4. 如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明:∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴ Rt△EBC≌Rt△DCB (HL).
课堂检测
如图,AB=CD, BF⊥AC,DE⊥AC, AE=CF.求证:BF=DE.
证明: ∵ BF⊥AC,DE⊥AC,
∴∠BFA=∠DEC=90 °.
∵AE=CF,
∴AE+EF=CF+EF.即AF=CE.
在Rt△ABF和Rt△CDE中,
AB=CD,
AF=CE.
∴ Rt△ABF≌Rt△CDE(HL).
A
F
C
E
D
B
∴BF=DE.
能力提升题
课堂检测
如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P,Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
拓广探索题
课堂检测
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm,
∴当AP=5cm或10cm时,△ABC才能和△APQ全等.
课堂检测
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm;
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
课堂小结
