人教版数学八年级上册 第十二章 三角形全等的判定(一) SSS 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册 第十二章 三角形全等的判定(一) SSS 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 545.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 16:09:24 | ||
图片预览





文档简介
(共21张PPT)
第十二章 全等三角形
第11课时 三角形全等的判定(一)——SSS
目录
01
本课目标
02
课堂导练
1.构建三角形全等条件的探索思路,体会研究几何问题的方法.
2.探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等.
3.会用尺规作一个角等于已知角,了解作图的道理.
本课目标
知识重点
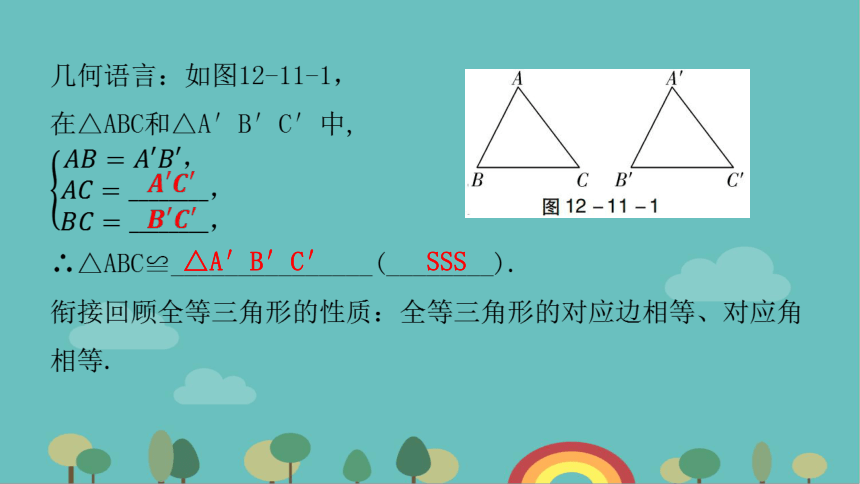
知识点一:三角形全等的判定(SSS)
________分别相等的两个三角形全等(可以简写成“________”或“________”).
三边
边边边
SSS
△A′B′C′
SSS
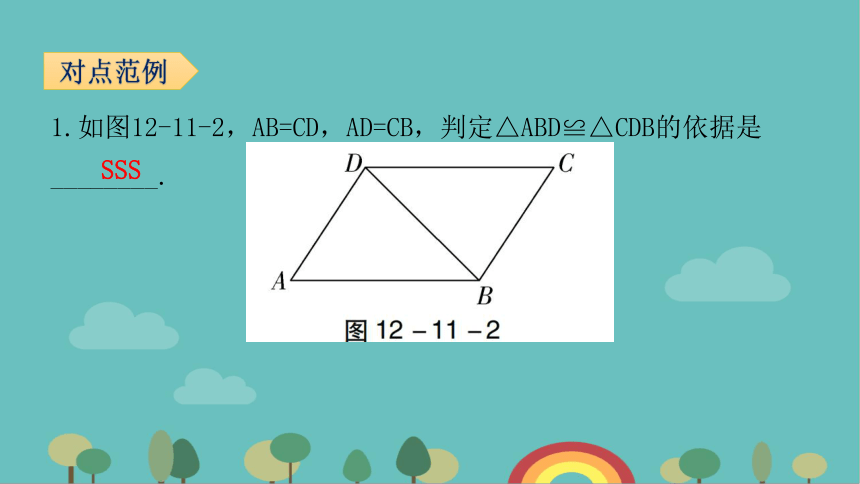
1.如图12-11-2,AB=CD,AD=CB,判定△ABD≌△CDB的依据是________.
对点范例
SSS
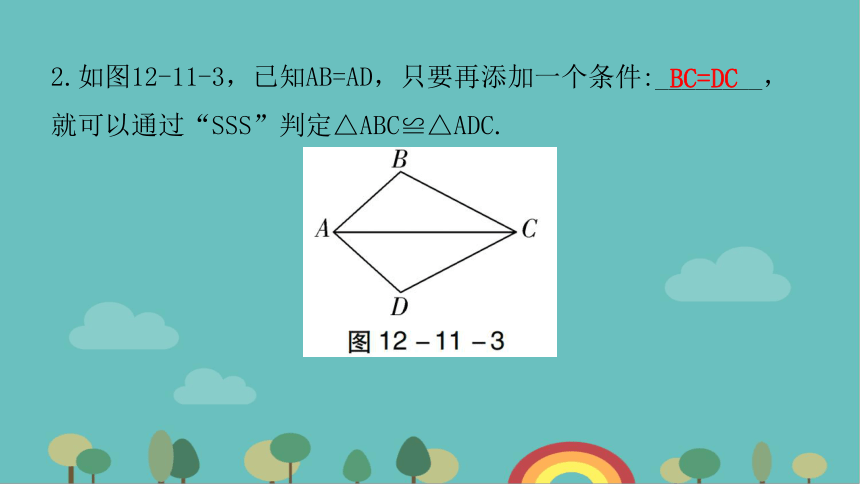
2.如图12-11-3,已知AB=AD,只要再添加一个条件:________,就可以通过“SSS”判定△ABC≌△ADC.
BC=DC
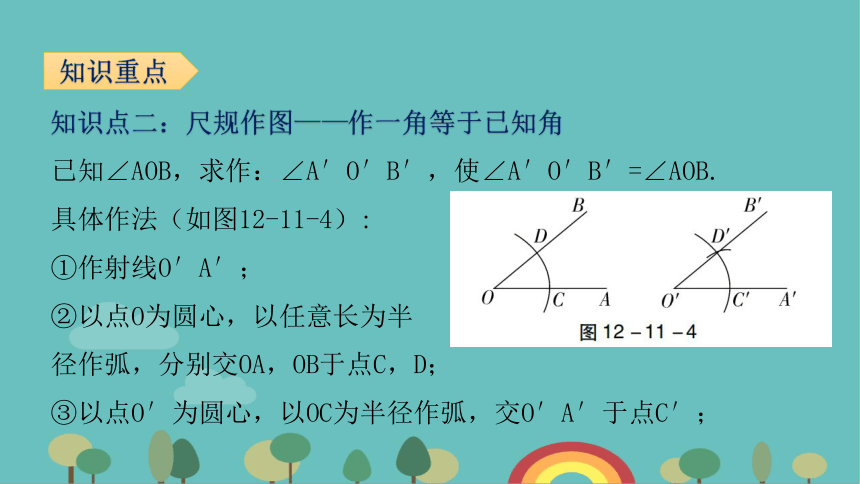
知识点二:尺规作图——作一角等于已知角
已知∠AOB,求作:∠A′O′B′,使∠A′O′B′=∠AOB.
具体作法(如图12-11-4):
①作射线O′A′;
②以点O为圆心,以任意长为半
径作弧,分别交OA,OB于点C,D;
③以点O′为圆心,以OC为半径作弧,交O′A′于点C′;
知识重点
④以点C′为圆心,以CD为半径作弧,交O′B′于点D′;
⑤经过点D′作射线O′B′,则∠A′O′B′就是所作的角.
注意:此处主要为了解作图的原理,实际尺规作图中只需保留作图的痕迹,不要求写出作法.
3.仔细观察用直尺和圆规作一个角等于已知角的示意图(图12-11-5),请根据三角形全等有关知识,说明作出∠CPD=∠AOB的依据是________.
对点范例
SSS
4.如图12-11-6,已知∠α,用尺规作图作∠AOC=∠α.(不写作法,保留作图痕迹)
解:如答图12-11-1,∠AOC即为所作.
课堂导练
【例1】(人教八上P36改编)如图12-11-7,在△ABC
中,AB=AC,D是BC的中点.求证:△ABD≌△ACD.
思路点拨:根据已知条件和图中条件,利用“SSS”即可证明三角形全等.
典型例题
1.如图12-11-8,点A,F,E,D在同一条直线上,AB=DC,BE=CF,AF=DE.求证:△ABE≌△DCF.
举一反三
【例2】(人教八上P44、北师七下P111改编)如图12-11-9,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
典型例题
思路点拨:欲证∠A=∠D,只要证明△ABC≌△DEF即可,关键是正确寻找全等三角形全等的条件.
2.(创新题)如图12-11-10,点E,F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD交于点O.求证:AE∥CF.
举一反三
【例3】(人教八上P37)工人师傅常用角尺平分一个任意角,做法如下:如图12-11-11,∠AOB是一个任意角,
在边OA,OB上分别取OM=ON,移动角尺,使角尺
两边相同的刻度分别与M,N重合,过角尺顶点P
的射线OP便是∠AOB的平分线.为什么?
典型例题
思路点拨:本题通过三角形的全等得到∠BOP和∠AOP相等,从而得到结论.
3.小明制作的风筝形状如图12-11-12,他根据DE=DF,EH=FH,不用测量就知道∠E=∠F,请你运用所学知识给予证明.
举一反三
谢 谢
第十二章 全等三角形
第11课时 三角形全等的判定(一)——SSS
目录
01
本课目标
02
课堂导练
1.构建三角形全等条件的探索思路,体会研究几何问题的方法.
2.探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等.
3.会用尺规作一个角等于已知角,了解作图的道理.
本课目标
知识重点
知识点一:三角形全等的判定(SSS)
________分别相等的两个三角形全等(可以简写成“________”或“________”).
三边
边边边
SSS
△A′B′C′
SSS
1.如图12-11-2,AB=CD,AD=CB,判定△ABD≌△CDB的依据是________.
对点范例
SSS
2.如图12-11-3,已知AB=AD,只要再添加一个条件:________,就可以通过“SSS”判定△ABC≌△ADC.
BC=DC
知识点二:尺规作图——作一角等于已知角
已知∠AOB,求作:∠A′O′B′,使∠A′O′B′=∠AOB.
具体作法(如图12-11-4):
①作射线O′A′;
②以点O为圆心,以任意长为半
径作弧,分别交OA,OB于点C,D;
③以点O′为圆心,以OC为半径作弧,交O′A′于点C′;
知识重点
④以点C′为圆心,以CD为半径作弧,交O′B′于点D′;
⑤经过点D′作射线O′B′,则∠A′O′B′就是所作的角.
注意:此处主要为了解作图的原理,实际尺规作图中只需保留作图的痕迹,不要求写出作法.
3.仔细观察用直尺和圆规作一个角等于已知角的示意图(图12-11-5),请根据三角形全等有关知识,说明作出∠CPD=∠AOB的依据是________.
对点范例
SSS
4.如图12-11-6,已知∠α,用尺规作图作∠AOC=∠α.(不写作法,保留作图痕迹)
解:如答图12-11-1,∠AOC即为所作.
课堂导练
【例1】(人教八上P36改编)如图12-11-7,在△ABC
中,AB=AC,D是BC的中点.求证:△ABD≌△ACD.
思路点拨:根据已知条件和图中条件,利用“SSS”即可证明三角形全等.
典型例题
1.如图12-11-8,点A,F,E,D在同一条直线上,AB=DC,BE=CF,AF=DE.求证:△ABE≌△DCF.
举一反三
【例2】(人教八上P44、北师七下P111改编)如图12-11-9,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
典型例题
思路点拨:欲证∠A=∠D,只要证明△ABC≌△DEF即可,关键是正确寻找全等三角形全等的条件.
2.(创新题)如图12-11-10,点E,F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD交于点O.求证:AE∥CF.
举一反三
【例3】(人教八上P37)工人师傅常用角尺平分一个任意角,做法如下:如图12-11-11,∠AOB是一个任意角,
在边OA,OB上分别取OM=ON,移动角尺,使角尺
两边相同的刻度分别与M,N重合,过角尺顶点P
的射线OP便是∠AOB的平分线.为什么?
典型例题
思路点拨:本题通过三角形的全等得到∠BOP和∠AOP相等,从而得到结论.
3.小明制作的风筝形状如图12-11-12,他根据DE=DF,EH=FH,不用测量就知道∠E=∠F,请你运用所学知识给予证明.
举一反三
谢 谢
