2022—2023学年北师大版数学九年级上册 1.1 菱形的判定 课件(共19张PPT)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级上册 1.1 菱形的判定 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 928.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 17:08:36 | ||
图片预览



文档简介
(共19张PPT)
第一章 特殊平行四边形
学练优九年级数学上(BS)
教学课件
1.1 菱形的判定
3个判定定理+1个推论
学习目标
1.经历菱形判定定理的探究过程,掌握菱形的3个判定定理 (重点)
2.会用这些菱形的判定方法进行有关的证明和计算. (难点)
一、旧知回顾
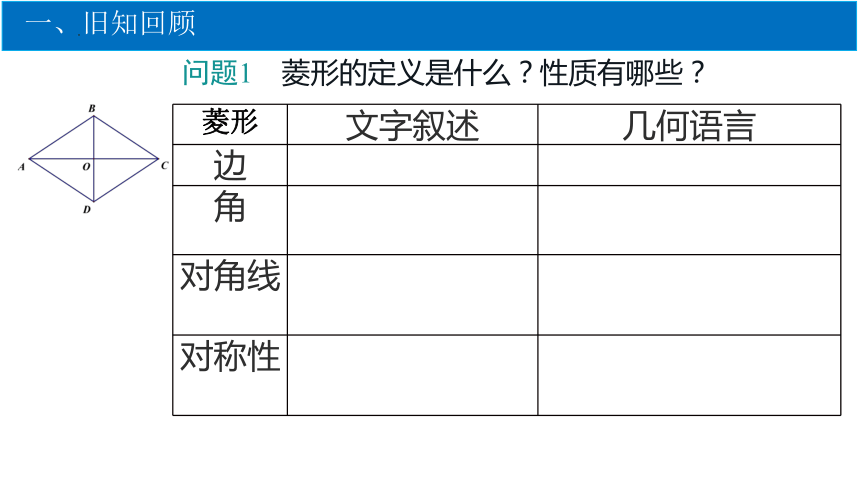
问题1 菱形的定义是什么?性质有哪些?
菱形 文字叙述 几何语言
边
角
对角线
对称性
一、旧知回顾
问题2 有了前面平行四边形的学习基础,你觉得接下来
我们得研究菱形什么方面的知识?
问题3 菱形的判定与它的性质之间有什么样的关系?
学习完菱形的定义、性质,再学习判定
互为逆命题
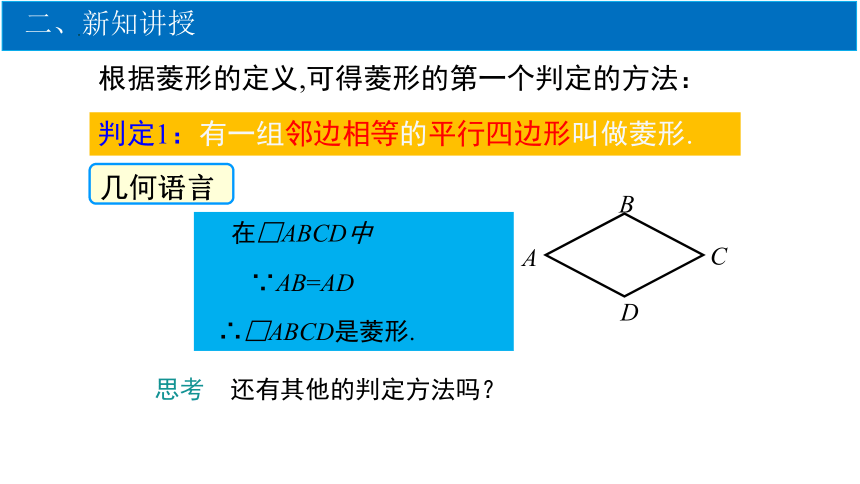
根据菱形的定义,可得菱形的第一个判定的方法:
∵AB=AD
∴□ABCD是菱形.
判定1:有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
思考 还有其他的判定方法吗?
在□ABCD中
二、新知讲授
几何语言
二、新知讲授
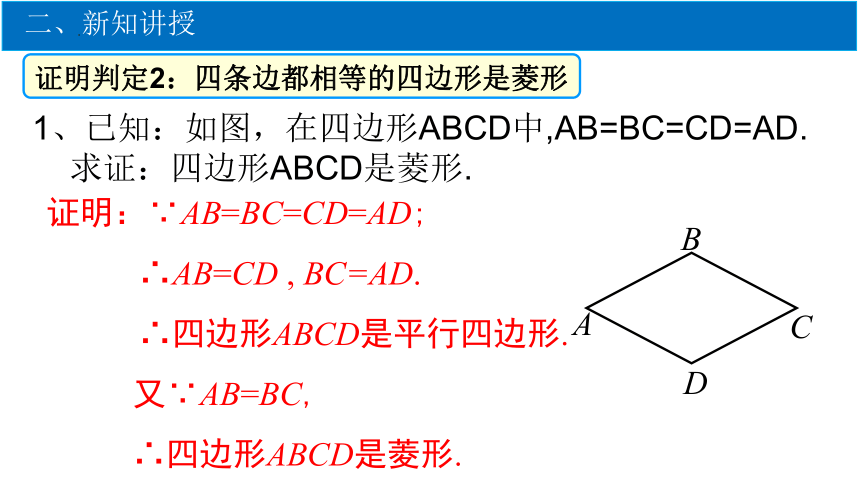
1、已知:如图,在四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明判定2:四条边都相等的四边形是菱形
A
B
C
D
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
AB=BC=CD=AD
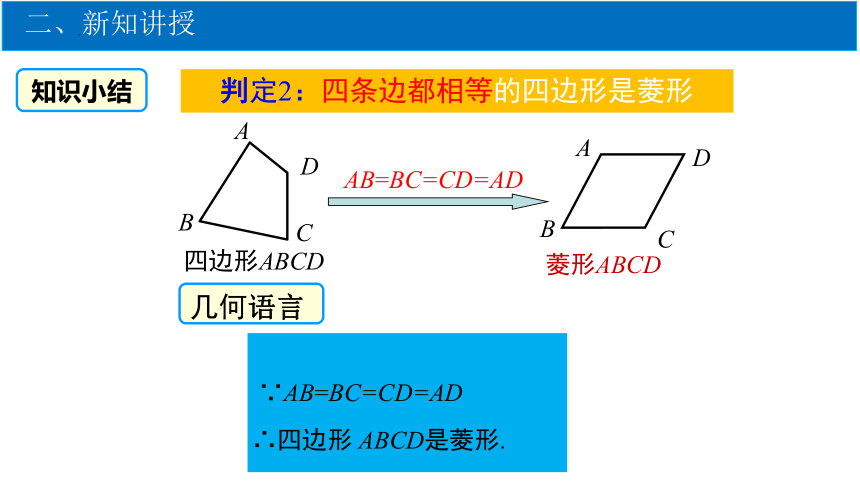
∵AB=BC=CD=AD
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
知识小结
四边形ABCD
A
B
C
D
判定2:四条边都相等的四边形是菱形
二、新知讲授
几何语言
二、新知讲授
已知:如图,在菱形 ABCD 中,对角线 AC 与 BD 相交于点 O,点 E,F,G,H 分别 是 OA,OB,OC,OD 的中点.求证:四边形 EFGH 是菱形
练一练
二、新知讲授
你能利用尺规作图自己画一个菱形吗 试一试吗
用一用
分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.
C
A
B
二、新知讲授
2、已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.
证明判定3:对角线互相垂直的平行四边形是菱形
AC⊥BD
在□ABCD中
∵AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
知识小结
判定3:对角线互相垂直的平行四边形是菱形
几何语言
二、新知讲授
二、新知讲授
巩固练习2:已知:如图,□ABCD的两条对角线AC、BD相交于点O,AB=,AO=2,BO=1.
求证:□ABCD是菱形.
用一用
二、新知讲授
3、已知:如图,AC与BD是四边形ABCD的对角线,OA=OC,OB=OD,AC⊥BD.
求证:□ABCD是菱形.
证明判定3的推论:对角线互相垂直平分的四边形是菱形
AC⊥BD
OA=OC
OB=OD
∵OA=OC OB=OD
∴ 四边形ABCD是平行四边形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
知识小结
判定3的推论:对角线互相垂直平分的四边形是菱形
几何语言
二、新知讲授
四边形ABCD
A
B
C
D
∴ □ABCD是菱形
∵AC⊥BD
五、课堂小结
本节课的主要内容是什么?
你有什么收获和困惑?
三、课堂小结
菱形判定 文字叙述 几何语言
边 判定1:有一组____相等的平行四边形是菱形(定义法)
判定2:_______相等的四边形是菱形
对角线 判定3: 对角线互相_____的平行四边形是菱形
判定3的推论:对角线互相__________四边形是菱形
四、课堂练习
1.菱形 ABCD 的周长为 40 cm,它的一条对角线长 10 cm. (1)求这个菱形的每一个内角的度数; (2)求这个菱形另一条对角线的长.
四、课堂练习
2. 已知:如图,在四边形 ABCD 中,AD = BC,
点 E,F,G,H 分别是 AB,CD,AC,
BD 的中点.求证:四边形 EGFH 是菱形.
四、课堂练习
3.已知:如图,在□ ABCD中,对角线AC的垂直平分线
分别与 AD,AC,BC相交于点 E,O,F.
求证:四边形 AFCE 是菱形.
第一章 特殊平行四边形
学练优九年级数学上(BS)
教学课件
1.1 菱形的判定
3个判定定理+1个推论
学习目标
1.经历菱形判定定理的探究过程,掌握菱形的3个判定定理 (重点)
2.会用这些菱形的判定方法进行有关的证明和计算. (难点)
一、旧知回顾
问题1 菱形的定义是什么?性质有哪些?
菱形 文字叙述 几何语言
边
角
对角线
对称性
一、旧知回顾
问题2 有了前面平行四边形的学习基础,你觉得接下来
我们得研究菱形什么方面的知识?
问题3 菱形的判定与它的性质之间有什么样的关系?
学习完菱形的定义、性质,再学习判定
互为逆命题
根据菱形的定义,可得菱形的第一个判定的方法:
∵AB=AD
∴□ABCD是菱形.
判定1:有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
思考 还有其他的判定方法吗?
在□ABCD中
二、新知讲授
几何语言
二、新知讲授
1、已知:如图,在四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明判定2:四条边都相等的四边形是菱形
A
B
C
D
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
AB=BC=CD=AD
∵AB=BC=CD=AD
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
知识小结
四边形ABCD
A
B
C
D
判定2:四条边都相等的四边形是菱形
二、新知讲授
几何语言
二、新知讲授
已知:如图,在菱形 ABCD 中,对角线 AC 与 BD 相交于点 O,点 E,F,G,H 分别 是 OA,OB,OC,OD 的中点.求证:四边形 EFGH 是菱形
练一练
二、新知讲授
你能利用尺规作图自己画一个菱形吗 试一试吗
用一用
分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.
C
A
B
二、新知讲授
2、已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.
证明判定3:对角线互相垂直的平行四边形是菱形
AC⊥BD
在□ABCD中
∵AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
知识小结
判定3:对角线互相垂直的平行四边形是菱形
几何语言
二、新知讲授
二、新知讲授
巩固练习2:已知:如图,□ABCD的两条对角线AC、BD相交于点O,AB=,AO=2,BO=1.
求证:□ABCD是菱形.
用一用
二、新知讲授
3、已知:如图,AC与BD是四边形ABCD的对角线,OA=OC,OB=OD,AC⊥BD.
求证:□ABCD是菱形.
证明判定3的推论:对角线互相垂直平分的四边形是菱形
AC⊥BD
OA=OC
OB=OD
∵OA=OC OB=OD
∴ 四边形ABCD是平行四边形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
知识小结
判定3的推论:对角线互相垂直平分的四边形是菱形
几何语言
二、新知讲授
四边形ABCD
A
B
C
D
∴ □ABCD是菱形
∵AC⊥BD
五、课堂小结
本节课的主要内容是什么?
你有什么收获和困惑?
三、课堂小结
菱形判定 文字叙述 几何语言
边 判定1:有一组____相等的平行四边形是菱形(定义法)
判定2:_______相等的四边形是菱形
对角线 判定3: 对角线互相_____的平行四边形是菱形
判定3的推论:对角线互相__________四边形是菱形
四、课堂练习
1.菱形 ABCD 的周长为 40 cm,它的一条对角线长 10 cm. (1)求这个菱形的每一个内角的度数; (2)求这个菱形另一条对角线的长.
四、课堂练习
2. 已知:如图,在四边形 ABCD 中,AD = BC,
点 E,F,G,H 分别是 AB,CD,AC,
BD 的中点.求证:四边形 EGFH 是菱形.
四、课堂练习
3.已知:如图,在□ ABCD中,对角线AC的垂直平分线
分别与 AD,AC,BC相交于点 E,O,F.
求证:四边形 AFCE 是菱形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
