人教版2022-2023学年七年级数学上册 2.1.2 单项式 课件(共24张PPT)
文档属性
| 名称 | 人教版2022-2023学年七年级数学上册 2.1.2 单项式 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 17:16:06 | ||
图片预览








文档简介
(共24张PPT)
单 项 式
1.理解单项式、单项式的系数和次数的概念.(重点)
2.会用单项式表示简单的数量关系.(难点)
用含有字母的式子填空,并观察特点:
1.边长为m的正方形的周长为____,面积为____.
3.一辆汽车的速度是vkm/h,它t小时的行驶路程为 km.
2.铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价
是 元.
vt
2.5x
m2
4m
4.半径为r cm的圆的周长是 cm,面积为 cm2.
2πr
πr2
观察列出的式子有什么共同特点
4m
vt
m2
2.5x
数×
字母
v×t
2.5×x
2πr
πr2
m×m
数×
字母
数×
字母
注意: 是圆周率的代号,不是字母.
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示数字与字母、字母与字母的积).
表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
例1.在式子,,,,,,中,单项式
有( )
A.3个 B.4个 C.5个 D.6个
【分析】解:是一个数字,是单项式;3x-y 式子中存在减法运算,不是单项式;
2 x y是数字与字母的乘积,是单项式;a是单独的一个字母是单项式;
式子中存在加法运算,不是单项式;πa2是单项式;
x+1式子中存在加法运算,不是单项式;故单项式一共有4个.
故选:B
B
下列各式中单项式有____________________.
①x-7;②;③4ab;④;⑤;⑥y;⑦;⑧;⑨;
⑩; ; ; -1.
②③⑥
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
判断一个式子是否是单项式,应从哪些方面入手?
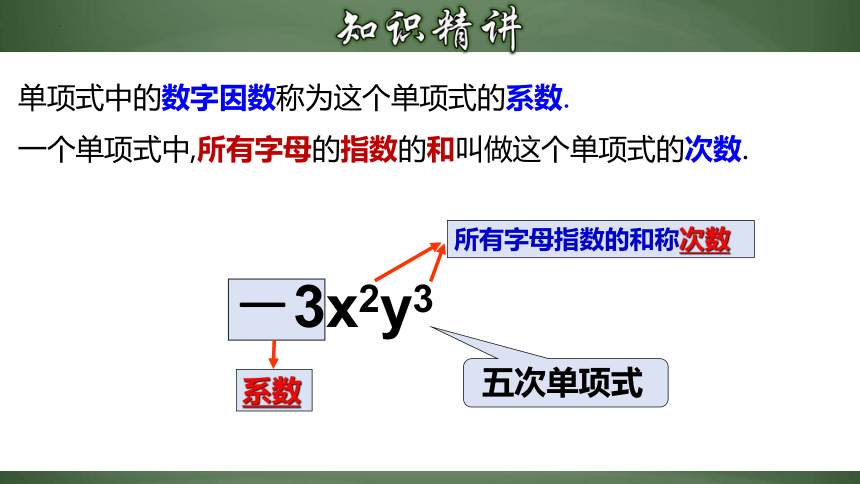
-3x2y3
系数
所有字母指数的和称次数
五次单项式
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1. 每包书有12册,n包书有_____册;
2. 底边长为a,高为h的三角形的面积是_____;
3. 一个长方体的长和宽都是a,高为h,它的体积是_____;
4. 一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价
为____;
5. 一个长方形的长为0.9,宽为a,面积是____.
例2.用单项式填空,并指出它们的系数和次数.
12n
0.9a
0.9a
一次
二次
三次
一次
一次
12
1
0.9
0.9
用字母表示数后,同一个式子可以表示不同的含义.例如,在例3的第(4) (5)小题中,0. 9b既可以表示电视机的售价,又可以表示长方形的面积,当然它还可以表示更多的含义,你能赋予0.9b一个含义吗
1.单项式的系数是______,次数是_______.
2.单项式的系数是______,次数是_______.
3.单项式的系数是______,次数是__________.
4.请你写出一个系数为3,次数为4,只含字母a、b的单项式:________.
-
四次
-
四次
-
六次
3ab3
在研究单项式的系数和次数问题时,要注意哪些问题:
2.圆周率π是常数.
3.单项式的系数应包括它前面的性质符号.
1.当单项式的系数是1或-1时,“1”通常省略不写.
系数问题
4.当单项式的系数不容易看出时,一定要先将单项式写成数×字母的形式.
次数问题
1.切记所有字母的指数的和.
2.当字母指数为1时,不要忽略.
=
例3.若是关于,的五次单项式且系数为6,试求,的值.
解: 是关于,的五次单项式且系数为6,
已知单项式与的次数相同,求的值.
解:由题意得,2+m+2=2+4,
解得m=2.
例4.观察下列各式:﹣a,a2,﹣a3,a4,﹣a5,a6,…
(1)写出第2014个和2015个单项式;
(2)写出第n个单项式.
解:由﹣a,a2,﹣a3,a4,﹣a5,a6,…
可得第n项的表达式为(﹣1)n,
所以第2014个单项式为,第2015个单项式为﹣.
(2)由单项式的特点可得第n个单项式为(﹣1)n.
观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:(1)∵当n=1时,xy,当n=2时,﹣3x2y,当n=3时,5x3y,当n=4时,﹣7x4y,当n=5时,9x5y,
∴第10个单项式是﹣(2×10﹣1) x10y,即﹣19x10y.
第2020个单项式是﹣(2×2020﹣1) x2020y,即﹣4039x2020y.
观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:∵n为奇数时,单项式的系数为正数,n为偶数时,单项式的系数为负数.
∴符合可用(﹣1)n+1表示,
∵系数的数字部分是连续的奇数,
∴可用2n﹣1来表示,
又∵第n个单项式的x的指数为n,y的指数不变,还是1,
∴第n个单项式可表示为(﹣1)n+1(2n﹣1)xny.
1、填表:
-2
五
1
四
二
0.2
二
八
2.-2x2y的系数是_____,次数是______.
3.的系数是______,次数是______.
4.若单项式台xmy2的次数是5,则m=____.
5.如果单项式头amb2n(m,n均为正整数)为六次单项式,那么m可以取的值为________,n可以取的值为________.
-2
三
-
四
3
4或2
1或2
6.下列各式x2y,-mn,0.5,3s-1,0,m,中,单项式的有( )
A.4个 B.5个 C.6个 D.7个
7.单项式-3πxy2z3的系数和次数分别是( )
A.-π,5 B.-1,6 C.-3π,6 D.-3,7
8.关于单项式-23x2y2z, 下列结论中正确的是( )
A.系数是-2,次数是4 B.系数是-2,次数是5
C.系数是-2,次数是8 D.系数是-23,次数是5
B
C
D
9.按一定规律排列的单项式:2x,-3x2,4x3,-5x4,6x5,-7x6,…第n个单项式是( )
A.
B.
C.
D.
D
10.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
解:因为x2y|a|+(b+2)是关于x,y的五次单项式,
所以b+2=0,2+=5
所以a=±3,b=-2
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
一、单项式的概念:
二、单项式的组成要素:
单 项 式
1.理解单项式、单项式的系数和次数的概念.(重点)
2.会用单项式表示简单的数量关系.(难点)
用含有字母的式子填空,并观察特点:
1.边长为m的正方形的周长为____,面积为____.
3.一辆汽车的速度是vkm/h,它t小时的行驶路程为 km.
2.铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价
是 元.
vt
2.5x
m2
4m
4.半径为r cm的圆的周长是 cm,面积为 cm2.
2πr
πr2
观察列出的式子有什么共同特点
4m
vt
m2
2.5x
数×
字母
v×t
2.5×x
2πr
πr2
m×m
数×
字母
数×
字母
注意: 是圆周率的代号,不是字母.
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示数字与字母、字母与字母的积).
表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
例1.在式子,,,,,,中,单项式
有( )
A.3个 B.4个 C.5个 D.6个
【分析】解:是一个数字,是单项式;3x-y 式子中存在减法运算,不是单项式;
2 x y是数字与字母的乘积,是单项式;a是单独的一个字母是单项式;
式子中存在加法运算,不是单项式;πa2是单项式;
x+1式子中存在加法运算,不是单项式;故单项式一共有4个.
故选:B
B
下列各式中单项式有____________________.
①x-7;②;③4ab;④;⑤;⑥y;⑦;⑧;⑨;
⑩; ; ; -1.
②③⑥
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
判断一个式子是否是单项式,应从哪些方面入手?
-3x2y3
系数
所有字母指数的和称次数
五次单项式
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1. 每包书有12册,n包书有_____册;
2. 底边长为a,高为h的三角形的面积是_____;
3. 一个长方体的长和宽都是a,高为h,它的体积是_____;
4. 一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价
为____;
5. 一个长方形的长为0.9,宽为a,面积是____.
例2.用单项式填空,并指出它们的系数和次数.
12n
0.9a
0.9a
一次
二次
三次
一次
一次
12
1
0.9
0.9
用字母表示数后,同一个式子可以表示不同的含义.例如,在例3的第(4) (5)小题中,0. 9b既可以表示电视机的售价,又可以表示长方形的面积,当然它还可以表示更多的含义,你能赋予0.9b一个含义吗
1.单项式的系数是______,次数是_______.
2.单项式的系数是______,次数是_______.
3.单项式的系数是______,次数是__________.
4.请你写出一个系数为3,次数为4,只含字母a、b的单项式:________.
-
四次
-
四次
-
六次
3ab3
在研究单项式的系数和次数问题时,要注意哪些问题:
2.圆周率π是常数.
3.单项式的系数应包括它前面的性质符号.
1.当单项式的系数是1或-1时,“1”通常省略不写.
系数问题
4.当单项式的系数不容易看出时,一定要先将单项式写成数×字母的形式.
次数问题
1.切记所有字母的指数的和.
2.当字母指数为1时,不要忽略.
=
例3.若是关于,的五次单项式且系数为6,试求,的值.
解: 是关于,的五次单项式且系数为6,
已知单项式与的次数相同,求的值.
解:由题意得,2+m+2=2+4,
解得m=2.
例4.观察下列各式:﹣a,a2,﹣a3,a4,﹣a5,a6,…
(1)写出第2014个和2015个单项式;
(2)写出第n个单项式.
解:由﹣a,a2,﹣a3,a4,﹣a5,a6,…
可得第n项的表达式为(﹣1)n,
所以第2014个单项式为,第2015个单项式为﹣.
(2)由单项式的特点可得第n个单项式为(﹣1)n.
观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:(1)∵当n=1时,xy,当n=2时,﹣3x2y,当n=3时,5x3y,当n=4时,﹣7x4y,当n=5时,9x5y,
∴第10个单项式是﹣(2×10﹣1) x10y,即﹣19x10y.
第2020个单项式是﹣(2×2020﹣1) x2020y,即﹣4039x2020y.
观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:∵n为奇数时,单项式的系数为正数,n为偶数时,单项式的系数为负数.
∴符合可用(﹣1)n+1表示,
∵系数的数字部分是连续的奇数,
∴可用2n﹣1来表示,
又∵第n个单项式的x的指数为n,y的指数不变,还是1,
∴第n个单项式可表示为(﹣1)n+1(2n﹣1)xny.
1、填表:
-2
五
1
四
二
0.2
二
八
2.-2x2y的系数是_____,次数是______.
3.的系数是______,次数是______.
4.若单项式台xmy2的次数是5,则m=____.
5.如果单项式头amb2n(m,n均为正整数)为六次单项式,那么m可以取的值为________,n可以取的值为________.
-2
三
-
四
3
4或2
1或2
6.下列各式x2y,-mn,0.5,3s-1,0,m,中,单项式的有( )
A.4个 B.5个 C.6个 D.7个
7.单项式-3πxy2z3的系数和次数分别是( )
A.-π,5 B.-1,6 C.-3π,6 D.-3,7
8.关于单项式-23x2y2z, 下列结论中正确的是( )
A.系数是-2,次数是4 B.系数是-2,次数是5
C.系数是-2,次数是8 D.系数是-23,次数是5
B
C
D
9.按一定规律排列的单项式:2x,-3x2,4x3,-5x4,6x5,-7x6,…第n个单项式是( )
A.
B.
C.
D.
D
10.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
解:因为x2y|a|+(b+2)是关于x,y的五次单项式,
所以b+2=0,2+=5
所以a=±3,b=-2
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
一、单项式的概念:
二、单项式的组成要素:
