2022-2023学年华师大版数学九年级上册 23.3.1 相似三角形 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年华师大版数学九年级上册 23.3.1 相似三角形 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 18:06:11 | ||
图片预览





文档简介
(共20张PPT)
第23章
图形的相似
23.3 相似三角形
第1课时
1.理解并掌握相似三角形的定义;(重点)
2.掌握由平行线判定两个三角形相似; (重点)
3.经历三角形相似的定义及由平行线判定两个三角形相似的
探究过程.(难点)
学习目标
1.什么叫做相似图形?
两个形状相同(大小可以不同)的平面图形称为相似图形.
2.相似图形的性质有哪些?
对应边成比例、对应角相等.
3.什么叫做相似多边形?什么叫做相似多边形的相似比?
两个边数相同的多边形,如果各边对应成比例,各角对应相等,则称为相似多边形.
对应边的比叫做相似多边形的相似比.
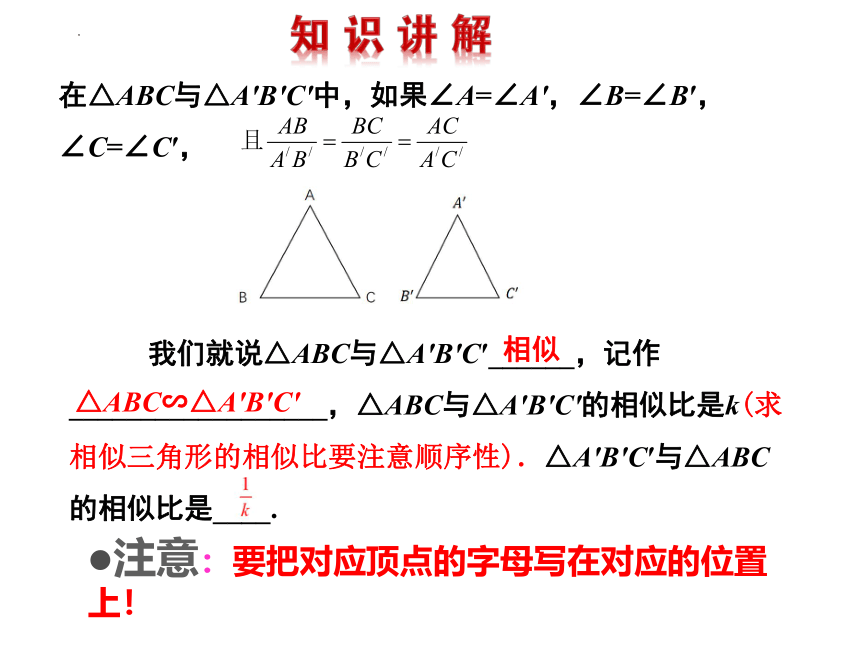
在△ABC与△A′B′C′中,如果∠A=∠A′,∠B=∠B′,∠C=∠C′,
我们就说△ABC与△A′B′C′______,记作__________________,△ABC与△A′B′C′的相似比是k(求相似三角形的相似比要注意顺序性).△A′B′C′与△ABC的相似比是____.
相似
△ABC∽△A′B′C′
注意:要把对应顶点的字母写在对应的位置上!
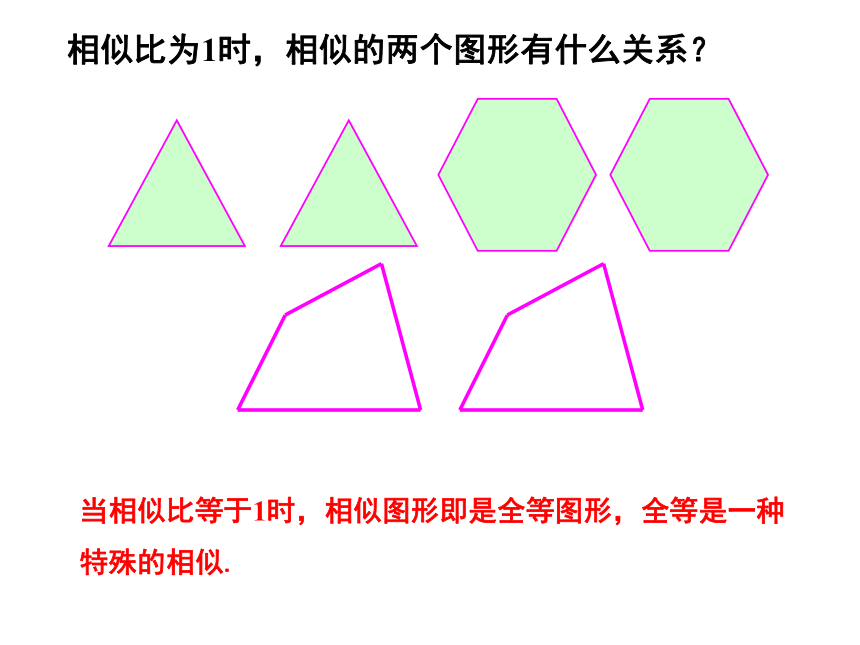
当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似.
相似比为1时,相似的两个图形有什么关系?
基本性质:相似三角形的各对应角相等,各对应边对应成比例.
A
B
C
D
E
F
∵△ ABC∽ △DEF
∴∠A = ∠D,∠B = ∠E,∠C = ∠F.
几何语言:
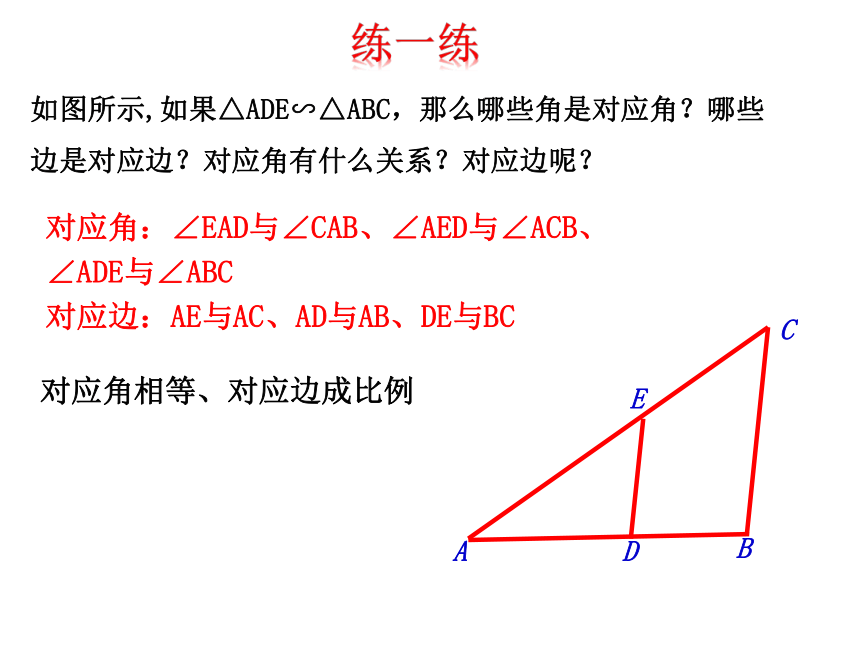
如图所示,如果△ADE∽△ABC,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢?
对应角:∠EAD与∠CAB、∠AED与∠ACB、∠ADE与∠ABC
对应边:AE与AC、AD与AB、DE与BC
A
B
C
D
E
对应角相等、对应边成比例
练一练
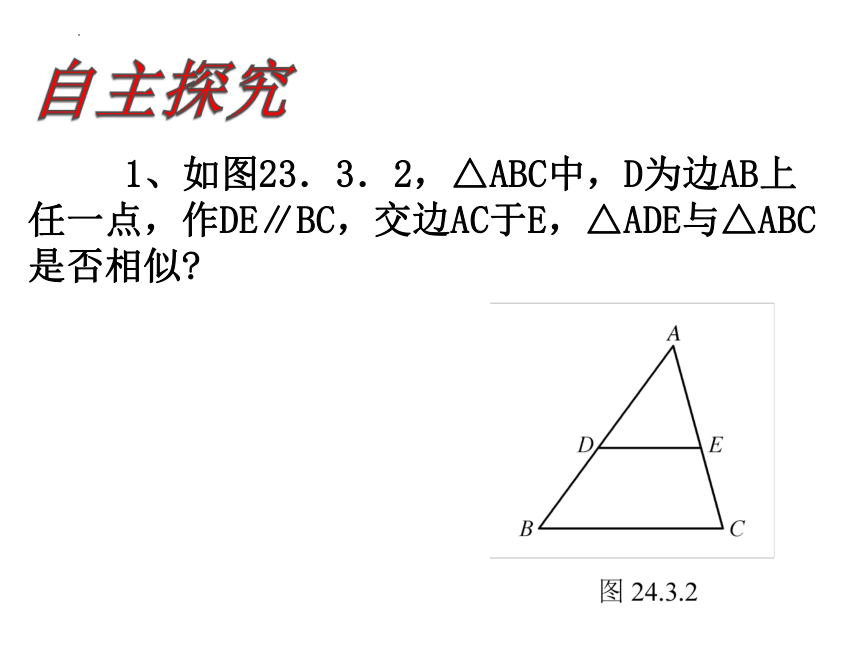
1、如图23.3.2,△ABC中,D为边AB上任一点,作DE∥BC,交边AC于E,△ADE与△ABC是否相似
自主探究
如图,DE∥BC,△ADE与△ABC有什么关系 说明理由.
证明:∵ DE∥BC
∴∠ADE=∠B, ∠AED=∠C,
∴
过E作EF∥AB交BC于F,∴
∴ ∴
∵ DE∥BC,EF∥AB
∴四边形DBFE是平行四边形
∴DE=BF
∴
又∵∠ADE=∠B,∠AED=∠C,∠A=∠A
∴△ADE∽△ABC
定理:平行于三角形一边的直线,和其他两边相交,所构成的三角形与原三角形相似.
2、若是如图DE∥BC,与BO、CO延长线交于D、E,那么△ODE与△OBC还会相似吗 试一试看。如果相似写出它们对应边的比例式.
D
E
O
B
C
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
归纳
【例1】如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5.求BC的长。
【例2】如图,在 ABCD中,E为AB延长线上的一点,AB=3BE,DE与BC相交于点F,请找出图中所有的相似三角形,并求出相应的相似比.
【解析】
∵四边形ABCD是平行四边形,
∴BC∥AD,AB∥CD,
∴△EFB∽△EDA,△EFB∽△DFC,∴△DFC∽△EDA,∵AB=3BE,
∴相似比分别为1∶4,1∶3,3∶4.
一、认真选一选
(1)如图,已知△ABC∽△ACD,则下面哪条线段与AD的比等于相似比( )
A. AD B. BC C. AC D.AB
(2)已知△ABC∽△DEF,点C对应点F,若∠A=30°,∠B=75°,则∠F=( )
A.30° B.75° C.95° D.105°
C
B
(3)下列说法中,正确的是( )
A.直角三角形都相似 B.等腰三角形都相似
C.等边三角形都相似 D.有一组对边平行的两个三角形相似
C
二、填一填:
(1)有两个形状相同的三角形框架,其中一个三角形的三边长分别为4厘米,6厘米和9厘米,另一个三角形的最长边是18厘米,则它的最短边的长是 厘米.
(2)如图,若DE∥BC,AB=9,AC=8,AD=3,则EC的长是 .
(3)如图,平行四边形ABCD中,点E为AD边中点,连接AC、BE交于点F,若AF=4,则AC的长为 .
8
12
三、解答题
如图,在△ABC中,DE∥BC,(1)如果AD=2,DB=3,求DE:BC的值;(2)如果AD=8,DB=12,AC=15,DE=7,求AE和BC的长。
4、如图,四边形 ABCD 是平行四边形,点F在BA的延长线上,连接CF交AD于点E.
(1)求证:△CDE∽△FAE;
当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
课堂小结
1.相似三角形的对应边成比例,对应角相等,相似比等于对应边的比;
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
第23章
图形的相似
23.3 相似三角形
第1课时
1.理解并掌握相似三角形的定义;(重点)
2.掌握由平行线判定两个三角形相似; (重点)
3.经历三角形相似的定义及由平行线判定两个三角形相似的
探究过程.(难点)
学习目标
1.什么叫做相似图形?
两个形状相同(大小可以不同)的平面图形称为相似图形.
2.相似图形的性质有哪些?
对应边成比例、对应角相等.
3.什么叫做相似多边形?什么叫做相似多边形的相似比?
两个边数相同的多边形,如果各边对应成比例,各角对应相等,则称为相似多边形.
对应边的比叫做相似多边形的相似比.
在△ABC与△A′B′C′中,如果∠A=∠A′,∠B=∠B′,∠C=∠C′,
我们就说△ABC与△A′B′C′______,记作__________________,△ABC与△A′B′C′的相似比是k(求相似三角形的相似比要注意顺序性).△A′B′C′与△ABC的相似比是____.
相似
△ABC∽△A′B′C′
注意:要把对应顶点的字母写在对应的位置上!
当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似.
相似比为1时,相似的两个图形有什么关系?
基本性质:相似三角形的各对应角相等,各对应边对应成比例.
A
B
C
D
E
F
∵△ ABC∽ △DEF
∴∠A = ∠D,∠B = ∠E,∠C = ∠F.
几何语言:
如图所示,如果△ADE∽△ABC,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢?
对应角:∠EAD与∠CAB、∠AED与∠ACB、∠ADE与∠ABC
对应边:AE与AC、AD与AB、DE与BC
A
B
C
D
E
对应角相等、对应边成比例
练一练
1、如图23.3.2,△ABC中,D为边AB上任一点,作DE∥BC,交边AC于E,△ADE与△ABC是否相似
自主探究
如图,DE∥BC,△ADE与△ABC有什么关系 说明理由.
证明:∵ DE∥BC
∴∠ADE=∠B, ∠AED=∠C,
∴
过E作EF∥AB交BC于F,∴
∴ ∴
∵ DE∥BC,EF∥AB
∴四边形DBFE是平行四边形
∴DE=BF
∴
又∵∠ADE=∠B,∠AED=∠C,∠A=∠A
∴△ADE∽△ABC
定理:平行于三角形一边的直线,和其他两边相交,所构成的三角形与原三角形相似.
2、若是如图DE∥BC,与BO、CO延长线交于D、E,那么△ODE与△OBC还会相似吗 试一试看。如果相似写出它们对应边的比例式.
D
E
O
B
C
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
归纳
【例1】如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5.求BC的长。
【例2】如图,在 ABCD中,E为AB延长线上的一点,AB=3BE,DE与BC相交于点F,请找出图中所有的相似三角形,并求出相应的相似比.
【解析】
∵四边形ABCD是平行四边形,
∴BC∥AD,AB∥CD,
∴△EFB∽△EDA,△EFB∽△DFC,∴△DFC∽△EDA,∵AB=3BE,
∴相似比分别为1∶4,1∶3,3∶4.
一、认真选一选
(1)如图,已知△ABC∽△ACD,则下面哪条线段与AD的比等于相似比( )
A. AD B. BC C. AC D.AB
(2)已知△ABC∽△DEF,点C对应点F,若∠A=30°,∠B=75°,则∠F=( )
A.30° B.75° C.95° D.105°
C
B
(3)下列说法中,正确的是( )
A.直角三角形都相似 B.等腰三角形都相似
C.等边三角形都相似 D.有一组对边平行的两个三角形相似
C
二、填一填:
(1)有两个形状相同的三角形框架,其中一个三角形的三边长分别为4厘米,6厘米和9厘米,另一个三角形的最长边是18厘米,则它的最短边的长是 厘米.
(2)如图,若DE∥BC,AB=9,AC=8,AD=3,则EC的长是 .
(3)如图,平行四边形ABCD中,点E为AD边中点,连接AC、BE交于点F,若AF=4,则AC的长为 .
8
12
三、解答题
如图,在△ABC中,DE∥BC,(1)如果AD=2,DB=3,求DE:BC的值;(2)如果AD=8,DB=12,AC=15,DE=7,求AE和BC的长。
4、如图,四边形 ABCD 是平行四边形,点F在BA的延长线上,连接CF交AD于点E.
(1)求证:△CDE∽△FAE;
当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
课堂小结
1.相似三角形的对应边成比例,对应角相等,相似比等于对应边的比;
完毕·感谢
The user can perform the presentation on a projector or computer, and the powerpoint can be printed out and made into film.
