安徽省滁州市南谯区施集学校2022-2023学年八年级上学期开学摸底考试数学试卷(含解析)
文档属性
| 名称 | 安徽省滁州市南谯区施集学校2022-2023学年八年级上学期开学摸底考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 535.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 12:09:17 | ||
图片预览



文档简介
2022-2023学年度第一学期八年级开学摸底考试
数学试题
第I卷(选择题 40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数,0.51 ,,,,中,无理数的个数为( )
A.个 B.个 C.个 D.个
2.下列运算正确的是( )
A. B.
C. D.
3.某种粒子的质量为0.00000081g,将0.00000081用科学记数法表示为( )
A. B. C. D.
4.如图,直线、相交于点,,平分,则的度数是( )
A. B. C. D.
5.已知实数a,b,若a>b,则下列结论错误的是( )
A.a-5>b-5 B.3+a>b+3
C. > D.-3a>-3b
6.已知,则的值是( )
A.10 B.15 C.25 D.30
7.关于x的分式方程=﹣1的解是正数,则m的取值范围是( )
A.m>﹣2 B.m<﹣2
C.m>﹣2且m≠2 D.m<﹣2且m≠﹣2
8.如图,直线与相交于点O,,,射线平分,则的度数为( )
A.50° B.60° C.70° D.80°
9.如图所示,已知∠1=∠3,∠2=∠4,不能判定AB∥CD的条件是( )
A.∠1=∠2 B.∠1+∠2=90.
C.∠3+∠4=90. D.∠2+∠3=90.
10.如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点到点的方向平移到三角形的位置,,,,平移距离为7,求阴影部分的面积为( )
A.56 B.54 C.52 D.50
第II卷(非选择题 110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.多项式2x3﹣8x2y+8xy2分解因式的结果是_____.
12.如图,△ABC的边长AB =3 cm,BC=4 cm,AC=2 cm,将△ABC沿BC方向平移a cm(a<4 cm),得到△DEF,连接AD,则阴影部分的周长为_______cm.
13.写出一个比大且比小的整数 _____.
14.已知x的5倍与3的差大于10,且不大于20,用不等式式表示为____________.
三、解答题(本大题共9题,满分90分)
15.(4分)计算:.
16.(6分)先化简,再求值:,其中.
17.(10分)解不等式(组),并把不等式的解集在数轴上表示出来.
(1) (2)
18.(10分)如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,﹣2),B(3,﹣1),C(2,1).
(1)请在图中画出△ABC向左平移4个单位长度的图形△A′B′C′;
(2)写出点B′和C′的坐标.
19.(10分)观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
……
(1)根据以上规律,则(x-1)(x6+x5+x4+x3+x2+x+1)=__________________.
(2)你能否由此归纳出一般性规律(x-1)(xn+xn-1+xn-2+…+x+1)=____________.
(3)根据以上规律求1+3+32+…+349+350的结果.
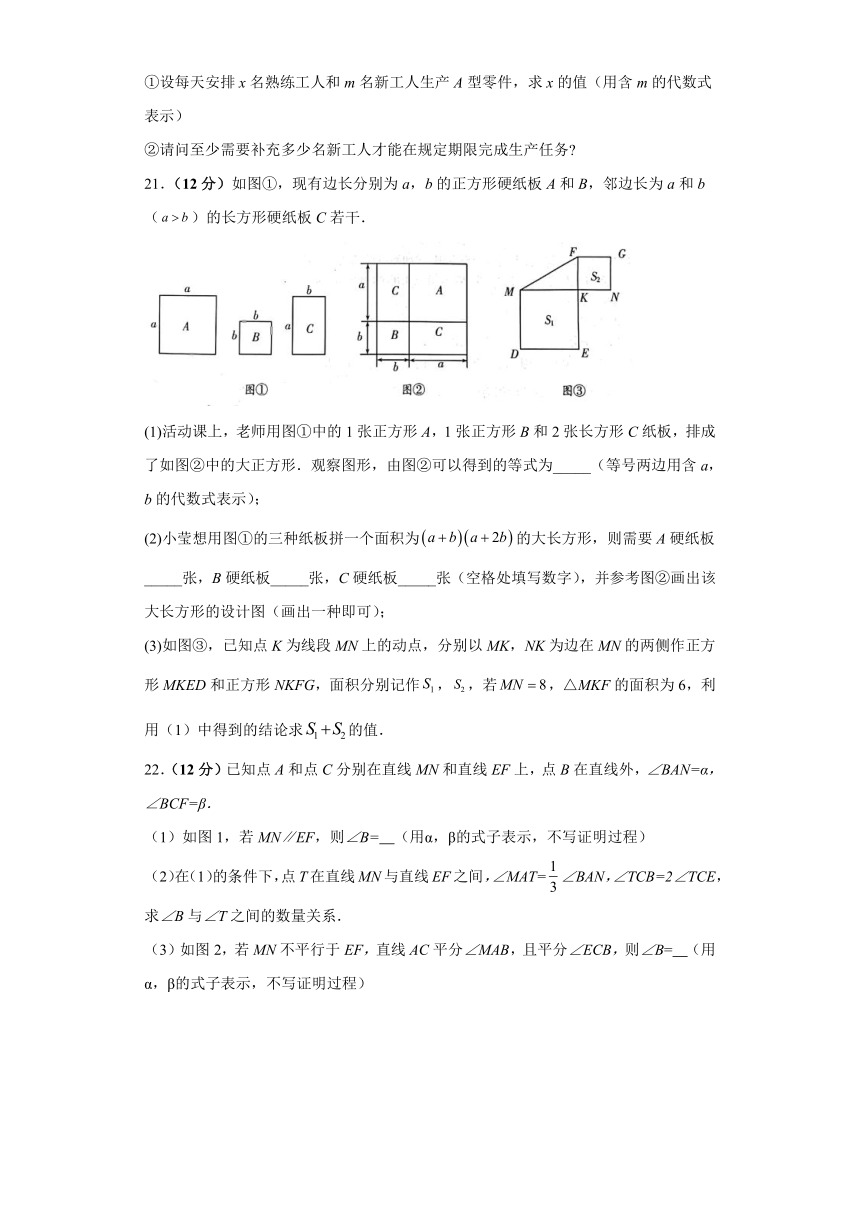
20.(12分)一工厂有60名工人,要完成1200套产品的生产任务,每套产品由4个A型零件和3个B型零件配套组成,每个工人每天能加工6个A型零件或者3个B型零件.现将工人分成两组,每组分别加工一种零件,并要求每天加工的零件正好配套.
(1)工厂每天应安排多少名工人生产A型零件 每天能生产多少套产品
(2)现工厂要在20天内完成1200套产品的生产,决定补充一些新工人,这些新工人只能独立进行A型零件的加工,且每人每天只能加工4个A型零件.
①设每天安排x名熟练工人和m名新工人生产A型零件,求x的值(用含m的代数式表示)
②请问至少需要补充多少名新工人才能在规定期限完成生产任务
21.(12分)如图①,现有边长分别为a,b的正方形硬纸板A和B,邻边长为a和b()的长方形硬纸板C若干.
(1)活动课上,老师用图①中的1张正方形A,1张正方形B和2张长方形C纸板,排成了如图②中的大正方形.观察图形,由图②可以得到的等式为_____(等号两边用含a,b的代数式表示);
(2)小莹想用图①的三种纸板拼一个面积为的大长方形,则需要A硬纸板_____张,B硬纸板_____张,C硬纸板_____张(空格处填写数字),并参考图②画出该大长方形的设计图(画出一种即可);
(3)如图③,已知点K为线段MN上的动点,分别以MK,NK为边在MN的两侧作正方形MKED和正方形NKFG,面积分别记作,,若,△MKF的面积为6,利用(1)中得到的结论求的值.
22.(12分)已知点A和点C分别在直线MN和直线EF上,点B在直线外,∠BAN=α,∠BCF=β.
(1)如图1,若MN∥EF,则∠B= (用α,β的式子表示,不写证明过程)
(2)在(1)的条件下,点T在直线MN与直线EF之间,∠MAT=∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
(3)如图2,若MN不平行于EF,直线AC平分∠MAB,且平分∠ECB,则∠B= (用α,β的式子表示,不写证明过程)
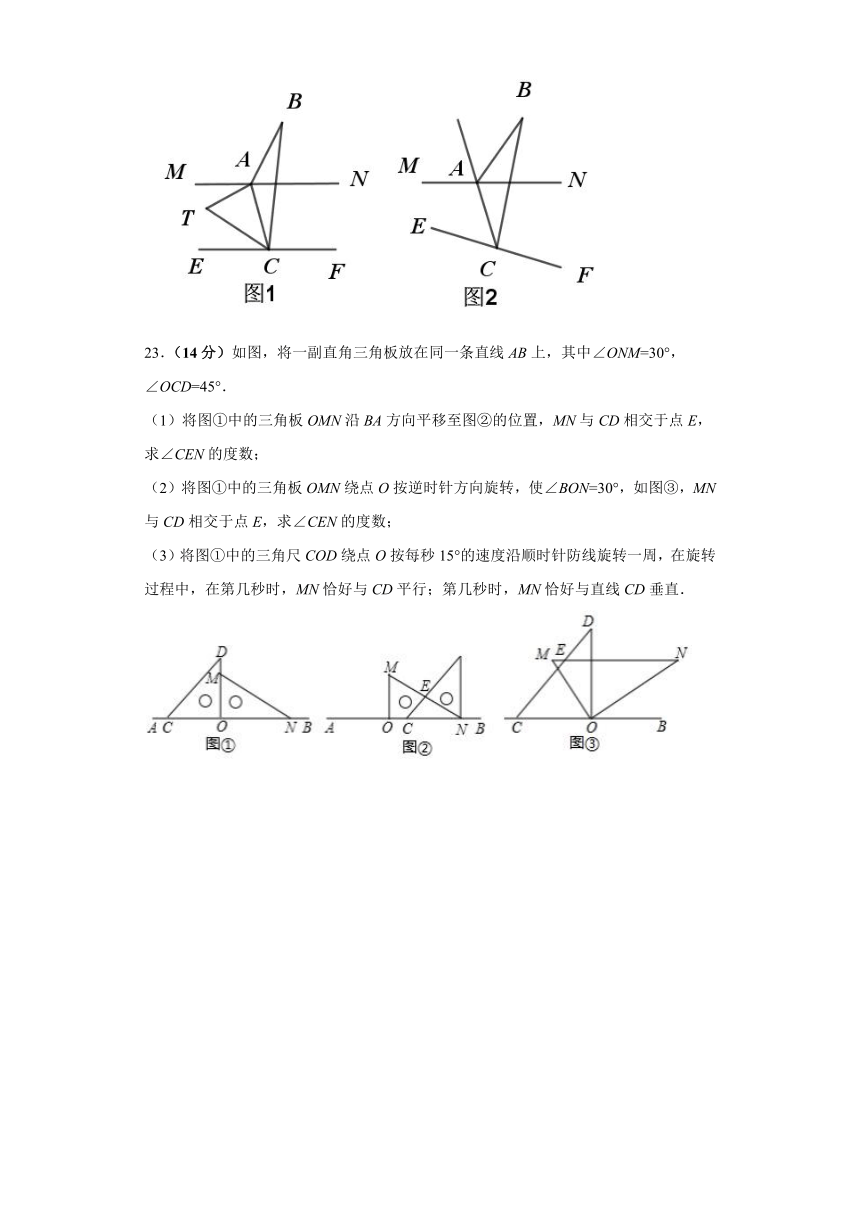
23.(14分)如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角尺COD绕点O按每秒15°的速度沿顺时针防线旋转一周,在旋转过程中,在第几秒时,MN恰好与CD平行;第几秒时,MN恰好与直线CD垂直.
参考答案:
1.B
【解析】
【详解】
在实数, ,,,,中,无理数有 ,,共2个,
故选B.
2.B
【解析】
【分析】
根据同底数幂的乘法的运算法则、完全平方公式、积的乘方的运算法则、合并同类项法则解答即可.
【详解】
解:A、,原计算错误,故此选项不符合题意.
B、,原计算正确,故此选项符合题意;
C、,原计算错误,故此选项不符合题意;
D、,原计算错误,故此选项不符合题意;
故选:B.
【点睛】
此题考查了同底数幂的乘法的运算法则、完全平方公式、积的乘方的运算法则、合并同类项法则,熟练掌握同底数幂的乘法的运算法则、完全平方公式、积的乘方的运算法则、合并同类项法则是解本题的关键.
3.C
【解析】
【分析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
0.00000081=8.1×10-7.
故选C.
【点睛】
考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
4.C
【解析】
【分析】
根据垂线的定义和角平分线的定义可得的度数,再根据平角的定义可得的度数.
【详解】
解:,
,
平分,
,
,
故选:.
【点睛】
此题考查了垂线,角平分线的定义,平角的定义,关键是得到的度数.
5.D
【解析】
【详解】
由不等式性质,选项D. -3a<-3b,所以D错,故选D.
6.C
【解析】
【分析】
,代入求值即可.
【详解】
解:∵,
∴=25.
故选:C.
【点睛】
本题考查已知代数式的值进行求值的计算,熟练掌握平方差公式是解决问题的关键.
7.C
【解析】
【分析】
先解分式方程,用含m的代数式表示出x.再根据方程的解为正数,得到关于m的不等式,求解即可.
【详解】
解:去分母,得x+m﹣2m=2﹣x,
移项,得2x=2+m,
∴x=1+.
由于方程的解是正数,
∴1+>0且1+≠2.
解得m>﹣2且m≠2.
故选:C.
【点睛】
本题考查了分式方程的解、一元一次不等式的解法,掌握解分式方程的一般步骤是解题的关键.
8.B
【解析】
【分析】
首先设∠DOF=2x,∠AOD=3x,然后表示∠FOE和∠BOE,再根据平角定义列方程,然后可得答案.
【详解】
解:设∠DOF=2x,∠AOD=3x,
∵∠DOE=80°,
∴∠FOE=80°﹣2x,
∵射线OE平分∠BOF,
∴∠BOE=∠EOF=80°﹣2x,
则:3x+80°+80°﹣2x=180°,
解得:x=20°,
∴∠AOD=60°
∴∠BOC=∠AOD=60°
故选B.
【点睛】
此题主要考查了邻补角和对顶角,关键是理清图中角之间的关系,利用方程思想解决问题.
9.A
【解析】
【详解】
∵AE平分∠BAC,CE平分∠ACD,∴∠1=∠3,∠2=∠4,
A、∵∠1=∠2,∴∠1+∠3=∠2+∠4,同旁内角相等,并不能判定两直线平行,故错误;
B、∵∠1+∠2=90°,∴∠1+∠2+∠3+∠4=180°,即同旁内角互补,可得其平行,故B正确;
C、D、同B,皆由同旁内角互补,可判定其平行,故C,D都正确.故选A.
10.A
【解析】
【分析】
由三角形ABC的面积等于三角形DEF的面积,推出四边形ABEH的面积等于阴影部分的面积,即可解决问题.
【详解】
由平移的性质知,BE=7,DE=AB=10,
可得HE=DE-DH=10-4=6,
所以S四边形HDFC=S梯形ABEH=(AB+EH)×BE=(10+6)×7=56.
故选:A
【点睛】
此题主要考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点连线的线段平行且相等,对应线段平行且相等,对应角相等,要熟练掌握.
11.2x(x﹣2y)2.
【解析】
【分析】
先提取公因式2x,再利用公式法分解因式.
【详解】
解:2x3﹣8x2y+8xy2=2x(x2﹣4xy+4y2)=2x(x﹣2y)2.
故答案为:2x(x﹣2y)2.
【点睛】
此题考查因式分解的方法,当多项式中的各项有公因式时,先提取公因式,再根据公式法将能分解的因式继续分解,直至不能再分解为止.
12.9
【解析】
【分析】
根据平移的特点,可直接得出AC、DE、AD的长,利用EC=BC-BE可得出EC的长,进而得出阴影部分周长.
【详解】
∵AB=3cm,BC=4cm,AC=2cm,将△ABC沿BC方向平移acm
∴DE=AB=3cm,BE=acm
∴EC=BC-BE=(4-a)cm
∴阴影部分周长=2+3+(4-a)+a=9cm
故答案为:9
【点睛】
本题考查平移的特点和整式的加减计算,解题关键是利用平移的性质,得出EC=BC-BE.
13.3(答案不唯一)
【解析】
【分析】
先对和进行估算,再根据题意即可得出答案.
【详解】
解:∵<2<3<4<,
∴比大且比小的整数有2,3,4.
故答案为:3(答案不唯一).
【点睛】
此题考查了估算无理数的大小,估算出与是解题的关键.
14.10﹤5x-3≤20
【解析】
【分析】
“的倍与的差”中,被减式为的倍,减式为;大于,且小于或等于,应表示为相减得到的相关式子,相减得到的相关式子.
【详解】
解:的倍与的差大于,且不小于,用不等式组表示.
故答案为:.
【点睛】
本题主要考查列一元一次不等式组,解决本题的关键是理解大于用数学符号表示为“”;不大于用数学符号表示为“”.
15.
【解析】
【分析】
根据、去绝对值运算和零指数幂运算分别求解即可.
【详解】
解:
.
【点睛】
本题考查实数的混合运算,涉及到、去绝对值运算和零指数幂运算,熟练掌握相关运算法则是解决问题的关键.
16.
【解析】
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
【详解】
原式,
当时,原式.
【点睛】
此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
17.(1),数轴表示见解析;(2)-2<x≤3,数轴表示见解析
【解析】
【分析】
(1)先求出不等式的解集,再在数轴上表示出来即可;
(2)先求出不等式组的解集,再在数轴上表示出来即可.
【详解】
解:(1)移项得:,
合并同类项得:,
系数化为1得:,
在数轴上表示为:
(2),
解不等式①得:x≤3,
解不等式②得:x>-2,
所以不等式组的解集是:-2<x≤3,
在数轴上表示为:
【点睛】
本题考查了解一元一次不等式,解一元一次不等式组,在数轴上表示不等式或不等式组的解集等知识点,能求出不等式或不等式组的解集是解此题的关键.
18.(1)见解析(2)B′(﹣1,﹣1),C′(﹣2,1).
【解析】
【详解】
试题分析:(1)根据图形平移的性质画出△A′B′C′即可;
(2)根据点B′和C′在坐标系中的位置写出两点坐标即可.
解:(1)如图所示;
(2)由图可知B′(﹣1,﹣1),C′(﹣2,1).
【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.
19.(1)x7-1;(2)xn+1-1;(3).
【解析】
【分析】
(1)仿照已知等式写出答案即可;
(2)先归纳总结出规律,然后按规律解答即可;
(3)先利用得出规律的变形,然后利用规律解答即可.
【详解】
解:(1)根据题意得:(x-1)(x6+x5+x4+x3+x2+x+1)=x7-1;
(2)根据题意得:(x-1)(x"+x"-1+.…+x+1)=x"+1-1;
(3)原式=×(3-1)(1+3+32+···+349+350)= ×(x50+1-1)=
故答案为:(1)x7-1;(2)xn+1-1;(3).
【点睛】
本题考查了平方差公式以及规律型问题,弄清题意、发现数字的变化规律是解答本题的关键.
20.(1)工厂每天应安排24名工人生产A型零件,每天能生产36套产品
(2)①;②至少需要补充60名新工人才能在规定期限完成生产任务
【解析】
【分析】
(1)设工厂每天安排名工人生产A型零件,则工厂每天安排名工人生产B型零件,根据“每套产品由4个A型零件和3个B型零件配套组成”列方程求解即可;
(2)①根据“x名熟练工人和m名新工人生产的A型零件等于1200套产品的A型零件总数”可列方程,进行整理即可;
②设需要补充m名新工人才能在规定期限完成生产任务,安排n名熟练工人生产A型零件,则安排名熟练工人生产B型零件,根据题意,可得关于m、n的方程组,求解即可.
(1)
解:设工厂每天安排名工人生产A型零件,则工厂每天安排名工人生产B型零件,
由题意得:,
解得,
(套)
所以,工厂每天应安排24名工人生产A型零件,每天能生产36套产品.
(2)
①设每天安排x名熟练工人和m名新工人生产A型零件,则安排名熟练工人生产B型零件,
由题意得,,
整理得;
②设需要补充m名新工人才能在规定期限完成生产任务,安排n名熟练工人生产A型零件,则安排名熟练工人生产B型零件,
由题意得,
解得,
所以,至少需要补充60名新工人才能在规定期限完成生产任务.
【点睛】
本题考查了一元一次方程的实际应用,二元一次方程组的实际应用,准确理解题意,熟练掌握知识点是解题的关键.
21.(1)
(2)1,2,3,图见解析
(3)
【解析】
【分析】
(1)用两种方法表示出来面积即可得出等式;
(2)先计算多项式乘以多项式,即可得出需要纸板的数量,然后根据纸板数量画出相应图形即可;
(3)设,,利用(1)中结论进行变形求解即可.
(1)
解:根据图形可得:,
故答案为:
(2)
解:(a+b)(a+2b)=,
需要A硬纸板1张,B硬纸板2张,C硬纸板3张,
故答案为:1,2,3;
设计图可以为:
a ab ab ab ab
b a ab
ab
a b b a b b
(3)
设,
由题意得:,
由(1)知:
∴
即.
【点睛】
本题主要考查多项式乘法与图形面积的关系,熟练掌握多项式乘以多项式的计算方法及面积表示方法是解题关键.
22.(1)β-α;(2)∠ATC=-∠B+60°;(3)∠B=(β-α)
【解析】
【分析】
(1)利用平行线的性质和三角形外角的性质求解即可;
(2)过T作TK∥MN,根据平行线的性质得出∠ATK=∠MAT,∠KTC=∠TCE,再由∠MAT=∠BAN,∠TCB=2∠TCE,表示出∠ATC=-(β-α)+60°,结合∠B=β-α,即可求出结果;
(3)根据题中条件可得:∠BAH=(180°-α),∠BCA=(180°-β),结合∠BAH=∠B+∠BCA,可得∠B.
【详解】
解:(1)如图,设MN与BC交于点G,
∵MN∥EF,
∴∠BGN=∠BCF=β,
∴∠B=∠BGN-∠BAN=β-α,
故答案为:β-α;
(2)如图,过T作TK∥MN,
∵MN∥EF,
∴∠ATK=∠MAT,∠KTC=∠TCE,
∵∠MAT=∠BAN,∠TCB=2∠TCE,
∴∠ATC=∠ATK+∠KTC
=∠MAT+∠TCE
=∠BAN+∠TCB
=α+××(180°-∠BCF)
=α-β+60°
=-(β-α)+60°
∵∠B=β-α,
∴∠ATC=-∠B+60°;
(3)如图,
∵直线AC平分∠MAB,且平分∠ECB,
∴∠BAH=∠MAH=(180°-∠BAN)=(180°-α),
∠BCA=∠ECA=(180°-∠BCF)=(180°-β),
∵∠BAH=∠B+∠BCA,
∴(180°-α)=∠B+(180°-β),
∴∠B=(β-α).
【点睛】
本题综合考查了平行线的性质和三角形外角的性质,以及角平分线的定义,作出适当的辅助线,结合图形进行推理计算是解题的关键.
23.(1) 105°;(2) 135°; (3)5或17;11或23
【解析】
【分析】
(1)根据三角形的内角和定理列式计算即可得解;
(2)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(3)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
【详解】
解:(1)在△CEN中,
∠CEN=180°-∠DCN-∠MNO=180°-45°-30°=105°
(2)∵∠BON=∠N=30°,
∴MN∥CB,
∴∠CEN=180°-∠DCO=180°-45°=135°
(3)如图1,CD在AB上方时,设OM与CD相交于F,
∵CD∥MN,
∴∠OFD=∠M=60°,
在△ODF中,∠MOD=180°-∠D-∠OFD,
=180°-45°-60°,
=75°,
∴旋转角为75°,
t=75°÷15°=5秒;
CD在AB的下方时,设直线OM与CD相交于F,
∵CD∥MN,
∴∠DFO=∠M=60°,
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转角为75°+180°=255°,
t=255°÷15°=17秒;
综上所述,第5或17秒时,边CD恰好与边MN平行;
如图2,CD在OM的右边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGC=90°-∠MNO=90°-30°=60°,
∴∠CON=∠NGC-∠OCD=60°-45°=15°,
∴旋转角为180°-∠CON=180°-15°=165°,
t=165°÷15°=11秒,
CD在OM的左边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGD=90°-∠MNO=90°-30°=60°,
∴∠AOC=∠NGD-∠C=60°-45°=15°,
∴旋转角为360°-∠AOC=360°-15°=345°,
t=345°÷15°=23秒,
综上所述,第11或23秒时,直线CD恰好与直线MN垂直.
【点睛】
本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,难点在于(3)分情况讨论,作出图形更形象直观.
数学试题
第I卷(选择题 40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数,0.51 ,,,,中,无理数的个数为( )
A.个 B.个 C.个 D.个
2.下列运算正确的是( )
A. B.
C. D.
3.某种粒子的质量为0.00000081g,将0.00000081用科学记数法表示为( )
A. B. C. D.
4.如图,直线、相交于点,,平分,则的度数是( )
A. B. C. D.
5.已知实数a,b,若a>b,则下列结论错误的是( )
A.a-5>b-5 B.3+a>b+3
C. > D.-3a>-3b
6.已知,则的值是( )
A.10 B.15 C.25 D.30
7.关于x的分式方程=﹣1的解是正数,则m的取值范围是( )
A.m>﹣2 B.m<﹣2
C.m>﹣2且m≠2 D.m<﹣2且m≠﹣2
8.如图,直线与相交于点O,,,射线平分,则的度数为( )
A.50° B.60° C.70° D.80°
9.如图所示,已知∠1=∠3,∠2=∠4,不能判定AB∥CD的条件是( )
A.∠1=∠2 B.∠1+∠2=90.
C.∠3+∠4=90. D.∠2+∠3=90.
10.如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点到点的方向平移到三角形的位置,,,,平移距离为7,求阴影部分的面积为( )
A.56 B.54 C.52 D.50
第II卷(非选择题 110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.多项式2x3﹣8x2y+8xy2分解因式的结果是_____.
12.如图,△ABC的边长AB =3 cm,BC=4 cm,AC=2 cm,将△ABC沿BC方向平移a cm(a<4 cm),得到△DEF,连接AD,则阴影部分的周长为_______cm.
13.写出一个比大且比小的整数 _____.
14.已知x的5倍与3的差大于10,且不大于20,用不等式式表示为____________.
三、解答题(本大题共9题,满分90分)
15.(4分)计算:.
16.(6分)先化简,再求值:,其中.
17.(10分)解不等式(组),并把不等式的解集在数轴上表示出来.
(1) (2)
18.(10分)如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,﹣2),B(3,﹣1),C(2,1).
(1)请在图中画出△ABC向左平移4个单位长度的图形△A′B′C′;
(2)写出点B′和C′的坐标.
19.(10分)观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
……
(1)根据以上规律,则(x-1)(x6+x5+x4+x3+x2+x+1)=__________________.
(2)你能否由此归纳出一般性规律(x-1)(xn+xn-1+xn-2+…+x+1)=____________.
(3)根据以上规律求1+3+32+…+349+350的结果.
20.(12分)一工厂有60名工人,要完成1200套产品的生产任务,每套产品由4个A型零件和3个B型零件配套组成,每个工人每天能加工6个A型零件或者3个B型零件.现将工人分成两组,每组分别加工一种零件,并要求每天加工的零件正好配套.
(1)工厂每天应安排多少名工人生产A型零件 每天能生产多少套产品
(2)现工厂要在20天内完成1200套产品的生产,决定补充一些新工人,这些新工人只能独立进行A型零件的加工,且每人每天只能加工4个A型零件.
①设每天安排x名熟练工人和m名新工人生产A型零件,求x的值(用含m的代数式表示)
②请问至少需要补充多少名新工人才能在规定期限完成生产任务
21.(12分)如图①,现有边长分别为a,b的正方形硬纸板A和B,邻边长为a和b()的长方形硬纸板C若干.
(1)活动课上,老师用图①中的1张正方形A,1张正方形B和2张长方形C纸板,排成了如图②中的大正方形.观察图形,由图②可以得到的等式为_____(等号两边用含a,b的代数式表示);
(2)小莹想用图①的三种纸板拼一个面积为的大长方形,则需要A硬纸板_____张,B硬纸板_____张,C硬纸板_____张(空格处填写数字),并参考图②画出该大长方形的设计图(画出一种即可);
(3)如图③,已知点K为线段MN上的动点,分别以MK,NK为边在MN的两侧作正方形MKED和正方形NKFG,面积分别记作,,若,△MKF的面积为6,利用(1)中得到的结论求的值.
22.(12分)已知点A和点C分别在直线MN和直线EF上,点B在直线外,∠BAN=α,∠BCF=β.
(1)如图1,若MN∥EF,则∠B= (用α,β的式子表示,不写证明过程)
(2)在(1)的条件下,点T在直线MN与直线EF之间,∠MAT=∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
(3)如图2,若MN不平行于EF,直线AC平分∠MAB,且平分∠ECB,则∠B= (用α,β的式子表示,不写证明过程)
23.(14分)如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角尺COD绕点O按每秒15°的速度沿顺时针防线旋转一周,在旋转过程中,在第几秒时,MN恰好与CD平行;第几秒时,MN恰好与直线CD垂直.
参考答案:
1.B
【解析】
【详解】
在实数, ,,,,中,无理数有 ,,共2个,
故选B.
2.B
【解析】
【分析】
根据同底数幂的乘法的运算法则、完全平方公式、积的乘方的运算法则、合并同类项法则解答即可.
【详解】
解:A、,原计算错误,故此选项不符合题意.
B、,原计算正确,故此选项符合题意;
C、,原计算错误,故此选项不符合题意;
D、,原计算错误,故此选项不符合题意;
故选:B.
【点睛】
此题考查了同底数幂的乘法的运算法则、完全平方公式、积的乘方的运算法则、合并同类项法则,熟练掌握同底数幂的乘法的运算法则、完全平方公式、积的乘方的运算法则、合并同类项法则是解本题的关键.
3.C
【解析】
【分析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
0.00000081=8.1×10-7.
故选C.
【点睛】
考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
4.C
【解析】
【分析】
根据垂线的定义和角平分线的定义可得的度数,再根据平角的定义可得的度数.
【详解】
解:,
,
平分,
,
,
故选:.
【点睛】
此题考查了垂线,角平分线的定义,平角的定义,关键是得到的度数.
5.D
【解析】
【详解】
由不等式性质,选项D. -3a<-3b,所以D错,故选D.
6.C
【解析】
【分析】
,代入求值即可.
【详解】
解:∵,
∴=25.
故选:C.
【点睛】
本题考查已知代数式的值进行求值的计算,熟练掌握平方差公式是解决问题的关键.
7.C
【解析】
【分析】
先解分式方程,用含m的代数式表示出x.再根据方程的解为正数,得到关于m的不等式,求解即可.
【详解】
解:去分母,得x+m﹣2m=2﹣x,
移项,得2x=2+m,
∴x=1+.
由于方程的解是正数,
∴1+>0且1+≠2.
解得m>﹣2且m≠2.
故选:C.
【点睛】
本题考查了分式方程的解、一元一次不等式的解法,掌握解分式方程的一般步骤是解题的关键.
8.B
【解析】
【分析】
首先设∠DOF=2x,∠AOD=3x,然后表示∠FOE和∠BOE,再根据平角定义列方程,然后可得答案.
【详解】
解:设∠DOF=2x,∠AOD=3x,
∵∠DOE=80°,
∴∠FOE=80°﹣2x,
∵射线OE平分∠BOF,
∴∠BOE=∠EOF=80°﹣2x,
则:3x+80°+80°﹣2x=180°,
解得:x=20°,
∴∠AOD=60°
∴∠BOC=∠AOD=60°
故选B.
【点睛】
此题主要考查了邻补角和对顶角,关键是理清图中角之间的关系,利用方程思想解决问题.
9.A
【解析】
【详解】
∵AE平分∠BAC,CE平分∠ACD,∴∠1=∠3,∠2=∠4,
A、∵∠1=∠2,∴∠1+∠3=∠2+∠4,同旁内角相等,并不能判定两直线平行,故错误;
B、∵∠1+∠2=90°,∴∠1+∠2+∠3+∠4=180°,即同旁内角互补,可得其平行,故B正确;
C、D、同B,皆由同旁内角互补,可判定其平行,故C,D都正确.故选A.
10.A
【解析】
【分析】
由三角形ABC的面积等于三角形DEF的面积,推出四边形ABEH的面积等于阴影部分的面积,即可解决问题.
【详解】
由平移的性质知,BE=7,DE=AB=10,
可得HE=DE-DH=10-4=6,
所以S四边形HDFC=S梯形ABEH=(AB+EH)×BE=(10+6)×7=56.
故选:A
【点睛】
此题主要考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点连线的线段平行且相等,对应线段平行且相等,对应角相等,要熟练掌握.
11.2x(x﹣2y)2.
【解析】
【分析】
先提取公因式2x,再利用公式法分解因式.
【详解】
解:2x3﹣8x2y+8xy2=2x(x2﹣4xy+4y2)=2x(x﹣2y)2.
故答案为:2x(x﹣2y)2.
【点睛】
此题考查因式分解的方法,当多项式中的各项有公因式时,先提取公因式,再根据公式法将能分解的因式继续分解,直至不能再分解为止.
12.9
【解析】
【分析】
根据平移的特点,可直接得出AC、DE、AD的长,利用EC=BC-BE可得出EC的长,进而得出阴影部分周长.
【详解】
∵AB=3cm,BC=4cm,AC=2cm,将△ABC沿BC方向平移acm
∴DE=AB=3cm,BE=acm
∴EC=BC-BE=(4-a)cm
∴阴影部分周长=2+3+(4-a)+a=9cm
故答案为:9
【点睛】
本题考查平移的特点和整式的加减计算,解题关键是利用平移的性质,得出EC=BC-BE.
13.3(答案不唯一)
【解析】
【分析】
先对和进行估算,再根据题意即可得出答案.
【详解】
解:∵<2<3<4<,
∴比大且比小的整数有2,3,4.
故答案为:3(答案不唯一).
【点睛】
此题考查了估算无理数的大小,估算出与是解题的关键.
14.10﹤5x-3≤20
【解析】
【分析】
“的倍与的差”中,被减式为的倍,减式为;大于,且小于或等于,应表示为相减得到的相关式子,相减得到的相关式子.
【详解】
解:的倍与的差大于,且不小于,用不等式组表示.
故答案为:.
【点睛】
本题主要考查列一元一次不等式组,解决本题的关键是理解大于用数学符号表示为“”;不大于用数学符号表示为“”.
15.
【解析】
【分析】
根据、去绝对值运算和零指数幂运算分别求解即可.
【详解】
解:
.
【点睛】
本题考查实数的混合运算,涉及到、去绝对值运算和零指数幂运算,熟练掌握相关运算法则是解决问题的关键.
16.
【解析】
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
【详解】
原式,
当时,原式.
【点睛】
此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
17.(1),数轴表示见解析;(2)-2<x≤3,数轴表示见解析
【解析】
【分析】
(1)先求出不等式的解集,再在数轴上表示出来即可;
(2)先求出不等式组的解集,再在数轴上表示出来即可.
【详解】
解:(1)移项得:,
合并同类项得:,
系数化为1得:,
在数轴上表示为:
(2),
解不等式①得:x≤3,
解不等式②得:x>-2,
所以不等式组的解集是:-2<x≤3,
在数轴上表示为:
【点睛】
本题考查了解一元一次不等式,解一元一次不等式组,在数轴上表示不等式或不等式组的解集等知识点,能求出不等式或不等式组的解集是解此题的关键.
18.(1)见解析(2)B′(﹣1,﹣1),C′(﹣2,1).
【解析】
【详解】
试题分析:(1)根据图形平移的性质画出△A′B′C′即可;
(2)根据点B′和C′在坐标系中的位置写出两点坐标即可.
解:(1)如图所示;
(2)由图可知B′(﹣1,﹣1),C′(﹣2,1).
【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.
19.(1)x7-1;(2)xn+1-1;(3).
【解析】
【分析】
(1)仿照已知等式写出答案即可;
(2)先归纳总结出规律,然后按规律解答即可;
(3)先利用得出规律的变形,然后利用规律解答即可.
【详解】
解:(1)根据题意得:(x-1)(x6+x5+x4+x3+x2+x+1)=x7-1;
(2)根据题意得:(x-1)(x"+x"-1+.…+x+1)=x"+1-1;
(3)原式=×(3-1)(1+3+32+···+349+350)= ×(x50+1-1)=
故答案为:(1)x7-1;(2)xn+1-1;(3).
【点睛】
本题考查了平方差公式以及规律型问题,弄清题意、发现数字的变化规律是解答本题的关键.
20.(1)工厂每天应安排24名工人生产A型零件,每天能生产36套产品
(2)①;②至少需要补充60名新工人才能在规定期限完成生产任务
【解析】
【分析】
(1)设工厂每天安排名工人生产A型零件,则工厂每天安排名工人生产B型零件,根据“每套产品由4个A型零件和3个B型零件配套组成”列方程求解即可;
(2)①根据“x名熟练工人和m名新工人生产的A型零件等于1200套产品的A型零件总数”可列方程,进行整理即可;
②设需要补充m名新工人才能在规定期限完成生产任务,安排n名熟练工人生产A型零件,则安排名熟练工人生产B型零件,根据题意,可得关于m、n的方程组,求解即可.
(1)
解:设工厂每天安排名工人生产A型零件,则工厂每天安排名工人生产B型零件,
由题意得:,
解得,
(套)
所以,工厂每天应安排24名工人生产A型零件,每天能生产36套产品.
(2)
①设每天安排x名熟练工人和m名新工人生产A型零件,则安排名熟练工人生产B型零件,
由题意得,,
整理得;
②设需要补充m名新工人才能在规定期限完成生产任务,安排n名熟练工人生产A型零件,则安排名熟练工人生产B型零件,
由题意得,
解得,
所以,至少需要补充60名新工人才能在规定期限完成生产任务.
【点睛】
本题考查了一元一次方程的实际应用,二元一次方程组的实际应用,准确理解题意,熟练掌握知识点是解题的关键.
21.(1)
(2)1,2,3,图见解析
(3)
【解析】
【分析】
(1)用两种方法表示出来面积即可得出等式;
(2)先计算多项式乘以多项式,即可得出需要纸板的数量,然后根据纸板数量画出相应图形即可;
(3)设,,利用(1)中结论进行变形求解即可.
(1)
解:根据图形可得:,
故答案为:
(2)
解:(a+b)(a+2b)=,
需要A硬纸板1张,B硬纸板2张,C硬纸板3张,
故答案为:1,2,3;
设计图可以为:
a ab ab ab ab
b a ab
ab
a b b a b b
(3)
设,
由题意得:,
由(1)知:
∴
即.
【点睛】
本题主要考查多项式乘法与图形面积的关系,熟练掌握多项式乘以多项式的计算方法及面积表示方法是解题关键.
22.(1)β-α;(2)∠ATC=-∠B+60°;(3)∠B=(β-α)
【解析】
【分析】
(1)利用平行线的性质和三角形外角的性质求解即可;
(2)过T作TK∥MN,根据平行线的性质得出∠ATK=∠MAT,∠KTC=∠TCE,再由∠MAT=∠BAN,∠TCB=2∠TCE,表示出∠ATC=-(β-α)+60°,结合∠B=β-α,即可求出结果;
(3)根据题中条件可得:∠BAH=(180°-α),∠BCA=(180°-β),结合∠BAH=∠B+∠BCA,可得∠B.
【详解】
解:(1)如图,设MN与BC交于点G,
∵MN∥EF,
∴∠BGN=∠BCF=β,
∴∠B=∠BGN-∠BAN=β-α,
故答案为:β-α;
(2)如图,过T作TK∥MN,
∵MN∥EF,
∴∠ATK=∠MAT,∠KTC=∠TCE,
∵∠MAT=∠BAN,∠TCB=2∠TCE,
∴∠ATC=∠ATK+∠KTC
=∠MAT+∠TCE
=∠BAN+∠TCB
=α+××(180°-∠BCF)
=α-β+60°
=-(β-α)+60°
∵∠B=β-α,
∴∠ATC=-∠B+60°;
(3)如图,
∵直线AC平分∠MAB,且平分∠ECB,
∴∠BAH=∠MAH=(180°-∠BAN)=(180°-α),
∠BCA=∠ECA=(180°-∠BCF)=(180°-β),
∵∠BAH=∠B+∠BCA,
∴(180°-α)=∠B+(180°-β),
∴∠B=(β-α).
【点睛】
本题综合考查了平行线的性质和三角形外角的性质,以及角平分线的定义,作出适当的辅助线,结合图形进行推理计算是解题的关键.
23.(1) 105°;(2) 135°; (3)5或17;11或23
【解析】
【分析】
(1)根据三角形的内角和定理列式计算即可得解;
(2)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(3)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
【详解】
解:(1)在△CEN中,
∠CEN=180°-∠DCN-∠MNO=180°-45°-30°=105°
(2)∵∠BON=∠N=30°,
∴MN∥CB,
∴∠CEN=180°-∠DCO=180°-45°=135°
(3)如图1,CD在AB上方时,设OM与CD相交于F,
∵CD∥MN,
∴∠OFD=∠M=60°,
在△ODF中,∠MOD=180°-∠D-∠OFD,
=180°-45°-60°,
=75°,
∴旋转角为75°,
t=75°÷15°=5秒;
CD在AB的下方时,设直线OM与CD相交于F,
∵CD∥MN,
∴∠DFO=∠M=60°,
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转角为75°+180°=255°,
t=255°÷15°=17秒;
综上所述,第5或17秒时,边CD恰好与边MN平行;
如图2,CD在OM的右边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGC=90°-∠MNO=90°-30°=60°,
∴∠CON=∠NGC-∠OCD=60°-45°=15°,
∴旋转角为180°-∠CON=180°-15°=165°,
t=165°÷15°=11秒,
CD在OM的左边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGD=90°-∠MNO=90°-30°=60°,
∴∠AOC=∠NGD-∠C=60°-45°=15°,
∴旋转角为360°-∠AOC=360°-15°=345°,
t=345°÷15°=23秒,
综上所述,第11或23秒时,直线CD恰好与直线MN垂直.
【点睛】
本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,难点在于(3)分情况讨论,作出图形更形象直观.
同课章节目录
