2.1.2指数函数及其性质【第一课时】
文档属性
| 名称 | 2.1.2指数函数及其性质【第一课时】 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-25 00:00:00 | ||
图片预览








文档简介
课件32张PPT。2.1.2指数函数及其性质高中数学新课标人教A版必修①第一课时 在印度有一个古老的传说:舍罕王
打算奖赏国际象棋的发明人--宰相
西萨·班·达依尔。国王问他想要什么,
他对国王说:"陛下,请您在这棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!"国王觉得这要求太容易满足了,命令给他这些麦粒。当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求。棋盘上的麦粒总数为:=18446744073709551615(粒) ,1000粒约40克
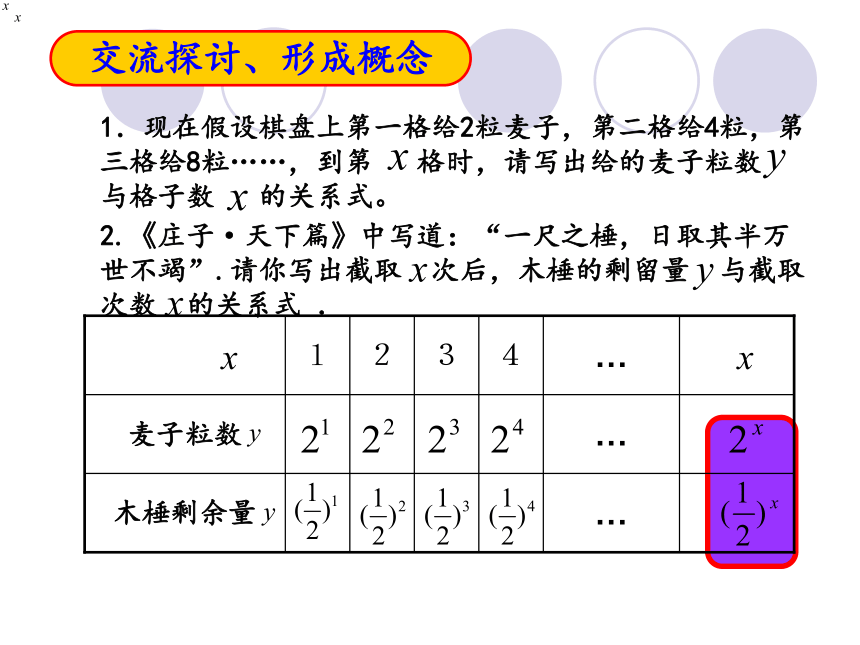
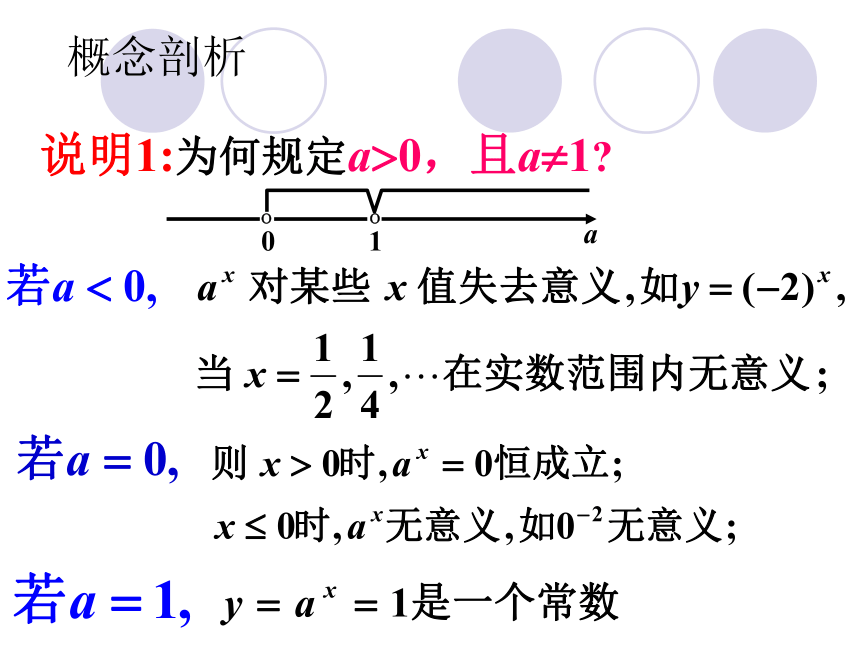
麦粒有7000多亿吨(现每年全球的小麦总量约6.5亿吨)《庄子 天下篇》庄 子2.《庄子·天下篇》中写道:“一尺之棰,日取其半万世不竭”.请你写出截取 次后,木棰的剩留量 与截取次数 的关系式 .1.现在假设棋盘上第一格给2粒麦子,第二格给4粒,第三格给8粒……,到第 格时,请写出给的麦子粒数 与格子数 的关系式。交流探讨、形成概念 提炼 我们把这种自变量在指数位置上而底数是一个大于0且不等于1的常量的函数叫做指数函数.概念剖析说明1:为何规定a?0,且a?1?指数函数的特征:
【提示】依据指数函数y=ax(a>0且a≠1)解析式的结构特征:
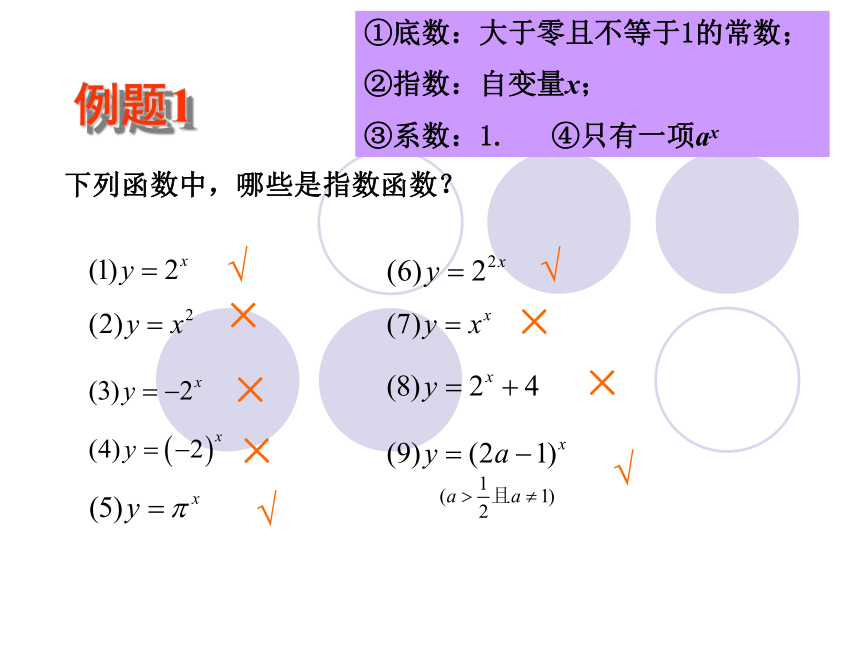
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1;
④只有一项ax .说明2下列函数中,哪些是指数函数? √√例题1√√×××××①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1. ④只有一项ax2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.∴ a = 2D探求新知、深化理解特殊点
定义域探求新知、深化理解设问2:已知函数的解析式,怎么得到函 数的图象,一般用什么方法?列表、描点、连线作图在同一直角坐标系画出 ,
的图象。
并观察:两个函数的图象有什么关系?观察:两个函数的图象有什么关系?y=2x 两个函数图像关于y轴对称比较图象 得出特征(0,1)a >10 < a < 1(-∞,+∞)(左右无限延伸)(0,+∞)(在x轴上方)即x = 0时,y = 1都过(0,1)点增函数(自左向右上升)减函数(自左向右下降)x>0时,y>1x>0时, 01(y轴左侧,在直线y=1的上方)图象定义域值域定点单调性函数值的变化范围(y轴右侧,在直线y=1上方)比较图象 得出特征探究1:不同底数的指数函数图象有什么特点?比较图象 得出特征当指数函数底数大于1时,图象上升,且底数越大时图象向上越靠近于y轴;当底数大于0小于1时,图象下降,底数越小图象向右越靠近于x轴.0性
质 011.定义域为R,值域为(0,+?).2.过定点(0,1)即x=0时,y=13.在R上是增函数3.在R上是减函数4.当x>0时,y>1;当x<0时,00时, 01.5.既不是奇函数也不是偶函数.图 象 (0,1)y=1(1)考察指数函数y=1.5x .
由于底数1.5>1 ,所以指数函数
y=1.5x 在R上是增函数.解:∵2.5<3.2 ∴1.52.5<1.53.2(2)指数函数y=0.5x 在R上是减函数.∵-1.2>-1.5 ∴0.5-1.2<0.5-1.5(1)指数函数y=1.5x 在R上是增函数. 变式一>< 法一: 图象法法二: 作商法 (两个指数式的商与1比较)练习:<<指数相同,底数不同 分析:= 1 =>>>><底数不同,指数不同(4)
②异底同指:构造函数法(多个),利用函数图象在y轴左右两侧的特点。比较指数幂大小的方法:①同底异指:构造函数法(一个), 利用函数的单调性,若底数是参变量要注意分类讨论。③异底异指:寻求中间量1.指数函数的图象和性质例3.求下列函数的定义域、值域: 函数的定义域为{x|x ? 0}, 值域为{y |y>0 ,且y?1}.解 (1)(2) 函数的定义域为
性
质 011.定义域为R,值域为(0,+?).2.过定点(0,1)即x=0时,y=13.在R上是增函数3.在R上是减函数4.当x>0时,y>1;当x<0时,00时, 01.5.既不是奇函数也不是偶函数.图 象 (0,1)y=12.指数函数的图象和性质练习:y=ax(a>0且 a≠1)图象必过
点_______2 y=ax-2(a>0且 a≠1)图象必
过点_______y=ax+3-1(a>0且 a≠1)图象
必过点________(0,1)(2,1)(-3,0)
性
质 011.定义域为R,值域为(0,+?).2.过定点(0,1)即x=0时,y=13.在R上是增函数3.在R上是减函数4.当x>0时,y>1;当x<0时,00时, 01.5.既不是奇函数也不是偶函数.图 象 (0,1)y=1求定点,先令指数为0,再计算x,y的值 已知指数函数
的图像经过点 求 的值.例4待定系数法求a例5:实际应用
截止到1999年底,我国人口约13亿。如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?
13 13(1+1%)13(1+1%)213(1+1%)3 13(1+1%)ⅹ当x=20时,y=13×1.0120 ≈16(亿).解:设今后人口年平均增长率为1℅,经过x年后,我国人口数为y亿.1999年底,我国人口约为13亿;经过1年(即2000年),人口
数为
13+13 × 1℅= 13×(1+1℅)(亿);经过2年(即2001年),人口数为
13×(1+1℅)+ 13×(1+1℅)× 1℅
= 13×(1+1℅)2 (亿);经过3年(即2002年),人口数为
13×(1+1℅)2+ 13×(1+1℅)2× 1℅
= 13×(1+1℅)3 (亿);
……
所以,经过x年后,人口数为
y= 13×(1+1℅)x=13×1.01x(亿).所以,经过20年后,我国人口数最多为16亿。(1)如果人口年均增长率提高1个百分点,利
用计算器分别计算20年,33年后我国的人口数.探 究⑴ y=13×(1+2℅)x=13×1.02 xy20≈19(亿),y33≈25(亿)(2)如果年均增长率保持在2%,利用计算器 计算2020~2100年,每隔5年相应的人口数.⑵ 2020 20, 2025 ,
2030 , 2035 ,
…… 2100 . 22242796(3)你看到我国人口数的增长呈现什么趋势?(4)你是如何看待我国的计划生育政策的?习题2.1B组题3
课堂小结1.指数函数的概念2.指数函数的图像和性质3.指数函数性质的简单应用 数形结合,由具体到一般1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数3.在R上是减函数4.非奇非偶函数
x函 数 图 象1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
y0 a>1函数性质思想与方法:y=1(0,1)x在第一象限内,按逆时针方向旋转,底数a越来越大0
打算奖赏国际象棋的发明人--宰相
西萨·班·达依尔。国王问他想要什么,
他对国王说:"陛下,请您在这棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!"国王觉得这要求太容易满足了,命令给他这些麦粒。当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求。棋盘上的麦粒总数为:=18446744073709551615(粒) ,1000粒约40克
麦粒有7000多亿吨(现每年全球的小麦总量约6.5亿吨)《庄子 天下篇》庄 子2.《庄子·天下篇》中写道:“一尺之棰,日取其半万世不竭”.请你写出截取 次后,木棰的剩留量 与截取次数 的关系式 .1.现在假设棋盘上第一格给2粒麦子,第二格给4粒,第三格给8粒……,到第 格时,请写出给的麦子粒数 与格子数 的关系式。交流探讨、形成概念 提炼 我们把这种自变量在指数位置上而底数是一个大于0且不等于1的常量的函数叫做指数函数.概念剖析说明1:为何规定a?0,且a?1?指数函数的特征:
【提示】依据指数函数y=ax(a>0且a≠1)解析式的结构特征:
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1;
④只有一项ax .说明2下列函数中,哪些是指数函数? √√例题1√√×××××①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1. ④只有一项ax2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.∴ a = 2D探求新知、深化理解特殊点
定义域探求新知、深化理解设问2:已知函数的解析式,怎么得到函 数的图象,一般用什么方法?列表、描点、连线作图在同一直角坐标系画出 ,
的图象。
并观察:两个函数的图象有什么关系?观察:两个函数的图象有什么关系?y=2x 两个函数图像关于y轴对称比较图象 得出特征(0,1)a >10 < a < 1(-∞,+∞)(左右无限延伸)(0,+∞)(在x轴上方)即x = 0时,y = 1都过(0,1)点增函数(自左向右上升)减函数(自左向右下降)x>0时,y>1x>0时, 0
质 0
由于底数1.5>1 ,所以指数函数
y=1.5x 在R上是增函数.解:∵2.5<3.2 ∴1.52.5<1.53.2(2)指数函数y=0.5x 在R上是减函数.∵-1.2>-1.5 ∴0.5-1.2<0.5-1.5(1)指数函数y=1.5x 在R上是增函数. 变式一>< 法一: 图象法法二: 作商法 (两个指数式的商与1比较)练习:<<指数相同,底数不同 分析:= 1 =>>>><底数不同,指数不同(4)
②异底同指:构造函数法(多个),利用函数图象在y轴左右两侧的特点。比较指数幂大小的方法:①同底异指:构造函数法(一个), 利用函数的单调性,若底数是参变量要注意分类讨论。③异底异指:寻求中间量1.指数函数的图象和性质例3.求下列函数的定义域、值域: 函数的定义域为{x|x ? 0}, 值域为{y |y>0 ,且y?1}.解 (1)(2) 函数的定义域为
性
质 0
点_______2 y=ax-2(a>0且 a≠1)图象必
过点_______y=ax+3-1(a>0且 a≠1)图象
必过点________(0,1)(2,1)(-3,0)
性
质 0
13 13(1+1%)13(1+1%)213(1+1%)3 13(1+1%)ⅹ当x=20时,y=13×1.0120 ≈16(亿).解:设今后人口年平均增长率为1℅,经过x年后,我国人口数为y亿.1999年底,我国人口约为13亿;经过1年(即2000年),人口
数为
13+13 × 1℅= 13×(1+1℅)(亿);经过2年(即2001年),人口数为
13×(1+1℅)+ 13×(1+1℅)× 1℅
= 13×(1+1℅)2 (亿);经过3年(即2002年),人口数为
13×(1+1℅)2+ 13×(1+1℅)2× 1℅
= 13×(1+1℅)3 (亿);
……
所以,经过x年后,人口数为
y= 13×(1+1℅)x=13×1.01x(亿).所以,经过20年后,我国人口数最多为16亿。(1)如果人口年均增长率提高1个百分点,利
用计算器分别计算20年,33年后我国的人口数.探 究⑴ y=13×(1+2℅)x=13×1.02 xy20≈19(亿),y33≈25(亿)(2)如果年均增长率保持在2%,利用计算器 计算2020~2100年,每隔5年相应的人口数.⑵ 2020 20, 2025 ,
2030 , 2035 ,
…… 2100 . 22242796(3)你看到我国人口数的增长呈现什么趋势?(4)你是如何看待我国的计划生育政策的?习题2.1B组题3
课堂小结1.指数函数的概念2.指数函数的图像和性质3.指数函数性质的简单应用 数形结合,由具体到一般1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数3.在R上是减函数4.非奇非偶函数
x函 数 图 象1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
1.定义域为R,值域为(0,+?).2.当x=0时,y=13.在R上是增函数4.非奇非偶函数
y0 a>1函数性质思想与方法:y=1(0,1)x在第一象限内,按逆时针方向旋转,底数a越来越大0
