2022-2023学年北师大版九年级数学上册4.5相似三角形判定定理的证明 选择专项练习题(含解析)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册4.5相似三角形判定定理的证明 选择专项练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 312.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 00:00:00 | ||
图片预览


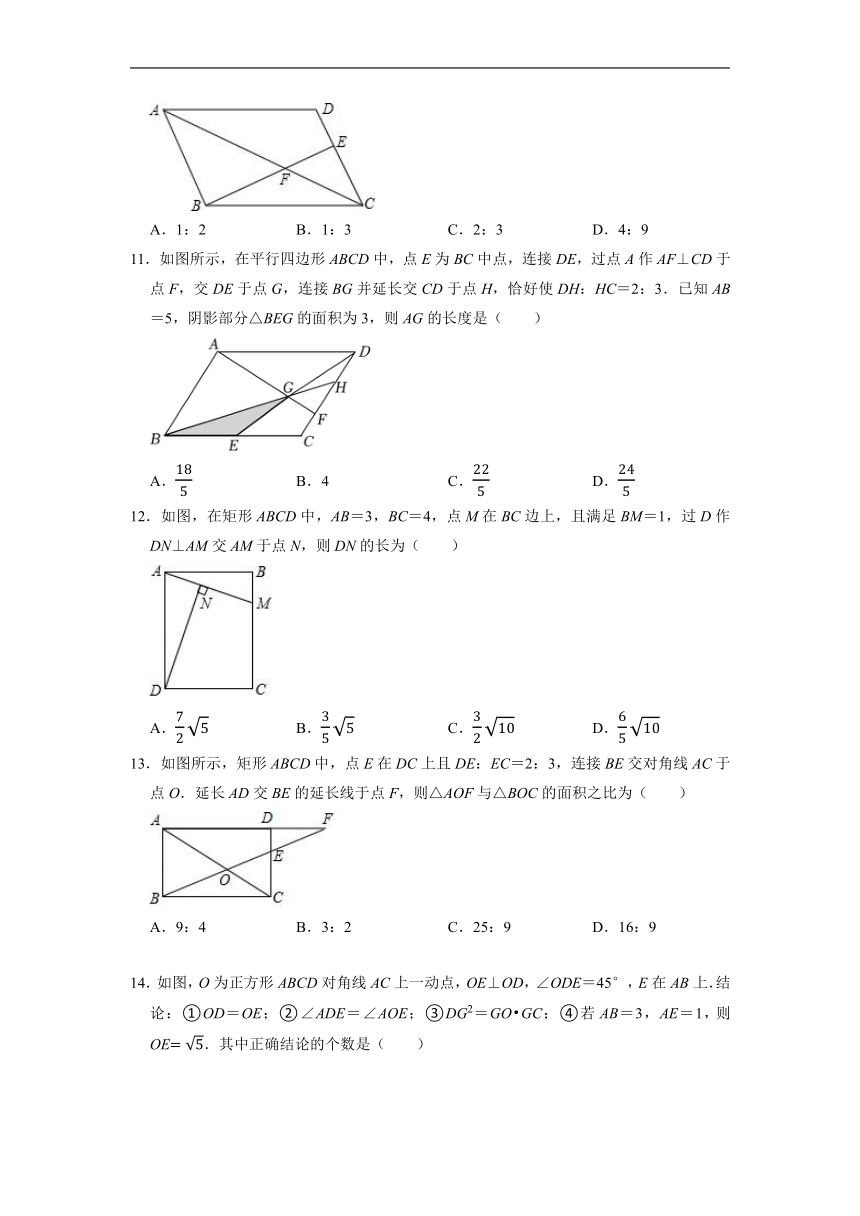
文档简介
2022-2023学年北师大版九年级数学上册《4.5相似三角形判定定理的证明》
选择专项练习题(附答案)
1.如图,△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
2.图中所示的△ABC中,E、F分别在边AB、AC上,EF∥BC,AB=3,AE=2,EF=4,则BC=( )
A.6 B.12 C.18 D.24
3.已知:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.3:2 C.4:9 D.9:4
4.如图,在△ABC中,D、E分别是边AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
5.如图,已知点D、E是△ABC中AB边上的点,△CDE是等边三角形,∠ACB=120°,则下列结论中错误的是( )
A.AC2=AD AB B.BC2=BE AB
C.DE2=AD BE D.AC BC=AE BD
6.如图,在△ABC中,AB=6,BC=5,点D、E分别在BC、AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是( )
A.2 B.3 C.4 D.5
7.如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
A.3:2 B.3:1 C.1:1 D.1:2
8.如图,△ABC中,∠ABD=∠C,若AB=4,AD=2,则CD边的长是( )
A.2 B.4 C.6 D.8
9.如图,在Rt△ABC中,∠C=90°,放置边长分别为3,4,x的三个正方形,则x的值为( )
A.12 B.7 C.6 D.5
10.如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
A.1:2 B.1:3 C.2:3 D.4:9
11.如图所示,在平行四边形ABCD中,点E为BC中点,连接DE,过点A作AF⊥CD于点F,交DE于点G,连接BG并延长交CD于点H,恰好使DH:HC=2:3.已知AB=5,阴影部分△BEG的面积为3,则AG的长度是( )
A. B.4 C. D.
12.如图,在矩形ABCD中,AB=3,BC=4,点M在BC边上,且满足BM=1,过D作DN⊥AM交AM于点N,则DN的长为( )
A. B. C. D.
13.如图所示,矩形ABCD中,点E在DC上且DE:EC=2:3,连接BE交对角线AC于点O.延长AD交BE的延长线于点F,则△AOF与△BOC的面积之比为( )
A.9:4 B.3:2 C.25:9 D.16:9
14.如图,O为正方形ABCD对角线AC上一动点,OE⊥OD,∠ODE=45°,E在AB上.结论:①OD=OE;②∠ADE=∠AOE;③DG2=GO GC;④若AB=3,AE=1,则OE.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
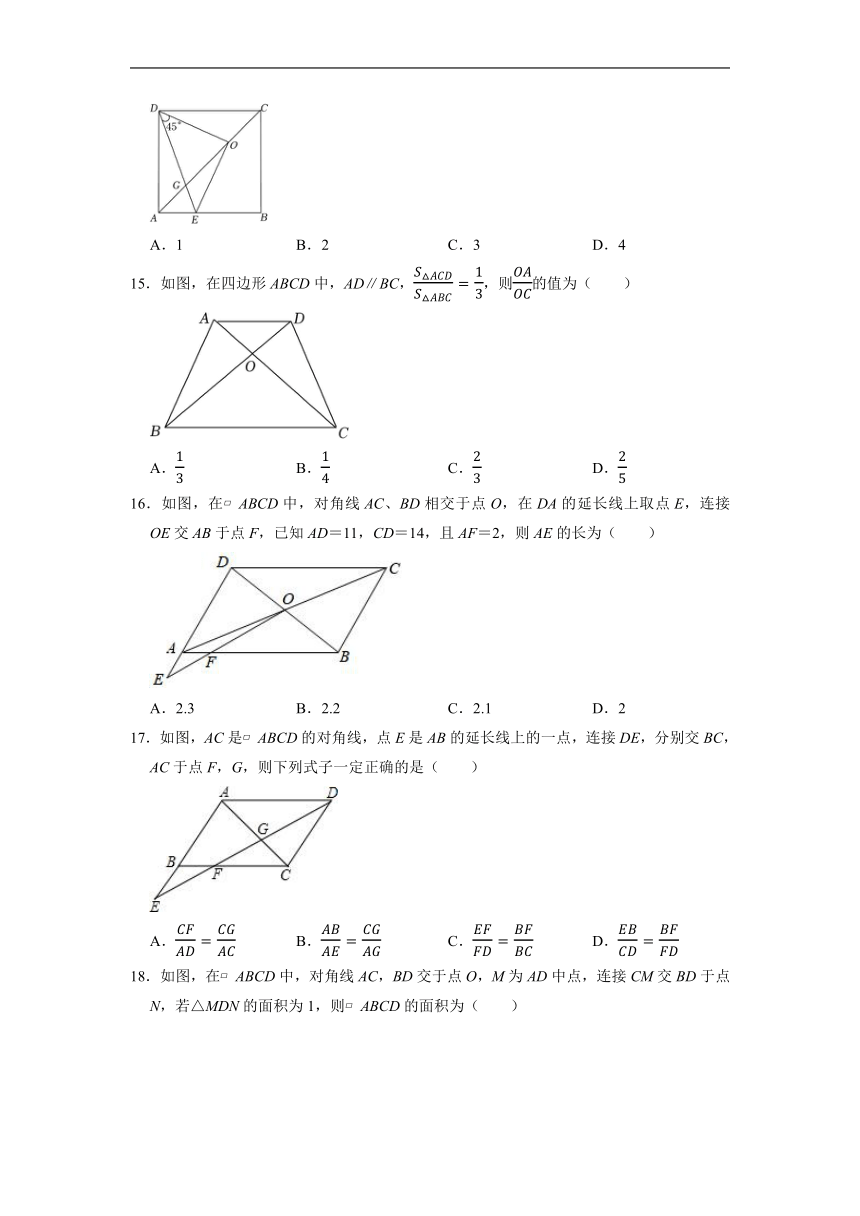
15.如图,在四边形ABCD中,AD∥BC,,则的值为( )
A. B. C. D.
16.如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
17.如图,AC是 ABCD的对角线,点E是AB的延长线上的一点,连接DE,分别交BC,AC于点F,G,则下列式子一定正确的是( )
A. B. C. D.
18.如图,在 ABCD中,对角线AC,BD交于点O,M为AD中点,连接CM交BD于点N,若△MDN的面积为1,则 ABCD的面积为( )
A.12 B.14 C.15 D.20
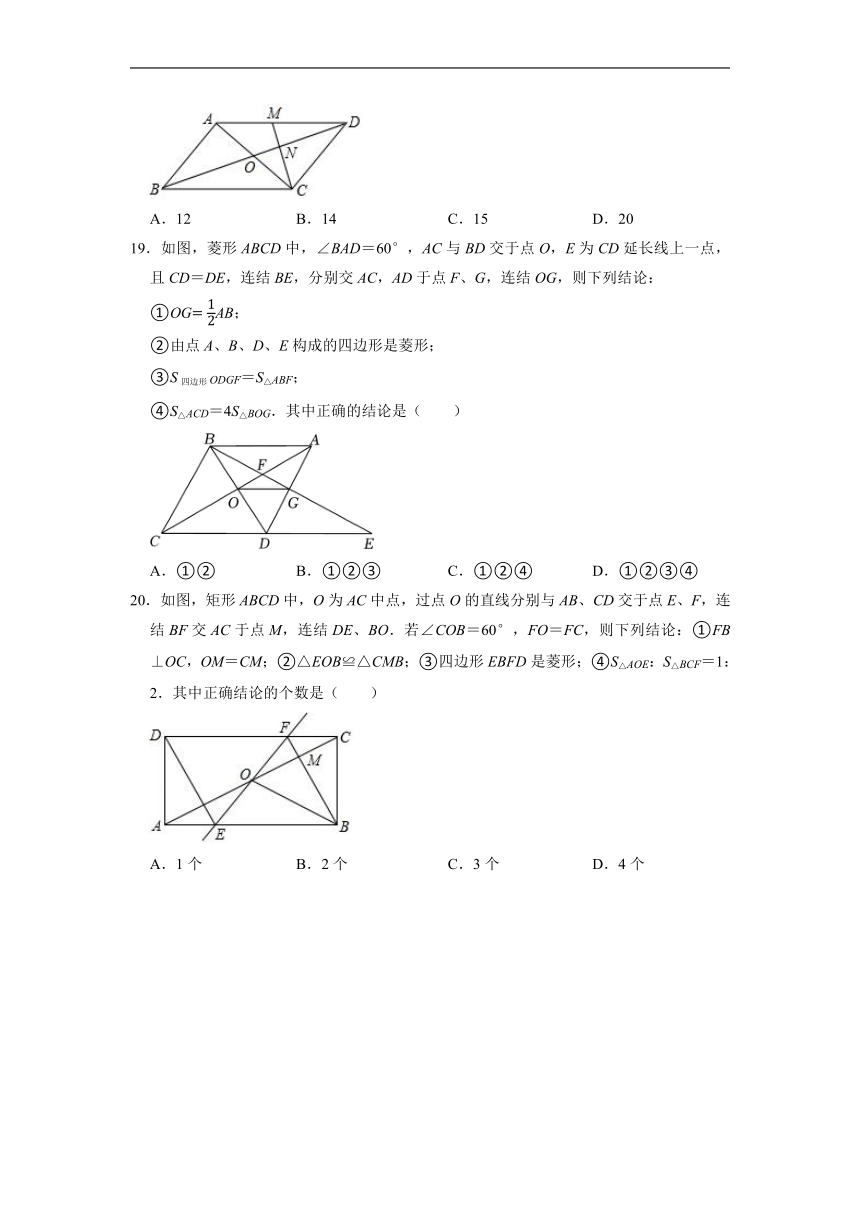
19.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:
①OGAB;
②由点A、B、D、E构成的四边形是菱形;
③S四边形ODGF=S△ABF;
④S△ACD=4S△BOG.其中正确的结论是( )
A.①② B.①②③ C.①②④ D.①②③④
20.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④S△AOE:S△BCF=1:2.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
参考答案
1.解:∵DE∥BC,EF∥AB,
∴△ADE∽△ABC,△EFC∽△ABC,四边形BDEF为平行四边形,
∴△ADE∽△EFC,DE=BF,
∴.
故选:D.
2.解:∵EF∥AB,
∴△AEF∽△ABC,
∴,
∵AB=3,AE=2,EF=4,
∴,
解得,BC=6,
故选:A.
3.解:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,
∴△AOB∽△DOC,且AO:OD=2:3,
∴S△AOB:S△DOC=AO2:OD2=4:9.
故选:C.
4. 解:∵S△BDE:S△CDE=1:3,
∴BE:EC=1:3;
∴BE:BC=1:4;
∵DE∥AC,
∴△DOE∽△AOC,
∴,
∴,故选:D.
5.解:如图所示:
∵△CDE是等边三角形,
∴∠CDE=60°,
又∵∠ADC+∠CDE=180°,
∴∠ADC=120°,
又∵∠ACB=120°,
∴∠ADC=∠ACB,
在△ADC和△ACB中,
,
∴△ADC∽△ACB(AA),
∴,
∴AC2=AB AD,
即答案A正确;
同理可证:△CEB∽△ACB(AA),
∴,
∴BC2=AB BE,
即答案B正确;
∵∠ACD=∠B,∠ADC=∠CEB=120°,
∴△ACD∽△CBE(AA),
∴,
∴CD CE=AD BE,
又∵CD=DE=EC,
∴DE2=AD BE,
即答案C正确;
∵△ACE与△BDC不相似,
∴AC BC=AE BD不成立,
即答案D错误.
故选:D.
6.解:连接DE,过点D作DH⊥AB于H,如图所示:
∵CD=2BD,CE=2AE,
∴2,
∴DE∥AB,
∴△CDE∽△CBA,△DEF∽△ABF,
∴,,
∴,
∵DE∥AB,
∴S△ABE=S△ABD,
∴S△AEF=S△BDF,
∴S△AEFS△ABD,
∵BDBC,
∵AB=6一定,当DH最大时,△ABD的面积最大,
∵DH≤BD,
∴DH=BD时,DH最大,
即当AB⊥BD时,△ABD的面积最大,最大值6=5,
∴△AEF的面积的最大值5=2,
故选:A.
7.解:∵ ABCD,故AD∥BC,
∴△DEF∽△BCF,
∴,
∵点E是边AD的中点,
∴AE=DEAD,
∴.
故选:D.
8.解:∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴,AC=AD+DC,
∴,
∴DC=6.
答:DC边的长为6.
故选:C.
9.解:∵在Rt△ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,
∴△CEF∽△OME∽△PFN,
∴OE:PN=OM:PF,
∵EF=x,MO=3,PN=4,
∴OE=x﹣3,PF=x﹣4,
∴(x﹣3):4=3:(x﹣4),
∴(x﹣3)(x﹣4)=12,即x2﹣4x﹣3x+12=12,
∴x=0(不符合题意,舍去)或x=7.
故选:B.
10.解:∵四边形ABCD是平行四边形,
∴DC∥AB,CD=AB.
∴△DFE∽△BFA,
∵DE:EC=1:2,
∴EC:DC=CE:AB=2:3,
∴C△CEF:C△ABF=2:3.
故选:C.
11.解:延长DE与AB的延长线交于点M,连接CG,如图,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠M=∠EDC,
∵BE=CE,∠BEM=∠CED,
∴△BEM≌△CED(AAS),
∴EM=ED,BM=CD,
∵DH:HC=2:3,
∴DH:CD=2:5,
∴DH:BM=2:5,
∵DH∥BM,
∴△DHG∽△MBG,
∴,
∴,
∵DE=ME,
∴,
∴,
∵△BEG的面积为3,点E为BC中点,
∴S△CEG=S△BEG=3,
∴S△CDG=4,
∵CD=AB=5,
∴,
∴FG,
∵HF∥AB,
∴△HFG∽△BAG,
∴,
∴AGFG=4.
故选:B.
12.解:连接DM,如图所示:
∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=4,△AMD底边AD上的高为AB,
AM,
∵△ADM的面积AM×DNAD×AB,
∴DN;
故选:D.
13.解:
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴△AOB∽△COE,
∵DE:EC=2:3,
∴CE:CD=3:5,
∴CE:CD=CE:AB=3:5,
∴S△AOF:S△BOC=25:9.
故选:C.
14.解:∵OE⊥OD,
∴∠DOE=90°,
∵∠ODE=45°,
∴△DOE是等腰直角三角形,
∴OD=OE,
∴①正确;
∵四边形ABCD是正方形,
∴∠DAC=∠BAC,
∵∠DEO=90°﹣∠ODE=45°,
∴∠DAC=∠DEO=45°,
∵∠AGD=∠EGO,
∠DAC+∠AGD+∠ADE=180°,
∠DEO+∠EGO+∠AOE=180°,
∴∠ADE=∠AOE,
∴②正确;
∵四边形ABCD是正方形,
∴∠ACD=∠ACB,
∵∠ODE=45°,
∴∠ODE=∠ACD=45°,
∵∠DGO=∠DGC,
∴△GOD∽△GDC,
∴,
∴DG2=GO GC;
∴③正确;
∵四边形ABCD是正方形,AB=3,AE=1,
∴AD=CD=AB=3,
∴DE,
∵△DOE是等腰直角三角形,
∴OE=OD,
∴④正确,
∴正确结论个数为4,
故选:D.
15.解:∵AD∥BC,
∴设AD与BC之间的距离为h,
∴,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
∴△ADO∽△CBO,
∴,
故选:A.
16.解:过O点作OM∥CD,
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD=14,
∴OM是△ABD的中位线,
∴AM=DMAD,OMBA=7,
∵AF∥OM,
∴△AEF∽△MEO,
∴,
∴,
∴AE2.2,
故选:B.
17.解:∵四边形ABCD 是平行四边形,
∴AD∥BC,AB=CD,CD∥AB,
∴△CFG∽△ADG,
∴,
故A不正确;
∵CD∥AE,
∴△CDG∽△AEG,
∴,
∵AB=DC,
∴,
故B正确;
∵△BEF∽△CDF,
∴,
故C,D不正确;
故选:B.
18.解:∵平行四边形ABCD,
∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴,
∵M为AD中点,
∴,
∴BN=2DN,
∴,,
∵△MDN的面积为1,
∴S△CNB=4,S△CND=2,
∴S△BCD=S△CNB+S△CND=4+2=6,
∴S平行四边形ABCD=2S△BCD=2×6=12.
故选:A.
19.解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ABD的中位线,
∴OGAB,故①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴平行四边形ABDE是菱形,故②正确;
∵OA=OC,AG=DG,
∴OG是△ACD的中位线,
∴OG∥CD∥AB,OGCD,
∴S△ACD=4S△AOG,
∵S△AOG=S△BOG,
∴S△ACD=4S△BOG,故④正确;
连接FD,如图:
∵△ABD是等边三角形,AO平分∠BAD,BG平分∠ABD,
∴F到△ABD三边的距离相等,
∴S△BDF=S△ABF=2S△BOF=2S△DOF=S四边形ODGF,
∴S四边形ODGF=S△ABF,故③正确;
正确的是①②③④,
故选:D.
20.解:连接OD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中,
,
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM,
∴①正确;
∵四边形EBFD是菱形,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
由四边形EBFD是菱形,得:△EOB≌△FOB,
由①可知BF是OC的垂直平分线,则有△FOB≌△FCB,
∴△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误;
④∵四边形ABCD是矩形,四边形EBFD是菱形,
∴OA=OC,∠COF=∠AOE,OF=OE,
∴△AOE≌△COF(SAS),
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∵∠FCO=30°,
∴FMCM,BMCM,
∴,
∴S△FOM:S△BOF=1:4,
∵∠OGE=∠OMF,∠GOE=∠MOF,OE=OF,
∴△GEO≌△MFO(AAS),
∴S△GEO=S△MFO,
∴S△DEF=S△EFB=2S△BOF,
设S△EGO=x,则S△AOE=2x,S△BOF=4x,
S四边形DGOF=S△DEF﹣S△EGO=S△EFB﹣S△EGO=8x﹣x,
∴S△AOE:S四边形DGOF=2x:(8x﹣x)=2:7,
故④正确;
所以其中正确结论的个数为3个,
故选:C.
选择专项练习题(附答案)
1.如图,△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
2.图中所示的△ABC中,E、F分别在边AB、AC上,EF∥BC,AB=3,AE=2,EF=4,则BC=( )
A.6 B.12 C.18 D.24
3.已知:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.3:2 C.4:9 D.9:4
4.如图,在△ABC中,D、E分别是边AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
5.如图,已知点D、E是△ABC中AB边上的点,△CDE是等边三角形,∠ACB=120°,则下列结论中错误的是( )
A.AC2=AD AB B.BC2=BE AB
C.DE2=AD BE D.AC BC=AE BD
6.如图,在△ABC中,AB=6,BC=5,点D、E分别在BC、AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是( )
A.2 B.3 C.4 D.5
7.如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
A.3:2 B.3:1 C.1:1 D.1:2
8.如图,△ABC中,∠ABD=∠C,若AB=4,AD=2,则CD边的长是( )
A.2 B.4 C.6 D.8
9.如图,在Rt△ABC中,∠C=90°,放置边长分别为3,4,x的三个正方形,则x的值为( )
A.12 B.7 C.6 D.5
10.如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
A.1:2 B.1:3 C.2:3 D.4:9
11.如图所示,在平行四边形ABCD中,点E为BC中点,连接DE,过点A作AF⊥CD于点F,交DE于点G,连接BG并延长交CD于点H,恰好使DH:HC=2:3.已知AB=5,阴影部分△BEG的面积为3,则AG的长度是( )
A. B.4 C. D.
12.如图,在矩形ABCD中,AB=3,BC=4,点M在BC边上,且满足BM=1,过D作DN⊥AM交AM于点N,则DN的长为( )
A. B. C. D.
13.如图所示,矩形ABCD中,点E在DC上且DE:EC=2:3,连接BE交对角线AC于点O.延长AD交BE的延长线于点F,则△AOF与△BOC的面积之比为( )
A.9:4 B.3:2 C.25:9 D.16:9
14.如图,O为正方形ABCD对角线AC上一动点,OE⊥OD,∠ODE=45°,E在AB上.结论:①OD=OE;②∠ADE=∠AOE;③DG2=GO GC;④若AB=3,AE=1,则OE.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
15.如图,在四边形ABCD中,AD∥BC,,则的值为( )
A. B. C. D.
16.如图,在 ABCD中,对角线AC、BD相交于点O,在DA的延长线上取点E,连接OE交AB于点F,已知AD=11,CD=14,且AF=2,则AE的长为( )
A.2.3 B.2.2 C.2.1 D.2
17.如图,AC是 ABCD的对角线,点E是AB的延长线上的一点,连接DE,分别交BC,AC于点F,G,则下列式子一定正确的是( )
A. B. C. D.
18.如图,在 ABCD中,对角线AC,BD交于点O,M为AD中点,连接CM交BD于点N,若△MDN的面积为1,则 ABCD的面积为( )
A.12 B.14 C.15 D.20
19.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:
①OGAB;
②由点A、B、D、E构成的四边形是菱形;
③S四边形ODGF=S△ABF;
④S△ACD=4S△BOG.其中正确的结论是( )
A.①② B.①②③ C.①②④ D.①②③④
20.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④S△AOE:S△BCF=1:2.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
参考答案
1.解:∵DE∥BC,EF∥AB,
∴△ADE∽△ABC,△EFC∽△ABC,四边形BDEF为平行四边形,
∴△ADE∽△EFC,DE=BF,
∴.
故选:D.
2.解:∵EF∥AB,
∴△AEF∽△ABC,
∴,
∵AB=3,AE=2,EF=4,
∴,
解得,BC=6,
故选:A.
3.解:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,
∴△AOB∽△DOC,且AO:OD=2:3,
∴S△AOB:S△DOC=AO2:OD2=4:9.
故选:C.
4. 解:∵S△BDE:S△CDE=1:3,
∴BE:EC=1:3;
∴BE:BC=1:4;
∵DE∥AC,
∴△DOE∽△AOC,
∴,
∴,故选:D.
5.解:如图所示:
∵△CDE是等边三角形,
∴∠CDE=60°,
又∵∠ADC+∠CDE=180°,
∴∠ADC=120°,
又∵∠ACB=120°,
∴∠ADC=∠ACB,
在△ADC和△ACB中,
,
∴△ADC∽△ACB(AA),
∴,
∴AC2=AB AD,
即答案A正确;
同理可证:△CEB∽△ACB(AA),
∴,
∴BC2=AB BE,
即答案B正确;
∵∠ACD=∠B,∠ADC=∠CEB=120°,
∴△ACD∽△CBE(AA),
∴,
∴CD CE=AD BE,
又∵CD=DE=EC,
∴DE2=AD BE,
即答案C正确;
∵△ACE与△BDC不相似,
∴AC BC=AE BD不成立,
即答案D错误.
故选:D.
6.解:连接DE,过点D作DH⊥AB于H,如图所示:
∵CD=2BD,CE=2AE,
∴2,
∴DE∥AB,
∴△CDE∽△CBA,△DEF∽△ABF,
∴,,
∴,
∵DE∥AB,
∴S△ABE=S△ABD,
∴S△AEF=S△BDF,
∴S△AEFS△ABD,
∵BDBC,
∵AB=6一定,当DH最大时,△ABD的面积最大,
∵DH≤BD,
∴DH=BD时,DH最大,
即当AB⊥BD时,△ABD的面积最大,最大值6=5,
∴△AEF的面积的最大值5=2,
故选:A.
7.解:∵ ABCD,故AD∥BC,
∴△DEF∽△BCF,
∴,
∵点E是边AD的中点,
∴AE=DEAD,
∴.
故选:D.
8.解:∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴,AC=AD+DC,
∴,
∴DC=6.
答:DC边的长为6.
故选:C.
9.解:∵在Rt△ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,
∴△CEF∽△OME∽△PFN,
∴OE:PN=OM:PF,
∵EF=x,MO=3,PN=4,
∴OE=x﹣3,PF=x﹣4,
∴(x﹣3):4=3:(x﹣4),
∴(x﹣3)(x﹣4)=12,即x2﹣4x﹣3x+12=12,
∴x=0(不符合题意,舍去)或x=7.
故选:B.
10.解:∵四边形ABCD是平行四边形,
∴DC∥AB,CD=AB.
∴△DFE∽△BFA,
∵DE:EC=1:2,
∴EC:DC=CE:AB=2:3,
∴C△CEF:C△ABF=2:3.
故选:C.
11.解:延长DE与AB的延长线交于点M,连接CG,如图,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠M=∠EDC,
∵BE=CE,∠BEM=∠CED,
∴△BEM≌△CED(AAS),
∴EM=ED,BM=CD,
∵DH:HC=2:3,
∴DH:CD=2:5,
∴DH:BM=2:5,
∵DH∥BM,
∴△DHG∽△MBG,
∴,
∴,
∵DE=ME,
∴,
∴,
∵△BEG的面积为3,点E为BC中点,
∴S△CEG=S△BEG=3,
∴S△CDG=4,
∵CD=AB=5,
∴,
∴FG,
∵HF∥AB,
∴△HFG∽△BAG,
∴,
∴AGFG=4.
故选:B.
12.解:连接DM,如图所示:
∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=4,△AMD底边AD上的高为AB,
AM,
∵△ADM的面积AM×DNAD×AB,
∴DN;
故选:D.
13.解:
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴△AOB∽△COE,
∵DE:EC=2:3,
∴CE:CD=3:5,
∴CE:CD=CE:AB=3:5,
∴S△AOF:S△BOC=25:9.
故选:C.
14.解:∵OE⊥OD,
∴∠DOE=90°,
∵∠ODE=45°,
∴△DOE是等腰直角三角形,
∴OD=OE,
∴①正确;
∵四边形ABCD是正方形,
∴∠DAC=∠BAC,
∵∠DEO=90°﹣∠ODE=45°,
∴∠DAC=∠DEO=45°,
∵∠AGD=∠EGO,
∠DAC+∠AGD+∠ADE=180°,
∠DEO+∠EGO+∠AOE=180°,
∴∠ADE=∠AOE,
∴②正确;
∵四边形ABCD是正方形,
∴∠ACD=∠ACB,
∵∠ODE=45°,
∴∠ODE=∠ACD=45°,
∵∠DGO=∠DGC,
∴△GOD∽△GDC,
∴,
∴DG2=GO GC;
∴③正确;
∵四边形ABCD是正方形,AB=3,AE=1,
∴AD=CD=AB=3,
∴DE,
∵△DOE是等腰直角三角形,
∴OE=OD,
∴④正确,
∴正确结论个数为4,
故选:D.
15.解:∵AD∥BC,
∴设AD与BC之间的距离为h,
∴,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
∴△ADO∽△CBO,
∴,
故选:A.
16.解:过O点作OM∥CD,
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD=14,
∴OM是△ABD的中位线,
∴AM=DMAD,OMBA=7,
∵AF∥OM,
∴△AEF∽△MEO,
∴,
∴,
∴AE2.2,
故选:B.
17.解:∵四边形ABCD 是平行四边形,
∴AD∥BC,AB=CD,CD∥AB,
∴△CFG∽△ADG,
∴,
故A不正确;
∵CD∥AE,
∴△CDG∽△AEG,
∴,
∵AB=DC,
∴,
故B正确;
∵△BEF∽△CDF,
∴,
故C,D不正确;
故选:B.
18.解:∵平行四边形ABCD,
∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴,
∵M为AD中点,
∴,
∴BN=2DN,
∴,,
∵△MDN的面积为1,
∴S△CNB=4,S△CND=2,
∴S△BCD=S△CNB+S△CND=4+2=6,
∴S平行四边形ABCD=2S△BCD=2×6=12.
故选:A.
19.解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ABD的中位线,
∴OGAB,故①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴平行四边形ABDE是菱形,故②正确;
∵OA=OC,AG=DG,
∴OG是△ACD的中位线,
∴OG∥CD∥AB,OGCD,
∴S△ACD=4S△AOG,
∵S△AOG=S△BOG,
∴S△ACD=4S△BOG,故④正确;
连接FD,如图:
∵△ABD是等边三角形,AO平分∠BAD,BG平分∠ABD,
∴F到△ABD三边的距离相等,
∴S△BDF=S△ABF=2S△BOF=2S△DOF=S四边形ODGF,
∴S四边形ODGF=S△ABF,故③正确;
正确的是①②③④,
故选:D.
20.解:连接OD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中,
,
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM,
∴①正确;
∵四边形EBFD是菱形,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
由四边形EBFD是菱形,得:△EOB≌△FOB,
由①可知BF是OC的垂直平分线,则有△FOB≌△FCB,
∴△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误;
④∵四边形ABCD是矩形,四边形EBFD是菱形,
∴OA=OC,∠COF=∠AOE,OF=OE,
∴△AOE≌△COF(SAS),
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∵∠FCO=30°,
∴FMCM,BMCM,
∴,
∴S△FOM:S△BOF=1:4,
∵∠OGE=∠OMF,∠GOE=∠MOF,OE=OF,
∴△GEO≌△MFO(AAS),
∴S△GEO=S△MFO,
∴S△DEF=S△EFB=2S△BOF,
设S△EGO=x,则S△AOE=2x,S△BOF=4x,
S四边形DGOF=S△DEF﹣S△EGO=S△EFB﹣S△EGO=8x﹣x,
∴S△AOE:S四边形DGOF=2x:(8x﹣x)=2:7,
故④正确;
所以其中正确结论的个数为3个,
故选:C.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
