人教版六年级上册圆的面积表格式教案
图片预览

文档简介
课题 1.6《圆的面积(一)》 二备时间 上课时间
教学目标 1.了解圆的面积的含义,经历圆面积计算公式的推导过程,掌握圆面积计算公式 2.能正确运用圆的面积公式计算圆的面积,并能运用圆面积知识解决一些简单实际的问题 3.在探究圆面积公式的活动中,体会“化曲为直”的思想,初步感受极限思想
上限目标 运用圆面积知识解决一些实际的问题
下限目标 掌握圆面积计算公式
教学重点 圆面积计算公式的推导过程
教学难点 圆面积计算公式的推导过程
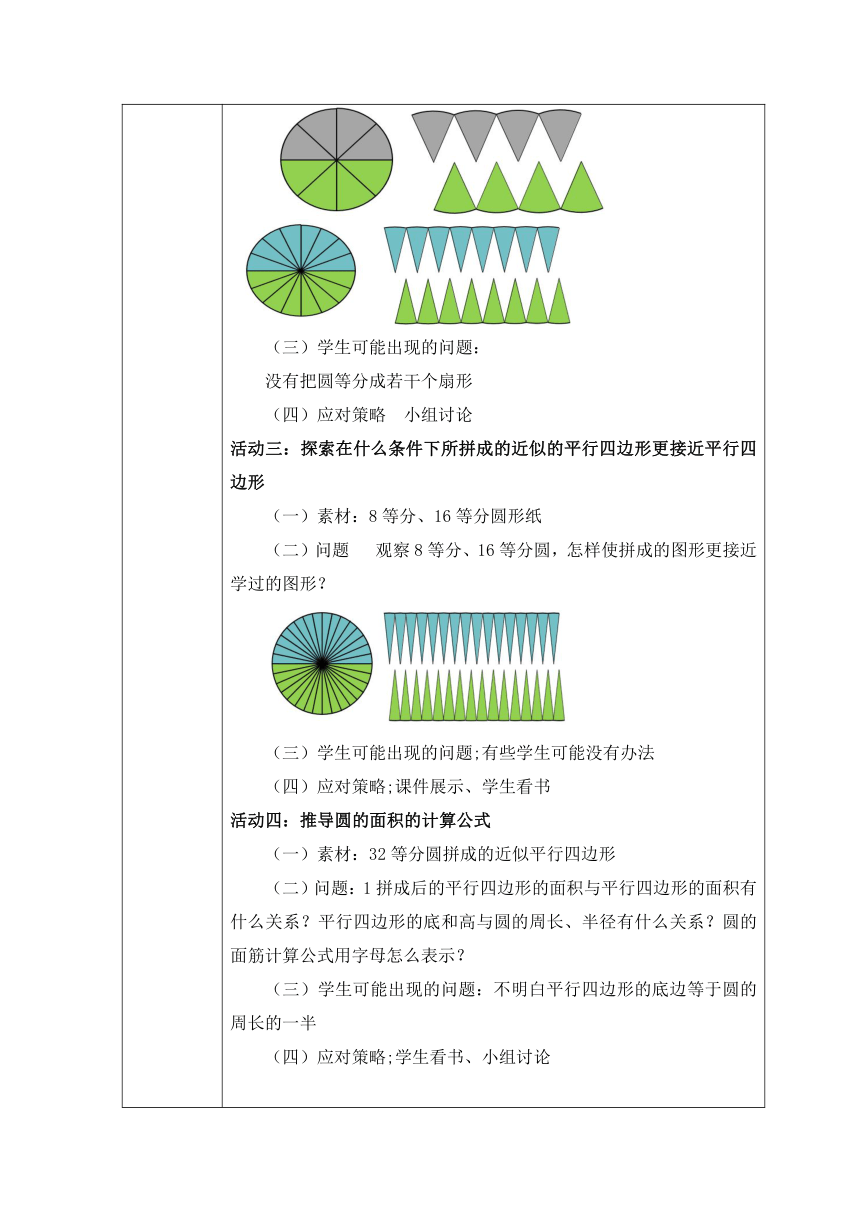
教学过程 活动一:用度量方法得到圆的面积的近似值 (一)素材:圆形纸片、课件 (二)问题:1.什么是圆的面积?动手摸一摸。2.如何得到一个圆面积?想一想,与同伴交流。 (三)学生可能出现的问题: 1.把圆的周长当成圆的面积 2.比圆内正方形大一些,剩下的怎么办? 3.把圆放在方格纸上,不是整格的怎么办? 4.比圆外正方形小一些,多的怎么办? 5.圆内画三角形。 活动二:把圆等分拼成近似的长方形 (一)素材:圆形纸片 (二)问题: 1平行四边形的面积公式是如何推导的? 2.能否把圆转化成以前学过的图形呢?3.圆可以转化成什么图形来推导面积公式?4.小组内商量,想拼成什么图形?打算怎么剪拼? (三)学生可能出现的问题: 没有把圆等分成若干个扇形 (四)应对策略 小组讨论 活动三:探索在什么条件下所拼成的近似的平行四边形更行四边形 (一)素材:8等分、16等分圆形纸 (二)问题 观察8等分、16等分圆,怎样使拼成的图形更接近学过的图形? (三)学生可能出现的问题;有些学生可能没有办法 (四)应对策略;课件展示、学生看书 活动四:推导圆的面积的计算公式 (一)素材:32等分圆拼成的近似平行四边形 (二)问题:1拼成后的平行四边形的面积与平行四边形的面积有什么关系?平行四边形的底和高与圆的周长、半径有什么关系?圆的面筋计算公式用字母怎么表示? (三)学生可能出现的问题:不明白平行四边形的底边等于圆的周长的一半 (四)应对策略;学生看书、小组讨论 习题设计: 1.判断 (1)圆的半径越大, 面积就越大。 ( √ ) (2) 一个圆的半径是2dm,它的周长与面积相等。 ( × ) (3) 圆的周长相等,面积也一定相等。 ( √ ) (4)在一个大圆内减去一个小圆就形成 了一个圆环。 ( √ ) (5)两个圆的半径之比是1∶2,面积之比也是1∶2。 ( × ) (6)一个圆的直径扩大2倍,它的面积就扩大2倍。 ( × ) 2.求圆的面积。 3.14×(6÷2) =28.26(cm ) 3.14×2 =12.56(cm ) 3.如图,把一个圆分成若干等份后,还可以拼成近似的长方形。拼成的图形与原来的圆之间有什么联系?推导一下圆的面积计算公式。 板书设计:
课后反思
教学目标 1.了解圆的面积的含义,经历圆面积计算公式的推导过程,掌握圆面积计算公式 2.能正确运用圆的面积公式计算圆的面积,并能运用圆面积知识解决一些简单实际的问题 3.在探究圆面积公式的活动中,体会“化曲为直”的思想,初步感受极限思想
上限目标 运用圆面积知识解决一些实际的问题
下限目标 掌握圆面积计算公式
教学重点 圆面积计算公式的推导过程
教学难点 圆面积计算公式的推导过程
教学过程 活动一:用度量方法得到圆的面积的近似值 (一)素材:圆形纸片、课件 (二)问题:1.什么是圆的面积?动手摸一摸。2.如何得到一个圆面积?想一想,与同伴交流。 (三)学生可能出现的问题: 1.把圆的周长当成圆的面积 2.比圆内正方形大一些,剩下的怎么办? 3.把圆放在方格纸上,不是整格的怎么办? 4.比圆外正方形小一些,多的怎么办? 5.圆内画三角形。 活动二:把圆等分拼成近似的长方形 (一)素材:圆形纸片 (二)问题: 1平行四边形的面积公式是如何推导的? 2.能否把圆转化成以前学过的图形呢?3.圆可以转化成什么图形来推导面积公式?4.小组内商量,想拼成什么图形?打算怎么剪拼? (三)学生可能出现的问题: 没有把圆等分成若干个扇形 (四)应对策略 小组讨论 活动三:探索在什么条件下所拼成的近似的平行四边形更行四边形 (一)素材:8等分、16等分圆形纸 (二)问题 观察8等分、16等分圆,怎样使拼成的图形更接近学过的图形? (三)学生可能出现的问题;有些学生可能没有办法 (四)应对策略;课件展示、学生看书 活动四:推导圆的面积的计算公式 (一)素材:32等分圆拼成的近似平行四边形 (二)问题:1拼成后的平行四边形的面积与平行四边形的面积有什么关系?平行四边形的底和高与圆的周长、半径有什么关系?圆的面筋计算公式用字母怎么表示? (三)学生可能出现的问题:不明白平行四边形的底边等于圆的周长的一半 (四)应对策略;学生看书、小组讨论 习题设计: 1.判断 (1)圆的半径越大, 面积就越大。 ( √ ) (2) 一个圆的半径是2dm,它的周长与面积相等。 ( × ) (3) 圆的周长相等,面积也一定相等。 ( √ ) (4)在一个大圆内减去一个小圆就形成 了一个圆环。 ( √ ) (5)两个圆的半径之比是1∶2,面积之比也是1∶2。 ( × ) (6)一个圆的直径扩大2倍,它的面积就扩大2倍。 ( × ) 2.求圆的面积。 3.14×(6÷2) =28.26(cm ) 3.14×2 =12.56(cm ) 3.如图,把一个圆分成若干等份后,还可以拼成近似的长方形。拼成的图形与原来的圆之间有什么联系?推导一下圆的面积计算公式。 板书设计:
课后反思
