华东师大版数学八年级上册13.2 三角形全等的判定 课堂提升训练(含解析)
文档属性
| 名称 | 华东师大版数学八年级上册13.2 三角形全等的判定 课堂提升训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 609.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 00:00:00 | ||
图片预览




文档简介
2022-2023学年度华东师大版八年级数学上册
课堂提升训练
第13章 全等三角形
13.2 三角形全等的判定
知识点1 全等三角形及相关概念
1.(2022福建龙岩月考)已知,如图,两个三角形全等,则∠1等于( )
A.73° B.57° C.50° D.60°
2.一个三角形的三条边的长分别是3,5,7,另一个三角形的三条边的长分别是3,3x-2y,x+2y.若这两个三角形全等,则x,y的值分别是 .
3.如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1)线段DE,CE,BC有怎样的数量关系 请说明理由;
(2)请你猜想△ADE中∠AED满足什么条件时,DE∥BC,并证明.
知识点2 利用“边角边(S.A.S.)”判定三角形全等
4.(教材P65变式题)如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),由三角形全等可知,工件内槽宽AB=A'B',那么判定△OAB≌△OA'B'的理由是 .
5.(2022湖北武汉蔡甸期中)如图,△ABC中,AB=8,AC=6,AD是BC边上的中线,则AD长的取值范围是 .
6.(2022湖北鄂州梁子湖期中)如图,B,C,E,F在同一直线上,AC∥DE,AC=DE,BE=CF,求证:AB∥DF.
7.(2022北京海淀外国语实验学校期中)如图,大小不同的直角△ABC和直角△DEC的直角顶点重合在点C处,AC=BC,DC=EC,连结AE、BD,点A恰好在线段BD上.
(1)找出图中的全等三角形,并说明理由;
(2)当AD=AB=4 cm时,AE= cm;
(3)猜想AE与BD的位置关系,并说明理由.
知识点3 利用“角边角(A.S.A.)”或“角角边(A.A.S.)”判定三角形全等
8.(教材P70变式题)如图,已知∠1=∠2,要使△ABE≌△ACE(A.S.A.),还需添加的条件是 .
9.(2022北京海淀外国语实验学校期中)如图,△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E,AB=10,AC=6,则BE的长为 .
10.(2022福建福州十九中期中)如图,△ABC与△DEF中,B、E、C、F在同一条直线上,BE=CF,∠A=∠D,AC∥DF,求证:AC=DF.
11.(2022独家原创)如图,E、C、B在同一条直线上,AC∥DE,∠CFB=∠ABF+∠CBF,AB=BD.求证:AC=BE.
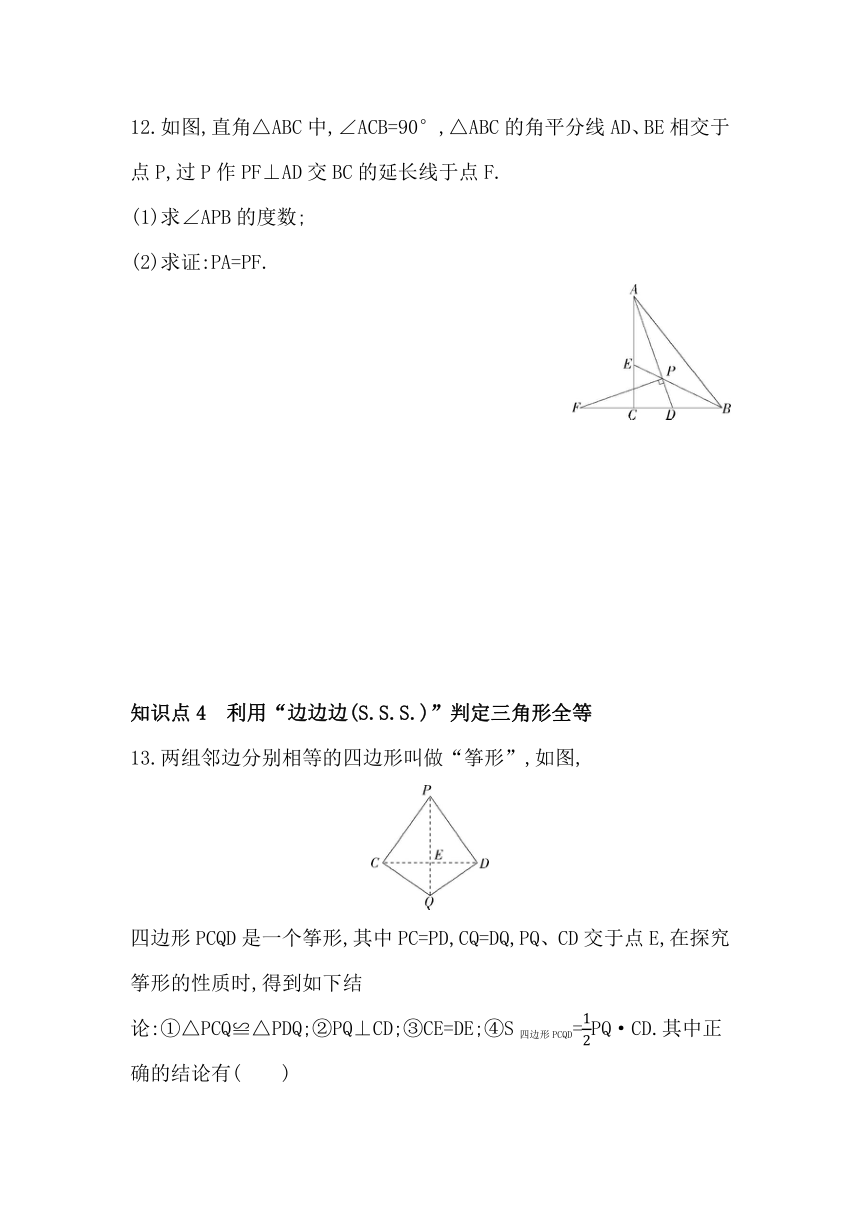
12.如图,直角△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F.
(1)求∠APB的度数;
(2)求证:PA=PF.
知识点4 利用“边边边(S.S.S.)”判定三角形全等
13.两组邻边分别相等的四边形叫做“筝形”,如图,
四边形PCQD是一个筝形,其中PC=PD,CQ=DQ,PQ、CD交于点E,在探究筝形的性质时,得到如下结论:①△PCQ≌△PDQ;②PQ⊥CD;③CE=DE;④S四边形PCQD=PQ·CD.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
14.如图,点B、E、C、F在同一直线上,BE=CF,AB=DE,AC=DF.
求证:AC∥DF.
15.(2022独家原创)如图,点A、C、E在同一直线上,AC=DE,AB=AD,BC=CE+DE.
求证:∠ABC=∠DAE.
知识点5 利用“斜边直角边(H.L.)”判定直角三角形全等
16.已知:如图,CB=CD,分别过点B和点D作AB⊥BC,AD⊥DC,两垂线相交于点A.求证:AB=AD.
17.如图,点C、F、E、B在同一条直线上,AE⊥BC,DF⊥BC,BF=CE,AB=CD.求证:AB∥CD.
18.(2022福建福州一中期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,F在AC上,BD=DF.求证:
(1)CF=EB;
(2)∠CBA+∠AFD=180°.
能力提升全练
19.(2022河南方城期中,3,)如图,∠C=∠D=90°,添加一个条件,可使用“H.L.”判定Rt△ABC与Rt△ABD全等,以下给出的条件适合的是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
20.(2021重庆中考A卷,7,)如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D
C.AC=DF D.AC∥FD
21.(2022湖北麻城期中,10,)如图,∠BAC=∠DAM,AB=AN,AD=AM,且∠ANM=60°,则∠B= .
22.(2021吉林中考,17,)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:AD=AE.
23.(2021福建中考,18,)如图,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
素养探究全练
24.[逻辑推理](2022吉林长春外国语学校期中)
如图1,△ABC 中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E.
图1 图2 图3
(1)△ABD与△CAE全等吗 BD与DE+CE相等吗 请说明理由;
(2)当直线AE绕点A旋转到如图2所示的位置(BD(3)当直线AE绕点A旋转到如图3所示的位置(BD>CE)时,其余条件不变,则BD与DE、CE的关系如何 (只需回答结论)
答案全解全析
基础过关全练
1.C 如图所示,∵两个三角形全等,∴∠3=57°,∴∠1=∠2=180°-73°-57°=50°.故选C.
2.3,2或3,1
解析 由题意得或
解得或
3.解析 (1)DE=CE+BC.
理由:∵△ABC≌△DAE,
∴AE=BC,DE=AC.
∵A,E,C三点在同一直线上,
∴AC=AE+CE,
∴DE=CE+BC.
(2)猜想:当△ADE满足∠AED=90°时,DE∥BC.
证明:∵△ABC≌△DAE,
∴∠AED=∠C,
若DE∥BC,则∠DEC=∠C,
∴∠AED=∠DEC.
又∵∠AED+∠DEC=180°,
∴∠AED=∠DEC=90°,
∴当△ADE满足∠AED=90°时,DE∥BC.
4.S.A.S.
解析 ∵点O分别是AA'、BB'的中点,
∴OA=OA',OB=OB',
在△OAB和△OA'B'中,
∴△OAB≌△OA'B'(S.A.S.).
5.1解析 如图,延长AD到点E,使ED=AD,则AE=2AD,连结CE,
∵AD是△ABC的中线,
∴CD=BD,
在△ECD和△ABD中,
∴△ECD≌△ABD(S.A.S.),
∴EC=AB=8,
∵AC=6,且EC-AC∴8-6<2AD<8+6,解得16.证明 ∵BE=CF,
∴BC+CE=FE+CE,∴BC=FE,
∵AC∥DE,∴∠ACE=∠DEC,
∵∠ACB+∠ACE=∠DEC+∠DEF=180°,
∴∠ACB=∠DEF,
又∵AC=DE,∴△ACB≌△DEF(S.A.S.),
∴∠B=∠F,∴AB∥DF.
7.解析 (1)△CBD≌△CAE,理由如下:
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△CBD与△CAE中,
∴△CBD≌△CAE(S.A.S.).
(2)∵△CBD≌△CAE,
∴AE=BD=AD+AB=4+4=8(cm),故答案为8.
(3)AE⊥BD,理由如下:
如图,设AE与CD相交于点O,
∵△CBD≌△CAE,
∴∠ADO=∠CEO,又∵∠AOD=∠COE,
∴∠OAD=∠OCE=90°,
∴AE⊥BD.
8.∠BAE=∠CAE
解析 ∵要根据A.S.A.判定全等,
∴要找到两角及其夹边分别相等,已知∠1=∠2,
∴∠AEB=∠AEC,又AE为公共边,
∴添加∠BAE=∠CAE,使△ABE≌△ACE(A.S.A.).
9.4
解析 ∵AD平分∠CAB,∴∠EAD=∠CAD,
∵DE⊥AB,∴∠DEA=∠C=90°,
在△ADE和△ADC中,
∴△ADE≌△ADC(A.A.S.),
∴AE=AC=6,
∴BE=AB-AE=10-6=4.
10.证明 ∵AC∥DF,
∴∠ACB=∠DFE,
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(A.A.S.),
∴AC=DF.
11.证明 ∵AC∥DE,∴∠ACB=∠E.
∵∠CFB=∠ABF+∠CBF,∠CFB=∠A+∠ABF,
∴∠A=∠CBF.
在△ABC和△BDE中,
∴△ABC≌△BDE(A.A.S.),
∴AC=BE.
12.解析 (1)在△ABC中,∵∠ACB=90°,
∴∠BAC+∠ABC=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=(∠BAC+∠ABC)=45°,
∴∠APB=135°.
(2)证明:∵∠APB=135°,∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,∴∠APB=∠FPB,
∵BE平分∠ABC,∴∠ABP=∠FBP.在△ABP和△FBP中,
∴△ABP≌△FBP(A.S.A.),
∴PA=PF.
13.D 在△PCQ与△PDQ中,
∴△PCQ≌△PDQ(S.S.S.),故①正确;
∵△PCQ≌△PDQ,
∴∠CPQ=∠DPQ,
在△CPE和△DPE中,
∴△CPE≌△DPE(S.A.S.),
∴CE=DE,∠PEC=∠PED,
∵∠PEC+∠PED=180°,
∴∠PEC=∠PED=90°,∴PQ⊥CD,
故②③正确;
∵PQ⊥CD,∴S四边形PCQD=S△PCQ+S△PDQ=PQ·CE+PQ·DE=PQ(CE+DE)=PQ·CD,故④正确.故选D.
14.证明 ∵BE=CF,∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(S.S.S.),∴∠ACB=∠F,
∴AC∥DF.
15.证明 ∵AC=DE,AE=AC+CE,∴AE=DE+CE.
又∵BC=CE+DE,∴BC=AE.
在△ABC和△DAE中,
∴△ABC≌△DAE(S.S.S.),∴∠ABC=∠DAE.
16.证明 连结AC,如图:
∵AB⊥BC,AD⊥CD,∴∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(H.L.),∴AB=AD.
17.证明 ∵AE⊥BC,DF⊥BC,∴∠DFC=∠AEB=90°.∵BF=CE,∴BF-EF=CE-EF,即BE=CF.
在Rt△ABE与Rt△DCF中,
∴Rt△ABE≌Rt△DCF(H.L.),
∴∠B=∠C,∴AB∥CD.
18.证明 (1)∵DE⊥AB,∴∠AED=90°=∠C,∵AD平分∠BAC,∴∠EAD=∠CAD,在△EAD和△CAD中,∴△EAD≌△CAD(A.A.S.),
∴CD=ED,在Rt△CDF和Rt△EDB中,
∴Rt△CDF≌Rt△EDB(H.L.),∴CF=EB.
(2)∵Rt△CDF≌Rt△EDB,∴∠CBA=∠CFD,
∵∠AFD+∠CFD=180°,
∴∠CBA+∠AFD=180°.
能力提升全练
19.A 根据题意可知∠C=∠D=90°,AB=AB,AB是斜边,若用H.L.判定两个三角形全等,则需给出两直角三角形的一直角边对应相等,故可添加条件AC=AD或BC=BD,故选A.
20.C ∵BF=EC,∴BF+FC=EC+FC,∴BC=EF.
当添加条件AB=DE时,△ABC≌△DEF(S.A.S.),选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(A.A.S.),选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,∠ACB=∠DFE,故△ABC≌△DEF(A.S.A.),选项D不符合题意.
故选C.
21.60°
解析 ∵∠BAC=∠DAM,∴∠BAC-∠CAD=∠DAM-∠CAD,即∠BAD=∠NAM,
在△ABD与△ANM中,
∴△ABD≌△ANM(S.A.S.),
∴∠B=∠ANM=60°.
22.证明 在△ABE与△ACD中,
∴△ABE≌△ACD(A.S.A.),∴AD=AE.
23.证明 ∵DE⊥AC,DF⊥AB,∴∠BFD=∠CED=90°,
在△BDF和△CDE中,
∴△BDF≌△CDE(S.A.S.),∴∠B=∠C.
素养探究全练
24.解析 (1)△ABD≌△CAE,BD=DE+CE.理由如下:
∵∠BAC=90°,∴∠BAD+∠CAE=90°,
∵CE⊥AE,∴∠ACE+∠CAE=90°,
∴∠ACE=∠BAD.
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠CEA=90°,
在△ABD和△CAE中,
∴△ABD≌△CAE(A.A.S.),
∴BD=AE,AD=CE,
∵AE=DE+AD,∴BD=DE+CE.
(2)BD=DE-CE.详解:
∵∠BAC=90°,∴∠BAD+∠CAE=90°,
∵CE⊥AE,∴∠ACE+∠CAE=90°,
∴∠ACE=∠BAD,
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠CEA=90°,
在△ABD和△CAE中,
∴△ABD≌△CAE(A.A.S.),
∴BD=AE,AD=CE,
∵DE=AE+AD,
∴DE=CE+BD,即BD=DE-CE.
(3)BD=DE-CE.
课堂提升训练
第13章 全等三角形
13.2 三角形全等的判定
知识点1 全等三角形及相关概念
1.(2022福建龙岩月考)已知,如图,两个三角形全等,则∠1等于( )
A.73° B.57° C.50° D.60°
2.一个三角形的三条边的长分别是3,5,7,另一个三角形的三条边的长分别是3,3x-2y,x+2y.若这两个三角形全等,则x,y的值分别是 .
3.如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1)线段DE,CE,BC有怎样的数量关系 请说明理由;
(2)请你猜想△ADE中∠AED满足什么条件时,DE∥BC,并证明.
知识点2 利用“边角边(S.A.S.)”判定三角形全等
4.(教材P65变式题)如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),由三角形全等可知,工件内槽宽AB=A'B',那么判定△OAB≌△OA'B'的理由是 .
5.(2022湖北武汉蔡甸期中)如图,△ABC中,AB=8,AC=6,AD是BC边上的中线,则AD长的取值范围是 .
6.(2022湖北鄂州梁子湖期中)如图,B,C,E,F在同一直线上,AC∥DE,AC=DE,BE=CF,求证:AB∥DF.
7.(2022北京海淀外国语实验学校期中)如图,大小不同的直角△ABC和直角△DEC的直角顶点重合在点C处,AC=BC,DC=EC,连结AE、BD,点A恰好在线段BD上.
(1)找出图中的全等三角形,并说明理由;
(2)当AD=AB=4 cm时,AE= cm;
(3)猜想AE与BD的位置关系,并说明理由.
知识点3 利用“角边角(A.S.A.)”或“角角边(A.A.S.)”判定三角形全等
8.(教材P70变式题)如图,已知∠1=∠2,要使△ABE≌△ACE(A.S.A.),还需添加的条件是 .
9.(2022北京海淀外国语实验学校期中)如图,△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E,AB=10,AC=6,则BE的长为 .
10.(2022福建福州十九中期中)如图,△ABC与△DEF中,B、E、C、F在同一条直线上,BE=CF,∠A=∠D,AC∥DF,求证:AC=DF.
11.(2022独家原创)如图,E、C、B在同一条直线上,AC∥DE,∠CFB=∠ABF+∠CBF,AB=BD.求证:AC=BE.
12.如图,直角△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F.
(1)求∠APB的度数;
(2)求证:PA=PF.
知识点4 利用“边边边(S.S.S.)”判定三角形全等
13.两组邻边分别相等的四边形叫做“筝形”,如图,
四边形PCQD是一个筝形,其中PC=PD,CQ=DQ,PQ、CD交于点E,在探究筝形的性质时,得到如下结论:①△PCQ≌△PDQ;②PQ⊥CD;③CE=DE;④S四边形PCQD=PQ·CD.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
14.如图,点B、E、C、F在同一直线上,BE=CF,AB=DE,AC=DF.
求证:AC∥DF.
15.(2022独家原创)如图,点A、C、E在同一直线上,AC=DE,AB=AD,BC=CE+DE.
求证:∠ABC=∠DAE.
知识点5 利用“斜边直角边(H.L.)”判定直角三角形全等
16.已知:如图,CB=CD,分别过点B和点D作AB⊥BC,AD⊥DC,两垂线相交于点A.求证:AB=AD.
17.如图,点C、F、E、B在同一条直线上,AE⊥BC,DF⊥BC,BF=CE,AB=CD.求证:AB∥CD.
18.(2022福建福州一中期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,F在AC上,BD=DF.求证:
(1)CF=EB;
(2)∠CBA+∠AFD=180°.
能力提升全练
19.(2022河南方城期中,3,)如图,∠C=∠D=90°,添加一个条件,可使用“H.L.”判定Rt△ABC与Rt△ABD全等,以下给出的条件适合的是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
20.(2021重庆中考A卷,7,)如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠A=∠D
C.AC=DF D.AC∥FD
21.(2022湖北麻城期中,10,)如图,∠BAC=∠DAM,AB=AN,AD=AM,且∠ANM=60°,则∠B= .
22.(2021吉林中考,17,)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:AD=AE.
23.(2021福建中考,18,)如图,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
素养探究全练
24.[逻辑推理](2022吉林长春外国语学校期中)
如图1,△ABC 中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E.
图1 图2 图3
(1)△ABD与△CAE全等吗 BD与DE+CE相等吗 请说明理由;
(2)当直线AE绕点A旋转到如图2所示的位置(BD
答案全解全析
基础过关全练
1.C 如图所示,∵两个三角形全等,∴∠3=57°,∴∠1=∠2=180°-73°-57°=50°.故选C.
2.3,2或3,1
解析 由题意得或
解得或
3.解析 (1)DE=CE+BC.
理由:∵△ABC≌△DAE,
∴AE=BC,DE=AC.
∵A,E,C三点在同一直线上,
∴AC=AE+CE,
∴DE=CE+BC.
(2)猜想:当△ADE满足∠AED=90°时,DE∥BC.
证明:∵△ABC≌△DAE,
∴∠AED=∠C,
若DE∥BC,则∠DEC=∠C,
∴∠AED=∠DEC.
又∵∠AED+∠DEC=180°,
∴∠AED=∠DEC=90°,
∴当△ADE满足∠AED=90°时,DE∥BC.
4.S.A.S.
解析 ∵点O分别是AA'、BB'的中点,
∴OA=OA',OB=OB',
在△OAB和△OA'B'中,
∴△OAB≌△OA'B'(S.A.S.).
5.1
∵AD是△ABC的中线,
∴CD=BD,
在△ECD和△ABD中,
∴△ECD≌△ABD(S.A.S.),
∴EC=AB=8,
∵AC=6,且EC-AC
∴BC+CE=FE+CE,∴BC=FE,
∵AC∥DE,∴∠ACE=∠DEC,
∵∠ACB+∠ACE=∠DEC+∠DEF=180°,
∴∠ACB=∠DEF,
又∵AC=DE,∴△ACB≌△DEF(S.A.S.),
∴∠B=∠F,∴AB∥DF.
7.解析 (1)△CBD≌△CAE,理由如下:
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△CBD与△CAE中,
∴△CBD≌△CAE(S.A.S.).
(2)∵△CBD≌△CAE,
∴AE=BD=AD+AB=4+4=8(cm),故答案为8.
(3)AE⊥BD,理由如下:
如图,设AE与CD相交于点O,
∵△CBD≌△CAE,
∴∠ADO=∠CEO,又∵∠AOD=∠COE,
∴∠OAD=∠OCE=90°,
∴AE⊥BD.
8.∠BAE=∠CAE
解析 ∵要根据A.S.A.判定全等,
∴要找到两角及其夹边分别相等,已知∠1=∠2,
∴∠AEB=∠AEC,又AE为公共边,
∴添加∠BAE=∠CAE,使△ABE≌△ACE(A.S.A.).
9.4
解析 ∵AD平分∠CAB,∴∠EAD=∠CAD,
∵DE⊥AB,∴∠DEA=∠C=90°,
在△ADE和△ADC中,
∴△ADE≌△ADC(A.A.S.),
∴AE=AC=6,
∴BE=AB-AE=10-6=4.
10.证明 ∵AC∥DF,
∴∠ACB=∠DFE,
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(A.A.S.),
∴AC=DF.
11.证明 ∵AC∥DE,∴∠ACB=∠E.
∵∠CFB=∠ABF+∠CBF,∠CFB=∠A+∠ABF,
∴∠A=∠CBF.
在△ABC和△BDE中,
∴△ABC≌△BDE(A.A.S.),
∴AC=BE.
12.解析 (1)在△ABC中,∵∠ACB=90°,
∴∠BAC+∠ABC=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=(∠BAC+∠ABC)=45°,
∴∠APB=135°.
(2)证明:∵∠APB=135°,∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,∴∠APB=∠FPB,
∵BE平分∠ABC,∴∠ABP=∠FBP.在△ABP和△FBP中,
∴△ABP≌△FBP(A.S.A.),
∴PA=PF.
13.D 在△PCQ与△PDQ中,
∴△PCQ≌△PDQ(S.S.S.),故①正确;
∵△PCQ≌△PDQ,
∴∠CPQ=∠DPQ,
在△CPE和△DPE中,
∴△CPE≌△DPE(S.A.S.),
∴CE=DE,∠PEC=∠PED,
∵∠PEC+∠PED=180°,
∴∠PEC=∠PED=90°,∴PQ⊥CD,
故②③正确;
∵PQ⊥CD,∴S四边形PCQD=S△PCQ+S△PDQ=PQ·CE+PQ·DE=PQ(CE+DE)=PQ·CD,故④正确.故选D.
14.证明 ∵BE=CF,∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(S.S.S.),∴∠ACB=∠F,
∴AC∥DF.
15.证明 ∵AC=DE,AE=AC+CE,∴AE=DE+CE.
又∵BC=CE+DE,∴BC=AE.
在△ABC和△DAE中,
∴△ABC≌△DAE(S.S.S.),∴∠ABC=∠DAE.
16.证明 连结AC,如图:
∵AB⊥BC,AD⊥CD,∴∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(H.L.),∴AB=AD.
17.证明 ∵AE⊥BC,DF⊥BC,∴∠DFC=∠AEB=90°.∵BF=CE,∴BF-EF=CE-EF,即BE=CF.
在Rt△ABE与Rt△DCF中,
∴Rt△ABE≌Rt△DCF(H.L.),
∴∠B=∠C,∴AB∥CD.
18.证明 (1)∵DE⊥AB,∴∠AED=90°=∠C,∵AD平分∠BAC,∴∠EAD=∠CAD,在△EAD和△CAD中,∴△EAD≌△CAD(A.A.S.),
∴CD=ED,在Rt△CDF和Rt△EDB中,
∴Rt△CDF≌Rt△EDB(H.L.),∴CF=EB.
(2)∵Rt△CDF≌Rt△EDB,∴∠CBA=∠CFD,
∵∠AFD+∠CFD=180°,
∴∠CBA+∠AFD=180°.
能力提升全练
19.A 根据题意可知∠C=∠D=90°,AB=AB,AB是斜边,若用H.L.判定两个三角形全等,则需给出两直角三角形的一直角边对应相等,故可添加条件AC=AD或BC=BD,故选A.
20.C ∵BF=EC,∴BF+FC=EC+FC,∴BC=EF.
当添加条件AB=DE时,△ABC≌△DEF(S.A.S.),选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(A.A.S.),选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,∠ACB=∠DFE,故△ABC≌△DEF(A.S.A.),选项D不符合题意.
故选C.
21.60°
解析 ∵∠BAC=∠DAM,∴∠BAC-∠CAD=∠DAM-∠CAD,即∠BAD=∠NAM,
在△ABD与△ANM中,
∴△ABD≌△ANM(S.A.S.),
∴∠B=∠ANM=60°.
22.证明 在△ABE与△ACD中,
∴△ABE≌△ACD(A.S.A.),∴AD=AE.
23.证明 ∵DE⊥AC,DF⊥AB,∴∠BFD=∠CED=90°,
在△BDF和△CDE中,
∴△BDF≌△CDE(S.A.S.),∴∠B=∠C.
素养探究全练
24.解析 (1)△ABD≌△CAE,BD=DE+CE.理由如下:
∵∠BAC=90°,∴∠BAD+∠CAE=90°,
∵CE⊥AE,∴∠ACE+∠CAE=90°,
∴∠ACE=∠BAD.
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠CEA=90°,
在△ABD和△CAE中,
∴△ABD≌△CAE(A.A.S.),
∴BD=AE,AD=CE,
∵AE=DE+AD,∴BD=DE+CE.
(2)BD=DE-CE.详解:
∵∠BAC=90°,∴∠BAD+∠CAE=90°,
∵CE⊥AE,∴∠ACE+∠CAE=90°,
∴∠ACE=∠BAD,
∵BD⊥AE,CE⊥AE,
∴∠ADB=∠CEA=90°,
在△ABD和△CAE中,
∴△ABD≌△CAE(A.A.S.),
∴BD=AE,AD=CE,
∵DE=AE+AD,
∴DE=CE+BD,即BD=DE-CE.
(3)BD=DE-CE.
