华东师大版数学八年级上册13.3 等腰三角形 课堂提升训练(含解析)
文档属性
| 名称 | 华东师大版数学八年级上册13.3 等腰三角形 课堂提升训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 410.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 00:00:00 | ||
图片预览




文档简介
2022-2023学年度华东师大版八年级数学上册
课堂提升训练
第13章 全等三角形
13.3 等腰三角形
知识点1 等腰三角形的概念及性质
1.等腰三角形的周长为26 cm,一边长为6 cm,那么腰长为( )
A.6 cm B.10 cm
C.6 cm或10 cm D.14 cm
2.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
3.(2022河南灵宝期中)已知等腰三角形的一个内角等于50°,则它的顶角度数是 .
4.(2021黑龙江牡丹江中考)过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为 .
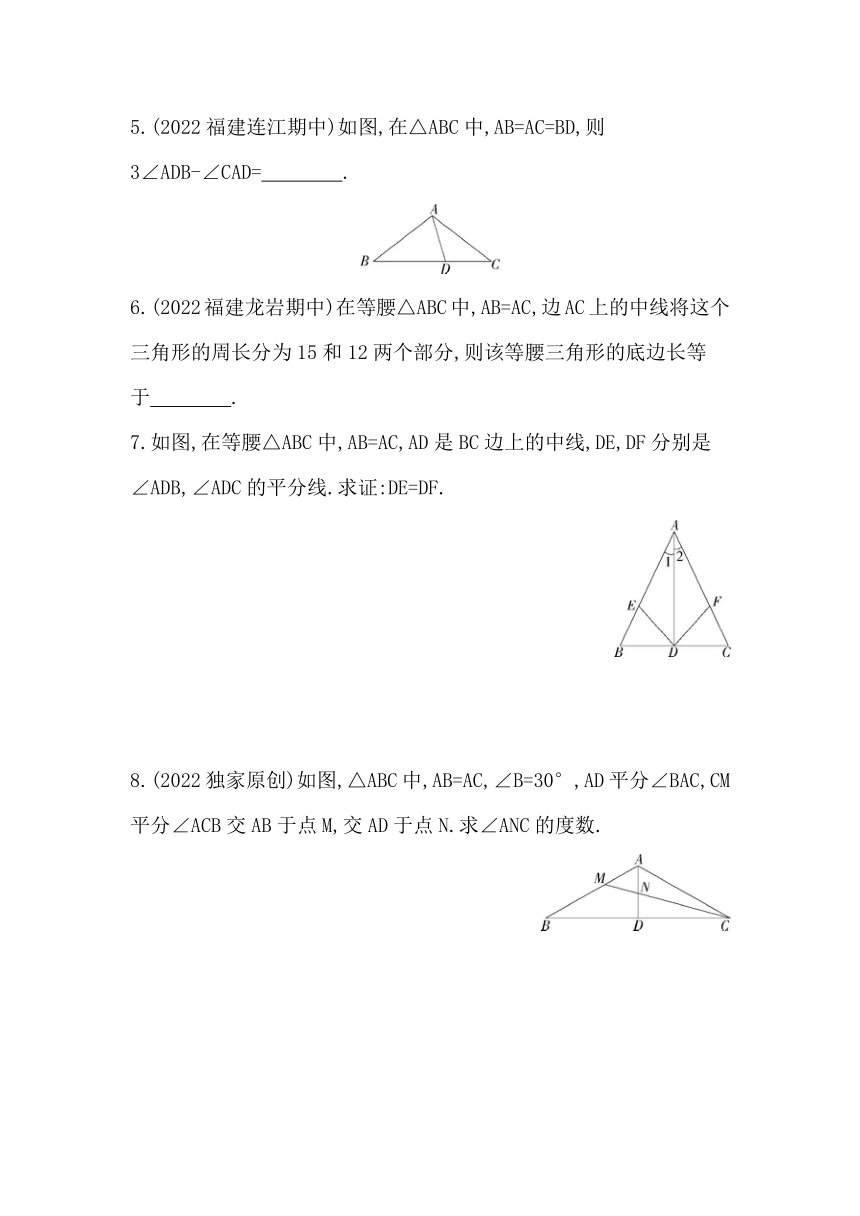
5.(2022福建连江期中)如图,在△ABC中,AB=AC=BD,则3∠ADB-∠CAD= .
6.(2022福建龙岩期中)在等腰△ABC中,AB=AC,边AC上的中线将这个三角形的周长分为15和12两个部分,则该等腰三角形的底边长等于 .
7.如图,在等腰△ABC中,AB=AC,AD是BC边上的中线,DE,DF分别是∠ADB,∠ADC的平分线.求证:DE=DF.
8.(2022独家原创)如图,△ABC中,AB=AC,∠B=30°,AD平分∠BAC,CM平分∠ACB交AB于点M,交AD于点N.求∠ANC的度数.
知识点2 等边三角形的性质
9.(2022黑龙江哈工大附中期末)如图,△ABC是等边三角形,点D在AC边上,∠DBC=40°,则∠ADB的度数是( )
A.25° B.60° C.90° D.100°
10.如图是由三个等边三角形随意摆放组成的图形,则∠1+∠2+∠3的度数为( )
A.90° B.120° C.180° D.无法确定
11.(2022福建连江期中)如图,等边△ADE的顶点D恰好在等边△ABC的边BC上,AC,ED相交于点G,连结CE.
(1)求∠ECD的度数;
(2)F是ED延长线上的点,且∠FCD=∠CAD,判断CF和GF的数量关系,并证明.
知识点3 等腰三角形及等边三角形的判定
12.(2022广东东莞期末)如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则图中的等腰三角形共有( )
A.2个 B.3个 C.0个 D.1个
13.(2022河南嵩县期末)如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,则下列结论错误的是( )
A.∠CED=30° B.∠BDE=120°
C.DE=BD D.DE=AB
14.已知△ABC中,AB=AC,∠A=60°,若BC=5 cm,则AC= cm.
15.(2022独家原创)如图,已知△ABC是等边三角形,∠ADE=∠B,AC=10,CE=6.求△ADE的周长.
16.(2022甘肃庄浪期中)已知:如图,∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:△OEF是等腰三角形.
能力提升全练
17.(2021湖南益阳中考,7,)如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
18.(2021山东滨州中考,14,)如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的大小为 .
19.(2022河南息县期中,15,)如图,在△ABC中,AB=AC,点D是边AC上一点,AD=BD,BC=DC,则∠A的大小是 .
20.(2021浙江温州中考,18,)如图,BE是△ABC的角平分线,在AB上取点D,使DB=DE.
(1)求证:DE∥BC;
(2)若∠A=65°,∠AED=45°,求∠EBC的度数.
21.(2017四川内江中考,18,)如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.
求证:△BDE是等腰三角形.
素养探究全练
22.[逻辑推理](2022广东汕头潮阳期中)如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连结AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题:
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为 ,数量关系为 ;(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立 为什么
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外) 画出相应的图形,并说明理由.
图甲 图乙 图丙
答案全解全析
基础过关全练
1.B ①当6 cm为腰长时,底边长为26-6-6=14 cm,因为14>6+6,所以不能构成三角形;②当6 cm为底边长时,腰长为(26-6)÷2=10 cm,能构成三角形.故选B.
2.D ∵AB=AC,∴△ABC是等腰三角形,∵BE=CE,∴AE是底边BC上的中线,∴AE⊥BC,故工程人员这种操作方法的依据是等腰三角形“三线合一”,故选D.
3.80°或50°
解析 当50°角是一个底角时,顶角度数是180°-50°-50°=80°;当50°角是顶角时,顶角度数是50°.∴它的顶角度数是80°或50°.
4.36°或45°
解析 分两种情况讨论:
如图1,△ABC中,AB=AC,BD=AD,AC=CD.
∵AB=AC,BD=AD,AC=CD,
∴∠ABC=∠C=∠BAD,∠CDA=∠CAD,
∵∠CDA=2∠ABC,∴∠CAB=3∠ABC,
∵∠BAC+∠ABC+∠C=180°,
∴5∠ABC=180°,∴∠ABC=36°.
图1 图2
如图2,△ABC中,AB=AC,AD=BD=CD.
∵AB=AC,AD=BD=CD,
∴∠ABC=∠C=∠DAC=∠DAB,
∴∠BAC=2∠ABC,
∵∠BAC+∠ABC+∠C=180°,
∴4∠ABC=180°,∴∠ABC=45°.
综上,∠ABC=36°或45°.
5.180°
解析 ∵AB=AC,∴∠B=∠C,∵AB=BD,∴∠ADB=∠DAB,∴2∠ADB=180°-∠B=180°-∠C,又∵∠ADB=∠C+∠CAD,∴∠C=∠ADB-∠CAD,∴2∠ADB=180°-(∠ADB-∠CAD),∴3∠ADB-∠CAD=180°.
6.7或11
解析 ①当15是腰长与腰长一半的和时,AC+AC=15,解得AC=10,所以底边长=12-×10=7;
②当12是腰长与腰长一半的和时,AC+AC=12,解得AC=8,所以底边长=15-×8=11.
所以底边长为7或11.
7.证明 ∵AB=AC,AD是BC边上的中线,
∴∠ADB=∠ADC=90°,∠1=∠2,
∵DE,DF分别是∠ADB,∠ADC的平分线,
∴∠ADE=∠ADB=45°,∠ADF=∠ADC=45°,
∴∠ADE=∠ADF,
在△ADE和△ADF中,
∴△ADE≌△ADF(A.S.A.),∴DE=DF.
8.解析 ∵AB=AC,∠B=30°,∴∠ACB=∠B=30°.
∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠CDA=90°.
∵CM平分∠ACB,∴∠MCB=∠ACB=15°.
∴∠ANC=∠CDA+∠MCB=90°+15°=105°.
9.D ∵△ABC是等边三角形,∴∠C=60°,
∵∠ADB=∠DBC+∠C,∠DBC=40°,
∴∠ADB=40°+60°=100°,故选D.
10.C ∵题图中是三个等边三角形,∴∠1=180°-60°-∠ABC=120°-∠ABC,∠2=180°-60°-∠ACB=120°-∠ACB,∠3=180°-60°-∠BAC=120°-∠BAC,∵∠ABC+∠ACB+∠BAC=180°,∴∠1+∠2+∠3=360°-180°=180°,故选C.
11.解析 (1)∵△AED,△ABC都是等边三角形,
∴∠EAD=∠CAB=∠B=∠ACB=60°,AE=AD,AC=AB,∴∠EAD-∠CAD=∠CAB-∠CAD,即∠EAC=∠DAB,在△EAC和△DAB中,
∴△EAC≌△DAB(S.A.S.),
∴∠ACE=∠B=60°,∴∠ECD=∠ACE+∠ACB=120°.
(2)CF=GF.
证明:∵∠FCG=∠ACB+∠FCD=60°+∠FCD,∠FGC=∠ADG+∠CAD=60°+∠CAD,
∠FCD=∠CAD,
∴∠FCG=∠FGC,∴CF=GF.
12.B ∵AB=AC,∠A=36°,
∴△ABC是等腰三角形,∠C=∠ABC=72°.
∵BD平分∠ABC,∴∠ABD=∠DBC=36°,
∴∠A=∠ABD=36°,∴△ABD是等腰三角形.
∵∠BDC=∠A+∠ABD=36°+36°=72°=∠C,
∴△BDC是等腰三角形.
∴共有3个等腰三角形,故选B.
13.D ∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°,∠DBC=∠ABC=30°,
∵CE=CD,∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=∠BCD=30°,A正确,不符合题意;
∴∠DBC=∠DEC,∴DE=BD,C正确,不符合题意;
∴∠BDE=180°-30°-30°=120°,B正确,不符合题意;∵DE=BD,BD14.5
解析 ∵△ABC中,AB=AC,∴△ABC是等腰三角形,又∵∠A=60°,∴△ABC是等边三角形,∴AC=BC=5 cm.
15.解析 ∵△ABC是等边三角形,∴∠A=∠B=60°.
∵∠ADE=∠B,∴∠ADE=60°,
∴△ADE是等边三角形.
∵AC=10,CE=6,∴AE=AC-CE=10-6=4.
∴△ADE的周长为4×3=12.
16.证明 ∵BE=CF,∴BE+EF=CF+EF,即BF=CE,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF≌Rt△DCE(H.L.),∴∠AFB=∠DEC,
∴OE=OF,∴△OEF是等腰三角形.
能力提升全练
17.C ∵AB∥CD,
∴∠DCA+∠CAB=180°,
即∠DCE+∠ECA+∠EAC+∠EAB=180°,
∵△ACE为等边三角形,
∴∠ECA=∠EAC=60°,
∴∠EAB=180°-40°-60°-60°=20°.
故选C.
18.34°
解析 ∵AB=AD,∴∠B=∠ADB,
∵∠BAD=44°,∴∠ADB==68°,
∵AD=DC,∴∠DAC=∠C,∵∠ADB=∠C+∠DAC,
∴∠C=∠DAC=∠ADB=34°.
19.
解析 ∵AD=BD,BC=DC,∴∠A=∠ABD,∠CDB=∠CBD,设∠A=∠ABD=x,则∠CDB=∠CBD=2x,∵AB=AC,∴∠ABC=∠C=3x,在△ABC中,∠A+∠ABC+∠C=180°,即x+3x+3x=180°,
解得x=,即∠A=.
20.解析 (1)证明:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵DB=DE,∴∠DEB=∠DBE,
∴∠DEB=∠EBC,∴DE∥BC.
(2)∵DE∥BC,∴∠C=∠AED=45°,
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°-∠A-∠C=180°-65°-45°=70°.
∵BE是△ABC的角平分线,
∴∠EBC=∠ABC=35°.
21.证明 如图,∵DE∥AC,∴∠1=∠3.
∵AD平分∠BAC,∴∠1=∠2.∴∠2=∠3.
∵AD⊥BD,∴∠2+∠B=90°,∠3+∠BDE=90°.
∴∠B=∠BDE.∴BE=DE,∴△BDE是等腰三角形.
素养探究全练
22.解析 (1)①CE⊥BD;CE=BD.
②当点D在线段BC的延长线上时,①中的结论仍然成立.理由如下:
∵∠DAE=90°,∠BAC=90°,
∴∠DAE=∠BAC,∴∠DAB=∠EAC,
又AB=AC,AD=AE,∴△DAB≌△EAC,
∴CE=BD,∠ACE=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,∴∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD.
(2)如图所示,当∠BCA=45°时,CE⊥BD.
理由:过点A作AG⊥AC交CB的延长线于点G,
∵∠BCA=45°,∴∠AGC=45°,
∴AC=AG,即△ACG是等腰直角三角形,
∵∠GAD+∠DAC=90°=∠CAE+∠DAC,
∴∠GAD=∠CAE,
又∵AG=AC,DA=EA,
∴△GAD≌△CAE,
∴∠ACE=∠AGD=45°,
∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD.
课堂提升训练
第13章 全等三角形
13.3 等腰三角形
知识点1 等腰三角形的概念及性质
1.等腰三角形的周长为26 cm,一边长为6 cm,那么腰长为( )
A.6 cm B.10 cm
C.6 cm或10 cm D.14 cm
2.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
3.(2022河南灵宝期中)已知等腰三角形的一个内角等于50°,则它的顶角度数是 .
4.(2021黑龙江牡丹江中考)过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为 .
5.(2022福建连江期中)如图,在△ABC中,AB=AC=BD,则3∠ADB-∠CAD= .
6.(2022福建龙岩期中)在等腰△ABC中,AB=AC,边AC上的中线将这个三角形的周长分为15和12两个部分,则该等腰三角形的底边长等于 .
7.如图,在等腰△ABC中,AB=AC,AD是BC边上的中线,DE,DF分别是∠ADB,∠ADC的平分线.求证:DE=DF.
8.(2022独家原创)如图,△ABC中,AB=AC,∠B=30°,AD平分∠BAC,CM平分∠ACB交AB于点M,交AD于点N.求∠ANC的度数.
知识点2 等边三角形的性质
9.(2022黑龙江哈工大附中期末)如图,△ABC是等边三角形,点D在AC边上,∠DBC=40°,则∠ADB的度数是( )
A.25° B.60° C.90° D.100°
10.如图是由三个等边三角形随意摆放组成的图形,则∠1+∠2+∠3的度数为( )
A.90° B.120° C.180° D.无法确定
11.(2022福建连江期中)如图,等边△ADE的顶点D恰好在等边△ABC的边BC上,AC,ED相交于点G,连结CE.
(1)求∠ECD的度数;
(2)F是ED延长线上的点,且∠FCD=∠CAD,判断CF和GF的数量关系,并证明.
知识点3 等腰三角形及等边三角形的判定
12.(2022广东东莞期末)如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则图中的等腰三角形共有( )
A.2个 B.3个 C.0个 D.1个
13.(2022河南嵩县期末)如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,则下列结论错误的是( )
A.∠CED=30° B.∠BDE=120°
C.DE=BD D.DE=AB
14.已知△ABC中,AB=AC,∠A=60°,若BC=5 cm,则AC= cm.
15.(2022独家原创)如图,已知△ABC是等边三角形,∠ADE=∠B,AC=10,CE=6.求△ADE的周长.
16.(2022甘肃庄浪期中)已知:如图,∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:△OEF是等腰三角形.
能力提升全练
17.(2021湖南益阳中考,7,)如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
18.(2021山东滨州中考,14,)如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的大小为 .
19.(2022河南息县期中,15,)如图,在△ABC中,AB=AC,点D是边AC上一点,AD=BD,BC=DC,则∠A的大小是 .
20.(2021浙江温州中考,18,)如图,BE是△ABC的角平分线,在AB上取点D,使DB=DE.
(1)求证:DE∥BC;
(2)若∠A=65°,∠AED=45°,求∠EBC的度数.
21.(2017四川内江中考,18,)如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.
求证:△BDE是等腰三角形.
素养探究全练
22.[逻辑推理](2022广东汕头潮阳期中)如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连结AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题:
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为 ,数量关系为 ;(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立 为什么
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外) 画出相应的图形,并说明理由.
图甲 图乙 图丙
答案全解全析
基础过关全练
1.B ①当6 cm为腰长时,底边长为26-6-6=14 cm,因为14>6+6,所以不能构成三角形;②当6 cm为底边长时,腰长为(26-6)÷2=10 cm,能构成三角形.故选B.
2.D ∵AB=AC,∴△ABC是等腰三角形,∵BE=CE,∴AE是底边BC上的中线,∴AE⊥BC,故工程人员这种操作方法的依据是等腰三角形“三线合一”,故选D.
3.80°或50°
解析 当50°角是一个底角时,顶角度数是180°-50°-50°=80°;当50°角是顶角时,顶角度数是50°.∴它的顶角度数是80°或50°.
4.36°或45°
解析 分两种情况讨论:
如图1,△ABC中,AB=AC,BD=AD,AC=CD.
∵AB=AC,BD=AD,AC=CD,
∴∠ABC=∠C=∠BAD,∠CDA=∠CAD,
∵∠CDA=2∠ABC,∴∠CAB=3∠ABC,
∵∠BAC+∠ABC+∠C=180°,
∴5∠ABC=180°,∴∠ABC=36°.
图1 图2
如图2,△ABC中,AB=AC,AD=BD=CD.
∵AB=AC,AD=BD=CD,
∴∠ABC=∠C=∠DAC=∠DAB,
∴∠BAC=2∠ABC,
∵∠BAC+∠ABC+∠C=180°,
∴4∠ABC=180°,∴∠ABC=45°.
综上,∠ABC=36°或45°.
5.180°
解析 ∵AB=AC,∴∠B=∠C,∵AB=BD,∴∠ADB=∠DAB,∴2∠ADB=180°-∠B=180°-∠C,又∵∠ADB=∠C+∠CAD,∴∠C=∠ADB-∠CAD,∴2∠ADB=180°-(∠ADB-∠CAD),∴3∠ADB-∠CAD=180°.
6.7或11
解析 ①当15是腰长与腰长一半的和时,AC+AC=15,解得AC=10,所以底边长=12-×10=7;
②当12是腰长与腰长一半的和时,AC+AC=12,解得AC=8,所以底边长=15-×8=11.
所以底边长为7或11.
7.证明 ∵AB=AC,AD是BC边上的中线,
∴∠ADB=∠ADC=90°,∠1=∠2,
∵DE,DF分别是∠ADB,∠ADC的平分线,
∴∠ADE=∠ADB=45°,∠ADF=∠ADC=45°,
∴∠ADE=∠ADF,
在△ADE和△ADF中,
∴△ADE≌△ADF(A.S.A.),∴DE=DF.
8.解析 ∵AB=AC,∠B=30°,∴∠ACB=∠B=30°.
∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠CDA=90°.
∵CM平分∠ACB,∴∠MCB=∠ACB=15°.
∴∠ANC=∠CDA+∠MCB=90°+15°=105°.
9.D ∵△ABC是等边三角形,∴∠C=60°,
∵∠ADB=∠DBC+∠C,∠DBC=40°,
∴∠ADB=40°+60°=100°,故选D.
10.C ∵题图中是三个等边三角形,∴∠1=180°-60°-∠ABC=120°-∠ABC,∠2=180°-60°-∠ACB=120°-∠ACB,∠3=180°-60°-∠BAC=120°-∠BAC,∵∠ABC+∠ACB+∠BAC=180°,∴∠1+∠2+∠3=360°-180°=180°,故选C.
11.解析 (1)∵△AED,△ABC都是等边三角形,
∴∠EAD=∠CAB=∠B=∠ACB=60°,AE=AD,AC=AB,∴∠EAD-∠CAD=∠CAB-∠CAD,即∠EAC=∠DAB,在△EAC和△DAB中,
∴△EAC≌△DAB(S.A.S.),
∴∠ACE=∠B=60°,∴∠ECD=∠ACE+∠ACB=120°.
(2)CF=GF.
证明:∵∠FCG=∠ACB+∠FCD=60°+∠FCD,∠FGC=∠ADG+∠CAD=60°+∠CAD,
∠FCD=∠CAD,
∴∠FCG=∠FGC,∴CF=GF.
12.B ∵AB=AC,∠A=36°,
∴△ABC是等腰三角形,∠C=∠ABC=72°.
∵BD平分∠ABC,∴∠ABD=∠DBC=36°,
∴∠A=∠ABD=36°,∴△ABD是等腰三角形.
∵∠BDC=∠A+∠ABD=36°+36°=72°=∠C,
∴△BDC是等腰三角形.
∴共有3个等腰三角形,故选B.
13.D ∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°,∠DBC=∠ABC=30°,
∵CE=CD,∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=∠BCD=30°,A正确,不符合题意;
∴∠DBC=∠DEC,∴DE=BD,C正确,不符合题意;
∴∠BDE=180°-30°-30°=120°,B正确,不符合题意;∵DE=BD,BD
解析 ∵△ABC中,AB=AC,∴△ABC是等腰三角形,又∵∠A=60°,∴△ABC是等边三角形,∴AC=BC=5 cm.
15.解析 ∵△ABC是等边三角形,∴∠A=∠B=60°.
∵∠ADE=∠B,∴∠ADE=60°,
∴△ADE是等边三角形.
∵AC=10,CE=6,∴AE=AC-CE=10-6=4.
∴△ADE的周长为4×3=12.
16.证明 ∵BE=CF,∴BE+EF=CF+EF,即BF=CE,
在Rt△ABF和Rt△DCE中,
∴Rt△ABF≌Rt△DCE(H.L.),∴∠AFB=∠DEC,
∴OE=OF,∴△OEF是等腰三角形.
能力提升全练
17.C ∵AB∥CD,
∴∠DCA+∠CAB=180°,
即∠DCE+∠ECA+∠EAC+∠EAB=180°,
∵△ACE为等边三角形,
∴∠ECA=∠EAC=60°,
∴∠EAB=180°-40°-60°-60°=20°.
故选C.
18.34°
解析 ∵AB=AD,∴∠B=∠ADB,
∵∠BAD=44°,∴∠ADB==68°,
∵AD=DC,∴∠DAC=∠C,∵∠ADB=∠C+∠DAC,
∴∠C=∠DAC=∠ADB=34°.
19.
解析 ∵AD=BD,BC=DC,∴∠A=∠ABD,∠CDB=∠CBD,设∠A=∠ABD=x,则∠CDB=∠CBD=2x,∵AB=AC,∴∠ABC=∠C=3x,在△ABC中,∠A+∠ABC+∠C=180°,即x+3x+3x=180°,
解得x=,即∠A=.
20.解析 (1)证明:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵DB=DE,∴∠DEB=∠DBE,
∴∠DEB=∠EBC,∴DE∥BC.
(2)∵DE∥BC,∴∠C=∠AED=45°,
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°-∠A-∠C=180°-65°-45°=70°.
∵BE是△ABC的角平分线,
∴∠EBC=∠ABC=35°.
21.证明 如图,∵DE∥AC,∴∠1=∠3.
∵AD平分∠BAC,∴∠1=∠2.∴∠2=∠3.
∵AD⊥BD,∴∠2+∠B=90°,∠3+∠BDE=90°.
∴∠B=∠BDE.∴BE=DE,∴△BDE是等腰三角形.
素养探究全练
22.解析 (1)①CE⊥BD;CE=BD.
②当点D在线段BC的延长线上时,①中的结论仍然成立.理由如下:
∵∠DAE=90°,∠BAC=90°,
∴∠DAE=∠BAC,∴∠DAB=∠EAC,
又AB=AC,AD=AE,∴△DAB≌△EAC,
∴CE=BD,∠ACE=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,∴∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD.
(2)如图所示,当∠BCA=45°时,CE⊥BD.
理由:过点A作AG⊥AC交CB的延长线于点G,
∵∠BCA=45°,∴∠AGC=45°,
∴AC=AG,即△ACG是等腰直角三角形,
∵∠GAD+∠DAC=90°=∠CAE+∠DAC,
∴∠GAD=∠CAE,
又∵AG=AC,DA=EA,
∴△GAD≌△CAE,
∴∠ACE=∠AGD=45°,
∴∠BCE=∠ACB+∠ACE=90°,即CE⊥BD.
