2022-2023学年沪科版七年级数学上册1.1 正数和负数 第1课时 课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年沪科版七年级数学上册1.1 正数和负数 第1课时 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 800.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 22:14:10 | ||
图片预览




文档简介
(共19张PPT)
1.1 正数和负数
第1课时
1.通过实例,体会和认识引入负数的必要性,掌握正数和负数的概念;
2.能应用正负数表示生活中具有相反意义的量,理解“0”的意义;
3.经历借助生活中的实际情境探究的过程,培养学生应用数学知识的意识,提高分析问题和解决问题的能力;
4.通过探究培养学生的观察、归纳和概括能力,激发学生的学习兴趣.
学习目标
正数和负数
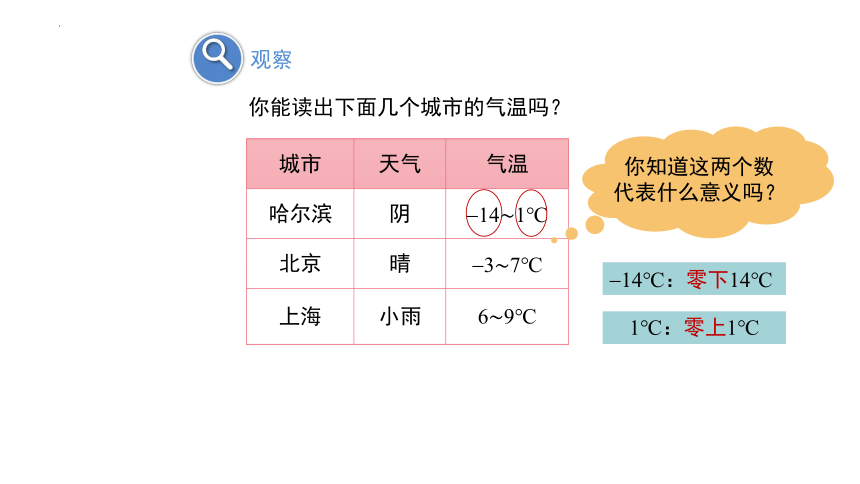
你能读出下面几个城市的气温吗?
观察
城市 天气 气温
哈尔滨 阴 141℃
北京 晴 37℃
上海 小雨 69℃
你知道这两个数代表什么意义吗?
14℃:零下14℃
1℃:零上1℃
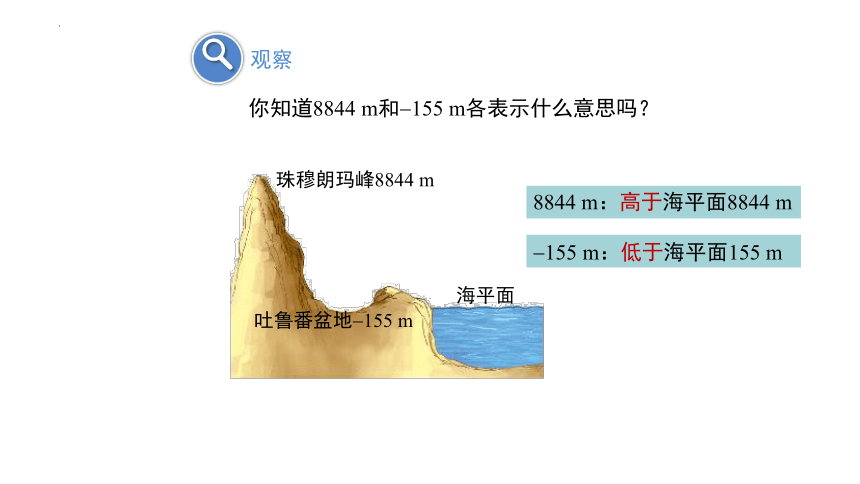
你知道8844 m和 155 m各表示什么意思吗?
观察
珠穆朗玛峰8844 m
吐鲁番盆地 155 m
海平面
8844 m:高于海平面8844 m
155 m:低于海平面155 m
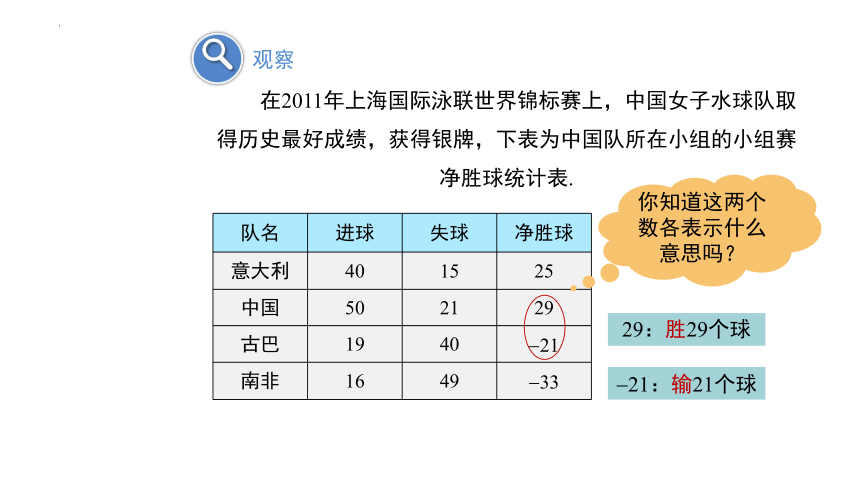
在2011年上海国际泳联世界锦标赛上,中国女子水球队取得历史最好成绩,获得银牌,下表为中国队所在小组的小组赛净胜球统计表.
观察
队名 进球 失球 净胜球
意大利 40 15 25
中国 50 21 29
古巴 19 40 21
南非 16 49 33
你知道这两个数各表示什么意思吗?
29:胜29个球
21:输21个球
某镇办4家企业今年第一季度的产值与去年同期相比的增长情况表.
观察
企业名称 面粉厂 砖瓦厂 油厂 针织厂
增长率(%) 9.2 7.3 1.5 2.8
你知道这两个数各表示什么意思吗?
7.3:增长7.3%
1.5:降低1.5%
想一想
上面出现的数中哪些是我们熟悉的数?
1,6,7,9,8844…
这样的数叫做正数.
3, 14, 155, 1.5…
这些数与上面的正数有什么不同?
在正数前面添上了负号“ ”
负数
归纳
大于0的数叫做正数.
在正数前面添上负号“”的数叫做负数.
0既不是正数,也不是负数.
正数的前面也可添上“ ”号.
(通常可省略不写)
“+”为正数的符号,
读作“正”.
“”为负数的符号,读作“负”.
+3和3读作:
正3或3
3读作:
负3
做一做
3.5
35%
26%
0
5
2.8
+3
100
正数的家
负数的家
既不是正数,也不是负数.
在计数时,数0可以表示没有,如0个.
0还常用来表示某种量的基准,例如0℃不能理解成没有温度,它是实际温度为冰点时的计量结果,用来作为计量温度的基准.
0比任何正数小,比任何负数大,它是正数与负数的分界.
思考
零下14℃
零上1℃
意义相反
都具有数量
海平面以上8844米
海平面以下155米
增长7.3%
降低1.5%
相反意义的量是成对出现的;
与一个量成相反意义的量不止一个;
相反意义的量包含两个要素:意义相反;都具有数量;
相反意义的两个量必须是同类量.
注意
相反意义的量
+
14℃
1℃
下面各组量都具有什么共同特征?
1
2
3
4
与上升2 m成相反意义的量可以是下降1 m,下降2 m…
上升与下降不是相反意义的量
节约粮食5吨与浪费钢材3吨不是相反意义的量.
做一做
如果80 m表示向东走80 m,那么 60 m表示____________.
如果80 m表示向西走80 m,那么 60 m表示____________.
如果水位升高3 m时水位变化记作+3 m,那么水位下降3 m时的水位变化记作______m.
月亮表面的白天平均温度是零上126℃,记作_______℃,夜间平均温度是零下150℃,记作_______ ℃.
向西走60 m
向东走60 m
3
+126
150
典型例题
【例】(1)与去年相比,某乡今年的水稻种植面积扩大了10 hm2(公顷),小麦的种植面积减少了5 hm2,油菜的种植面积不变,写出这三种农作物今年种植面积的增加量;
解:(1)与去年相比,该乡今年的水稻种植面积增加了10 hm2 ,小麦种植面积增加了 5 hm2 ,油菜的种植面积增加了0 hm2.
使用负数后,在表示具有相反意义的两个词语之中,只用一个词语就可以把事情说清.如减少5 hm2就可说成增加 5 hm2.
典型例题
(2)某市“12315”中心2011年国庆期间受理消费申诉件数:日用百货类比上年同期增长了10%,家用电子电器类比上年下降了20%.写出这两类消费商品申诉件数的增长率.
解:(2)与上年同期相比,消费商品申诉件数:日用百货类增长了10%,家用电子电器类增长了 20%.
你能再举出一些用正负数表示数量的实例吗?
随堂练习
1.填空:
(1)如果向东走3 km,记作+3 km,那么向西走2 km,记作 ;
(2)如图是温度计的一部分,其中温度计甲的示数为 摄氏度,记作 ℃;温度计乙的示数为 摄氏度,记作 ℃.
(3)如果将盈利1万元,记作+1万元,那么 2万元就表示 2万元.
零上5
2 km
+5
零下3
3
亏损
0
10
5
10
5
15
20
10
5
10
5
15
20
0
甲
0
10
5
10
5
15
20
10
5
10
5
15
20
0
乙
随堂练习
2.指出下列问题中的“基准”,再用正、负数表示问题中的量:
(1)某一天正午前2 h与正午后3 h;
(2)某水文站测得的水位每天下降2 cm,一天前、一天后的水位分别该如何表示?
解:(1)基准是正午(中午12:00),正午后为正,则正午前2 h记为 2 h,正午后3 h记作+3 h;
(2)选择当天水位为基准,一天后规定为负,一天前则为正.一天前水位为+2 cm,一天后水位为 2 cm.
随堂练习
4.向东行进 50 m表示的意义是( )
A. 向东行进50 m B.向南行进50 m
C.向北行进50 m D.向西行进50 m
3.下列结论中正确的是( )
A. 0既是正数,又是负数 B. 0是最小的正数
C. 0是最大的负数 D. 0既不是正数,也不是负数
D
D
正数和负数的概念:
大于0的数叫做正数.在正数前面添上负号“ ”的数叫做负数.
正数和负数
相反意义的量:
相反意义的量是成对出现的.
与一个量成相反意义的量不止一个.
相反意义的量包含两个要素:意义相反;都具有数量.
相反意义的两个量必须是同类量.
1
2
3
0的意义:
在计数时,0可以表示没有; 表示某种量的基准;
是正数和负数的分界线.
4
1
2
3
教科书第5-6页
习题1.1
第1、2、3题
再见
1.1 正数和负数
第1课时
1.通过实例,体会和认识引入负数的必要性,掌握正数和负数的概念;
2.能应用正负数表示生活中具有相反意义的量,理解“0”的意义;
3.经历借助生活中的实际情境探究的过程,培养学生应用数学知识的意识,提高分析问题和解决问题的能力;
4.通过探究培养学生的观察、归纳和概括能力,激发学生的学习兴趣.
学习目标
正数和负数
你能读出下面几个城市的气温吗?
观察
城市 天气 气温
哈尔滨 阴 141℃
北京 晴 37℃
上海 小雨 69℃
你知道这两个数代表什么意义吗?
14℃:零下14℃
1℃:零上1℃
你知道8844 m和 155 m各表示什么意思吗?
观察
珠穆朗玛峰8844 m
吐鲁番盆地 155 m
海平面
8844 m:高于海平面8844 m
155 m:低于海平面155 m
在2011年上海国际泳联世界锦标赛上,中国女子水球队取得历史最好成绩,获得银牌,下表为中国队所在小组的小组赛净胜球统计表.
观察
队名 进球 失球 净胜球
意大利 40 15 25
中国 50 21 29
古巴 19 40 21
南非 16 49 33
你知道这两个数各表示什么意思吗?
29:胜29个球
21:输21个球
某镇办4家企业今年第一季度的产值与去年同期相比的增长情况表.
观察
企业名称 面粉厂 砖瓦厂 油厂 针织厂
增长率(%) 9.2 7.3 1.5 2.8
你知道这两个数各表示什么意思吗?
7.3:增长7.3%
1.5:降低1.5%
想一想
上面出现的数中哪些是我们熟悉的数?
1,6,7,9,8844…
这样的数叫做正数.
3, 14, 155, 1.5…
这些数与上面的正数有什么不同?
在正数前面添上了负号“ ”
负数
归纳
大于0的数叫做正数.
在正数前面添上负号“”的数叫做负数.
0既不是正数,也不是负数.
正数的前面也可添上“ ”号.
(通常可省略不写)
“+”为正数的符号,
读作“正”.
“”为负数的符号,读作“负”.
+3和3读作:
正3或3
3读作:
负3
做一做
3.5
35%
26%
0
5
2.8
+3
100
正数的家
负数的家
既不是正数,也不是负数.
在计数时,数0可以表示没有,如0个.
0还常用来表示某种量的基准,例如0℃不能理解成没有温度,它是实际温度为冰点时的计量结果,用来作为计量温度的基准.
0比任何正数小,比任何负数大,它是正数与负数的分界.
思考
零下14℃
零上1℃
意义相反
都具有数量
海平面以上8844米
海平面以下155米
增长7.3%
降低1.5%
相反意义的量是成对出现的;
与一个量成相反意义的量不止一个;
相反意义的量包含两个要素:意义相反;都具有数量;
相反意义的两个量必须是同类量.
注意
相反意义的量
+
14℃
1℃
下面各组量都具有什么共同特征?
1
2
3
4
与上升2 m成相反意义的量可以是下降1 m,下降2 m…
上升与下降不是相反意义的量
节约粮食5吨与浪费钢材3吨不是相反意义的量.
做一做
如果80 m表示向东走80 m,那么 60 m表示____________.
如果80 m表示向西走80 m,那么 60 m表示____________.
如果水位升高3 m时水位变化记作+3 m,那么水位下降3 m时的水位变化记作______m.
月亮表面的白天平均温度是零上126℃,记作_______℃,夜间平均温度是零下150℃,记作_______ ℃.
向西走60 m
向东走60 m
3
+126
150
典型例题
【例】(1)与去年相比,某乡今年的水稻种植面积扩大了10 hm2(公顷),小麦的种植面积减少了5 hm2,油菜的种植面积不变,写出这三种农作物今年种植面积的增加量;
解:(1)与去年相比,该乡今年的水稻种植面积增加了10 hm2 ,小麦种植面积增加了 5 hm2 ,油菜的种植面积增加了0 hm2.
使用负数后,在表示具有相反意义的两个词语之中,只用一个词语就可以把事情说清.如减少5 hm2就可说成增加 5 hm2.
典型例题
(2)某市“12315”中心2011年国庆期间受理消费申诉件数:日用百货类比上年同期增长了10%,家用电子电器类比上年下降了20%.写出这两类消费商品申诉件数的增长率.
解:(2)与上年同期相比,消费商品申诉件数:日用百货类增长了10%,家用电子电器类增长了 20%.
你能再举出一些用正负数表示数量的实例吗?
随堂练习
1.填空:
(1)如果向东走3 km,记作+3 km,那么向西走2 km,记作 ;
(2)如图是温度计的一部分,其中温度计甲的示数为 摄氏度,记作 ℃;温度计乙的示数为 摄氏度,记作 ℃.
(3)如果将盈利1万元,记作+1万元,那么 2万元就表示 2万元.
零上5
2 km
+5
零下3
3
亏损
0
10
5
10
5
15
20
10
5
10
5
15
20
0
甲
0
10
5
10
5
15
20
10
5
10
5
15
20
0
乙
随堂练习
2.指出下列问题中的“基准”,再用正、负数表示问题中的量:
(1)某一天正午前2 h与正午后3 h;
(2)某水文站测得的水位每天下降2 cm,一天前、一天后的水位分别该如何表示?
解:(1)基准是正午(中午12:00),正午后为正,则正午前2 h记为 2 h,正午后3 h记作+3 h;
(2)选择当天水位为基准,一天后规定为负,一天前则为正.一天前水位为+2 cm,一天后水位为 2 cm.
随堂练习
4.向东行进 50 m表示的意义是( )
A. 向东行进50 m B.向南行进50 m
C.向北行进50 m D.向西行进50 m
3.下列结论中正确的是( )
A. 0既是正数,又是负数 B. 0是最小的正数
C. 0是最大的负数 D. 0既不是正数,也不是负数
D
D
正数和负数的概念:
大于0的数叫做正数.在正数前面添上负号“ ”的数叫做负数.
正数和负数
相反意义的量:
相反意义的量是成对出现的.
与一个量成相反意义的量不止一个.
相反意义的量包含两个要素:意义相反;都具有数量.
相反意义的两个量必须是同类量.
1
2
3
0的意义:
在计数时,0可以表示没有; 表示某种量的基准;
是正数和负数的分界线.
4
1
2
3
教科书第5-6页
习题1.1
第1、2、3题
再见
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
